Применение метода Брауна -Робинсона для поиска оптимальных стратегий в экономике Куликова Е.Б., Панченко О.О., Хоруженко А.С.

Источник: Актуальные вопросы современной науки – 2011 / Тезисы докладов XII международной научно-практической конференции «Актуальные вопросы современной науки». – Таганрог, Центр научной мысли – 2011, с. 176 – 179.

УДК 519.85

Применение метода Брауна -Робинсона для поиска оптимальных стратегий в экономике

Куликова Е.Б., Панченко О.О., Хоруженко А.С.

Науч. рук.: асс. Хоруженко А.С.

Донецкий национальный технический университет, г. Донецк

Введение

Распространенный способ решения матричной игры путем сведения ее к задаче линейного программирования обладает тем недостатком, что процесс решения задачи линейного программирования существенно усложняется для матриц большой размерности. В таких случаях обычно используют методы декомпозиции задачи линейного программирования, когда вместо решения задачи с исходной матрицей строится координирующая задача с матрицей, у которой мало строк, но много столбцов. На каждой итерации координирующей задачи решается некоторая совокупность вспомогательных задач линейного программирования с матрицами меньших размерностей. К сожалению, декомпозиционные методы эффективны лишь для матриц специального вида (например, блочно-диагональных).

Идея метода Брауна-Робинсона (метода фиктивного разыгрывания) многократное фиктивное разыгрывание игры с заданной матрицей выигрыша.

Одно повторение игры – партия. Пусть разыгрывается игра с – матрицей A = {a_ij}. В 1-й партии оба игрока выбирают совершенно произвольные чистые стратегии. В k-й партии каждый игрок выбирает ту чистую стратегию, которая максимизирует его ожидаемый выигрыш против наблюдаемого эмпирического вероятностного распределения противника за (k-i) партий.

Предположим, что за первые k разыгрываний игрок 1 использовал i-ю стратегию раз (i= 1, ..., m), а игрок 2 – j-ю стратегию раз (i=1, ..., n).

Тогда в (k+1)-й партии игрок 1 будет использовать -ю стратегию, а игрок 2 ‒ свою -ю стратегию, где

Пусть – значение матричной игры.

Векторы $x^k = \{ \xi_1^k/ k , \ldots , \xi_{10} ^k / k\}$ , $y^k = \{ \eta_1^k/ k , \ldots , \eta_{10} ^k / k\}$ – являются смешанными стратегиями игроков, тогда по определению значения игры имеем:

Таким образом, получен некоторый итеративный процесс, позволяющий находить приближенное решение матричной игры, при этом степень близости приближения к истинному значению игры определяется длиной интервала

Сходимость алгоритма гарантируется теоремой:

[4]

Описание объекта исследования

Пусть первый игрок – это «Конкурент», а второй – «Фирма». Стратегии игрока 1 расположены по строкам, а игрока 2 – по столбцам матрицы выигрышей. Рассмотрим алгоритм фиктивного разыгрывания на примере игры этих двух игроков (1 – «Конкурент», 2 – «Фирма») с нулевой суммой с функцией игры $H : X\times Y \rightarrow R$ , $x=(x_1 , \ldots , x_{10}), y=(y_1 , \ldots , y_{10})$ – наборы стратегий игроков [2].

Введем следующие обозначения:

i – номер критерия ,i=1 ... I_k ;

k – номер комплексного показателя , k=1,2,3; I_k – количество критериев, используемых для расчета k- го показателя;

n – количество товаров, рассматриваемых в ассортименте;

t – индекс товара , t=1..n;

V_ik – вес критерия по k-му показателю , V_ik = 1...10;

Z_ikt – значение i-го критерия по k-му показателю товара t (бальная оценка).

Фактическая оценка i-го критерия по k-му показателю товара t с учетом весовых коэффициентов:

$S_{ikt}= V_{ik}\times Z_{ikt}.$

Идеальное, т. е. максимальное или наилучшее, значение i-го критерия по k-му показателю товара t с учетом весовых коэффициентов:

$S_{ikt} ^ 0 = V_{ik}\times 10 .$

Значение k-го показателя по товару t, выраженное в процентах, рассчитывается по формуле:

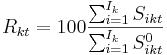$R_{kt}= 100 \frac {\sum _{i=1}^{I_k} S_{ikt}}{\sum_{i=1}^{I_k}S_{ikt}^0}$ ,

где k=1,2,3.

Разыгрывается игра с 10×10 - матрицей A = {a_ij}.

В первой партии оба игрока выбирают совершенно произвольные чистые стратегии (например, первого столбца и первой строки соответственно) [1].

Пусть векторы

$x^k = \{ \xi_1^k/ k , \ldots , \xi_{10} ^k / k\}$ , $y^k = \{ \eta_1^k/ k , \ldots , \eta_{10} ^k / k\}$ –

смешанные стратегии игроков 1 и 2 соответственно, тогда можно считать разумным следующее их поведение.

Затем игрок 1 выбирает такую чистую стратегию i из набора своих 10 стратегий x, которая максимизирует его средний выигрыш

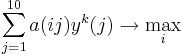$\sum_{j=1} ^{10} a(ij) y^k (j) \rightarrow \max_i$ ,

при условии, что игрок 2 использует свою смешанную стратегию y^k.

Игрок 2 выбирает такую чистую стратегию j из набора своих 10 стратегий y, которая минимизирует его средний проигрыш

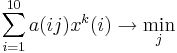- $\sum_{i=1} ^{10} a(ij) x^k (i) \rightarrow \min_j$ ,

при условии, что игрок 1 использует свою смешанную стратегию x^k.

Итак, предположим, что за первые k разыгрываний игрок 1 использовал i-ю стратегию $\xi_i^k ,$ раз $(i= 1 , \ldots , 10)$ , а игрок 2 – j-ю стратегию $\eta_j^k$ раз $(j= 1 , \ldots , 10).$ Тогда в (k+1)-й стратегии игрок 1 будет использовать i_k_{+ 1}-ю стратегию , а 2 – свою j_k _{+ 1} - ю стратегию, ν – значение матричной игры [3].

С помощью этого итеративного процесса находим приближенное решение задачи x^k и y^k .

Для визуализации моделирования данной матричной игры была разработана программа на языке C#.

Она позволяет оптимизировать процесс поиска оптимальной стратегии и является применимой для любого вида матриц.

Выводы

Благодаря разработанной программе можно легко выбрать оптимальное распределение товаров-стратегий для двух фирм: «Фирмы» и «Конкурента».

Предложенный в работе метод может быть применен в экономике для планирования товарного ассортимента фирмы, повышения спроса, обороны позиций, завоевания долей рынка, повышения производительности.

Дальнейшее развитие программы связано с проектированием функционального, интуитивно понятного и эргономичного интерфейса.

Литература

1. Губко М.В., Новиков Д.А. Теория игр в управлении организационными системами. – Москва, 2005. – 138 с.

2. http://www.wikiznanie.ru/ru-wz/index.php/Конкурентно-ценовая_стратегия_фирмы_в_условиях_олигополистической_конкуренции,_разработанная_на_основе_теории_игр [14.06.2011]

3. Крушевский А.В. Теория игр. – Киев: Объединение "Высшая школа", 1977. –216 с.

4. Петросян Л.А., Зенкевич Н.А. Теория игр. – Москва, 1998. –295 с.