Вернуться в библиотеку

ПРИМЕНЕНИЕ КЛЕТОЧНЫХ АВТОМАТОВ ДЛЯ МОДЕЛИРОВАНИЯ ДИНАМИЧЕСКИХ ПРОЦЕССОВ: ОПЫТ ДОННТУ

Автор: Аноприенко А.Я., Коноплёва А.П., Плотников Д.Ю., Малёваный Е.Ф.
Источник: Электронный архив ДонНТУ, http://ea.donntu.ru...

В статье рассматривается авторский опыт применения клеточных автоматов для моделирования различных динамических процессов. При этом описывается несколько программных реализаций моделей распространения инфекций, анализа движения транспортных и пешеходных потоков, распознавания изображений на суперкомпьютере. Анализируются перспективы дальнейших исследований.

Клеточные автоматы, впервые предложенные в качестве эффективных дискретных моделей одним из основоположников современных компьютерных технологий Дж. фон Нейманом в 40-е годы прошлого века, приобрели особую популярность начиная с 90-х годов после публикации монографии «Машины клеточных автоматов» [1] и в настоящее время широко используются в компьютерных науках, математике, физике, теоретической биологии и микромеханике. Еще Дж. Фон Нейман полагал, что «многие сложные явления, такие как самовоспроизведение, рост и развитие, морфогенез, турбулентные процессы, которые трудно моделировать с помощью дифференциальных уравнений, удастся описать с помощью клеточных автоматов» (цитируется по работе [2, с.11]). В ходе последующего развития, и особенно в 90-е годы, «в процессе осознания фундаментальной моделирующей роли клеточных автоматов произошел подлинный прорыв» [2, с.12]. Одним из апогеев этого прорыва можно считать предложенную в работе [2] парадигму клеточно-автоматной сети, лежащей в основе организации и человеческого мозга, и всей физической Вселенной. С точки зрения развития компьютерных технология актуальность клеточно-автоматных моделей в настоящее время продолжает расти по мере распространения параллельных вычислений, т.к. потенциал их параллелизации можно считать практически неисчерпаемым. Этим в первую очередь объясняется наблюдаемое в настоящее время нарастание интереса к использованию и дальнейшему развитию моделей, основанных на концепции клеточных автоматов. Об этом свидетельствует и появление ряда фундаментальных монографий на эту тему, яркими примерами которых являются работы [3] и [4]. Украинскими исследователями, в частности, в НТУУ «Киевский политехнический институт», клеточные автоматы в последние годы эффективно использовались для моделирования динамики информационных потоков и диффузии информации [5], а также – для моделирования электоральных процессов [6]. В Донецком национальном техническом университете (ДонНТУ) эпизодическое использование моделей клеточных автоматов для моделирования различных физических процессов имело место уже в 90-е годы, примером чего может быть работа [7]. С 2007 года в ДонНТУ начался новый этап исследований и разработок в области клеточных автоматов, направленный на их дальнейшее развитие в контексте постбинарного компьютинга [8-12] и использование для моделирования различных динамических процессов [13-15] в контексте поиска эффективных моделей для масштабируемого распараллеливания соответствующих вычислений. Далее кратко рассматриваются некоторые примеры таких разработок и исследований.

Моделирование стохастических процессов с ограничениями

В контексте использования клеточных автоматов для моделирования динамических процессов реального мира были разработаны программные аналоги известной игры «Жизнь», отличающиеся тем, что дополнительно было предусмотрено расширение функциональных возможностей моделей за счет введения разного рода ограничений (типа наложения на поле клеточных автоматов различных масок, задающих специфические конфигурации поля, ориентированные на реалии моделируемых процессов) и возможностей дополнительного управления процессом модклирования. При этом были реализованы и исследованы модели следующих процессов: распространение инфекции на территории государств с заданными границами и распространение лавы в вулкане с заданной конфигурацией. Для решения данных задач в исследовательских целях параллельно создавались две версии программы: ориентированная на локальное использование (реализованная на языке Borland C++ Builder) и ориентированная на Web-технологии (в виде Flash- приложения).

Рисунок 1 – Пример реализации модели распространения инфекции в странах Европы

Пример результатов моделирования вариантов развития событий в случае распространения инфекции по территории Европы показан на рис. 1. При этом на левом рисунке обозначен очаг возникновения заболевания, а на правом – результат моделирования через некоторое время. Моделировался вероятностный процесс распространения инфекции, очаг которой был расположен, например, в России. Быстрее всего инфекция в этом случае распространилась по остальной территории России. Затем она проникла в приграничные страны, а также туда, куда направлены массовые туристские потоки с низким уровнем санитарного контроля, например, в Турцию. В процессе моделирования могут задаваться и модифицироваться многочисленные параметры, например, вероятность заболевания в определенной области и уровень ее сопротивляемости инфекции [13].

Моделирования движения транспорта

Еще одним направлением исследований стало использование клеточных автоматов для моделирования транспортных и людских потоков в виртуальном городе. При этом моделируется два типа автомобилей: нормальные, которые двигаются строго согласно дорожным правилам, и аномальные, которые могут их нарушать. Для реалистичности моделирования в программу введены элементы случайности, т. е. пешеходы и водители могут ошибаться, что создает потенциальные аварийные ситуации. Данная программа может использоваться для прогнозирования и исследования реального движения транспорта и пешеходов в городе с целью предотвращения аварийных ситуаций и больших пробок.

Рисунок 2 – Пример моделирование транспортных потоков, привязанный к реалиям города Донецка в районе Донбасс-арены

Одной из важных особенностей программы явилась возможность задания моделирующего поля с наложением реальных карт городских территорий. В частности, программа была проверена в действии на примере моделирования движения машин по ул. Челюскинцев в районе Донбасс-арены (рис. 2). При этом была обеспечена возможность задания режимов работы светофоров на этом участке дороге, дорожной разметки и особенностей распределения транспортных потоков [14].

Моделирование поведения толпы

В процессе исследований было также реализовано использование клеточных автоматов для моделирования поведения толпы. При этом кроме разметки поля была также обеспечена возможность задания различных наборов правил поведения людей, что позволило моделировать различные сценарии развития движения толпы. Такое моделирование является актуальным при планировании различных массовых мероприятий, в первую очередь связанных с такими масштабными событиями как проведение в Украине Евро- 2012. На всех массовых мероприятиях должен быть четкий план действий для нейтрализации возможных беспорядков и паники. Для обоснованной разработки такого плана необходимо промоделировать все возможные (или же наиболее вероятные) сценарии развития событий и провести организационные мероприятия на местах.

Рисунок 3 – Результат моделирования поведения людей в экстренной ситуации

В качестве одного из примеров реализации таких моделей на рисунке 3 представлено моделирование эвакуации детей из детского сада во время пожара: слева показан план эвакуации детей во время пожара, а справа – модельный прогноз того, как дети будут себя вести в действительности [15].

Распознавание объектов с распараллеливанием

Для исследования возможностей распараллеливания была создана программа, реализующая доработанный авторами алгоритм GrowCut [16] для выделения объектов на изображении с помощью клеточных автоматов. Программа была реализована на обычном компьютере и параллельном суперкомпьютере. Алгоритм распознавания на базе клеточных автоматов хорошо распараллеливается и позволяет получить практически линейную зависимость ускорения работы по мере увеличения задействованных узлов суперкомпьютера.

Рисунок 4 – Результат моделирования процесса выделения заданного объекта на изображении

Моделирование процесса выделения заданного объекта на изображении проиллюстрировано на рисунке 4, где слева представлено начальное изображение, а справа – результат выделения объекта. На рисунке 5 изображен график зависимости скорости работы программы от количества узлов, а на рисунке 6 – конфигурация одного узла суперкомпьютера. В дальнейшем аналогично планируется реализовать выделение объектов на видеопоследовательностях.

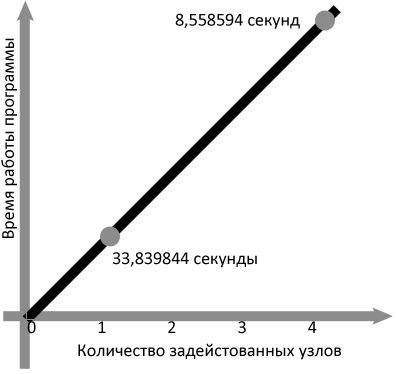
Рисунок 5 – Зависимость времени работы от количества узлов

Рисунок 6 – Конфигурация одного узла суперкомпьютера

Управляемые постбинарные клеточные автоматы

В постбинарных клеточных автоматах начальные конфигурации могут гибко и компактно задаваться в формате тетракода (т.е. кода с 4-мя состояниями). Это позволяет быстро генерировать заданное множество значений первого поколения (распределение активных клеток в начале игры) и управлять их последующим поведением в процессе моделирования на базе тетралогики (логики с 4-мя состояниями, включающими множественность и неопределенность) [8-9], что в целом позволяет реализовать целый ряд дополнительных функциональных возможностей, приближающих свойства моделируемых автоматов к особенностям реальных процессов. В числе последних можно назвать возможную недетерминированность и/или недоопределенность состояний и поведения.

Полезным нововведением является также возможность менять в процессе моделирования законы-рецепты, в том числе следующие:
- тип соседства (Мура или фон Неймана);
- условия порождения различных видов клеток;
- условия выживания и деградации клеток.

Рисунок 7 – Интерфейс программы моделирования управляемого постбинарного клеточного автомата (УПКА)

Перспективы дальнейшего развития

В дальнейшем планируется реализовать существенно более сложные модели, связанные, в частности, с моделированием погодных, климатических и экологических явлений. При этом в качестве основного вида реализуемых автоматов предполагается использовать постбинарные управляемые клеточные автоматы, реализуемые как на различных параллельных системах, в том числе на графических, так (в перспективе) и на специализированных интегральных микросхемах на базе FPGA.

Список литературы

1. Тофоли Т., Марголус Н. Машины клеточных автоматов. – М.: «Мир», 1991. – 280 с.

2. Беркович С.Я. Клеточные автоматы как модель реальности: поиски новых представлений информационных и физических процессов. – М.: Издательство МГУ, 1993. - 112 с.

3. Schiff J. L. Cellular automata: a discrete view of the world. A John Wiley&Sons inc, Publication. University of Auckland. – 2008. – 279 p.

4. Аладьев В.З. Классические однородные структуры. Клеточные автоматы. Fultus Publishing – 2009. – 535 с.

5. Ландэ Д.В. Модель диффузии информации // Информационные технологии и безопасность. Менеджмент информационной безопасности. Сборник научных трудов Института проблем регистрации информации. – Вып. 10. – 2007. – С. 51-67, http://it2b.ru/files/mdi.pdf.

6. Ландэ Д.В., Фурашев В.Н. Моделирование электоральных процессов на основе концепции клеточных автоматов // Открытые информационные и компьютерные интегрированные технологии. - Харьков: НАКУ, 2007. – Вып. 36. – С. 123-128, http://poiskbook.kiev.ua/art/x36/klet-vyb.pdf.

7. Бейгельзимер Я.Е., Спусканюк А.В., Варюхин В.Н., Эфрос Б.М. Моделирование произвольной деформации поликристаллов методом клеточных автоматов Журнал технической физики.–1998.–N11.– С. 987-998.

8. Аноприенко А.Я., Коноплева А.П. Опыт применения гиперкодов в моделировании клеточных автоматов // Научные труды Донецкого национального технического университета. Серия "Проблемы моделирования и автоматизации проектирования динамических систем" (МАП-2007). Выпуск 6 (127): Донецк: ДонНТУ, 2007. С. 220-227.

9. Аноприенко А.Я., Коноплева А.П. Развитие идеи применения гиперкодов в моделировании клеточных автоматов // Научные труды Донецкого национального технического университета. Серия: Информатика, кибернетика и вычислительная техника (ИКВТ-2008) выпуск 93: – Донецк: ДонНТУ, 2008. C. 289-316.

10. Аноприенко А.Я., Коноплева А.П., Василенко А.Ю. Оценка производительности при моделировании постбинарных клеточных автоматов и способы ее повышения // Научные труды Донецкого национального технического университета. Выпуск 147 (16). Серия «Вычислительная техника и автоматизация». – Донецк, ДонНТУ, 2009 С. 96-104.

11. Коноплева А.П., Аноприенко А.Я. Клеточные автоматы в историческом контексте и их классификация // Материалы V международной научно- технической конференции студентов, аспирантов и молодых ученых «Информатика и компьютерные технологии» – 24-26 ноября 2009 г., Донецк, ДонНТУ, 2009. С.322-329.

12. Аноприенко А. Я., Коноплева А. П. Моделирование постбинарных клеточных автоматов // Збірник наукових праць. Спеціальний випуск. Матеріали міжнародної наукової конференції «Моделювання 2010» (12-14 травня 2010 р.). Том 2., – Київ: Інститут проблем моделювання в енергетиці ім. Г.Є. Пухова. НАН України. 2010. C. 162-170.

13. Аноприенко А.Я., Плотников Д.Ю., Малёваный Е.Ф., Моделирование реальных вероятностных процессов на базе клеточных автоматов с ограничениями // Збірка матеріалів I Всеукраїнської науково-технічної конференції студентів, аспірантів та молодих вчених ІУС ТА КМ-2010.

14. Аноприенко А.Я., Плотников Д.Ю., Малёваный Е.Ф. Использование клеточных автоматов для моделирования движения транспорта. Збірка праць VI міжнародної науково-технічної конференції студентів, аспірантів та молодих науковців «Інформатика та комп’ютерні технології» 2010 р.

15. Аноприенко А.Я., Плотников Д.Ю., Моделирование поведения толпы людей на базе клеточных автоматов // Збірка матеріалів II Всеукраїнської науково-технічної конференції студентів, аспірантів та молодих вчених ІУС ТА КМ-2011.

16. GrowCut: Image cutout & matting tool, http://growcut.com.

17. Аноприенко А.Я., Коноплева А.П. Управляемые и неуправляемые постбинарные клеточные автоматы // Материалы V Всеукраинской научно- практической конференции «Современные тенденции розвития информационных технологий в науке, образовании и экономике», Луганск, 7-8 апреля 2011 г., том 1. С.19-21.