![]()
(1)
УДК 004.89, 004.94
РАЗРАБОТКА МОДЕЛИ интеллектуального ПОВЕДЕНИЯ ПЕРСОНАЖА В компьютерной ИГРЕ Robocode на основе метода нейродинамического программирования
Пocпeлов С.М., Бoндаренко И.Ю.
Донецкий национальный технический университет
кафедра прикладной математики и информатики
E-mail: pospielov@gmail.com
»сточник: —б. тр. междунар. научно-техн. конференции »нформационные управл€ющие системы и компьютерный мониторинг. Ц ƒонецк: ƒонЌ“”. Ц 2011
Аннотация:
Пocпeлов С.М., Бoндаренко И.Ю. Разработка модели поведения игрового персонажа в игре Robocode на основе метода нейродинамического программирования. В статье рассмотрена задача автоматического управления автономным агентом в динамической внешней среде на примере управления боевым роботом в компьютерной игре Robocode. Предложена модель адаптивного интеллектуального поведения боевого робота, основанная на применении нейронной сети как управляющей системы. Проведен сравнительный анализ различных алгоритмов нейродинамического программирования для обучения управляющей нейронной сети.
Введение
Повышение уровня интеллектуальности агентов в динамической внешней среде в настоящее время является одной из важнейших проблем, как для создателей автономных роботов, так и для разработчиков искусственного интеллекта в компьютерных играх. Так, одними из наиболее популярных ранее способов моделирования поведения агентов являются метод конечных автоматов и метод системы правил [1]. В динамической внешней среде персонаж может находиться в множестве различных состояний, а также может быть множество действий в этом состоянии. При этом среда также может меняться со временем. Из-за этого вышеуказанные методы слишком громоздки, требуют большого количества расчетов и сложны в разработке, не обладают механизмом самоадаптации к изменению внешней среды.
Более современным методом является метод нейродинамического программирования. Его основная идея - в аппроксимации оптимального поведения, а не в попытке точного воспроизведения (что невозможно ввиду слишком большой размерности задачи). В данной работе предлагается модернизированный метод Q-обучения с использованием обратного переигрывания. Для демонстрации этого метода выбрана игровая среда Robocode [2]. Суть этой игры заключается в создании искусственного интеллекта, управляющего игровым персонажем с целью достижения победы над персонажем противника. Данная игра имеет хорошо документированный API (application programming interfaces) с большими возможностями, что облегчит разработку персонажа. Так как все сражения происходят в реальном времени на экране монитора, то результат наших разработок будет наиболее наглядным.
Формализация игры
Задача обучения интеллектуального персонажа может быть описана при помощи Марковского процесса принятия решений (Markov decision process, MDP). В MDP агент может воспринимать множество определенных состояний среды S и выполнять действия из множества А. В любой момент времени t агент на основе текущего состояния st выбирает действие at и выполняет его. В ответ среда дает агенту вознаграждение rt=r(st,at) и переводит его в новое состояние st+1=δ(st,at). В MDP функции δ(st,at) и r(st,at) зависят только от текущего состояния и действия, и не зависят от предыдущих состояний и действий [3].
В Robocode состояния игры определяются состояниями боевых роботов, участвующих в сражении. Для определения поведения нашего персонажа нам необходима полная информация о положении нашего боевого робота на поле, состоянии его пушки и радара, а также частичная информация о найденном противнике: энергия, расстояние до противника и его скорость. Вся информация о компонентах состояния игры представлена в таблице 1.
Таблица 1 - Описание компонентов состояний игры в компьютерной игре Robocode.
|
Название компонента |
Диапазон допустимых значений |
Метод |
|
Количество энергии нашего боевого робота |
от 0 до (100+n) |
double Robot.getEnergy() |
|
Угол поворота пушки |
от 0 до 2*PI |
double Robot.getGunHeadingRadians() |
|
Перегрев пушки |
от 0 до 1-MAX_BULLET_POWER/5 |
double Robot.getGunHeat() |
|
Поворот боевого робота |
от 0 до 2*PI |
double Robot.getHeadingRadians() |
|
Оставшиеся противники |
от 0 до n |
int Robot.getOthers() |
|
Поворот радара |
от 0 до 2*PI |
double Robot.getRadarHeadingRadians() |
|
Скорость боевого робота |
от 0 до MAX_VELOCITY |
double Robot.getVelocity() |
|
Положение боевого робота по оси Х |
от 0 до BattleRules.getBattlefieldHeight() |
double Robot.getX() |
|
Положение боевого робота по оси Y |
от 0 до BattleRules.getBattlefieldWidth() |
double Robot.getY() |
|
Размер поля по оси Х |
от 400 до 5000 |
int BattleRules.getBattlefieldHeight() |
|
Размер поля по оси Y |
от 400 до 5000 |
int BattleRules.getBattlefieldWidth() |
|
Угол между положением нашего боевого робота и противника |
от -PI до PI |
double ScannedRobotEvent.getBearingRadians() |
|
Расстояние до противника |
от 0 до n |
double ScannedRobotEvent.getDistance() |
|
Количество жизней противника |
от 0 до n |
double ScannedRobotEvent.getEnergy() |
|
Поворот боевого робота противника |
от 0 до 2*PI |
double ScannedRobotEvent.getHeadingRadians() |
|
Скорость противника |
от 0 до MAX_VELOCITY |
double ScannedRobotEvent.getVelocity() |
|
Время прошедшее после нахождения противника |
от 0 до n |
long Robot.getTime()-ScannedRobotEvent.getTime() |
В каждый момент времени (такт игры) боевой робот может выполнить следующий набор действий: может двигаться, стрелять с разной силой, поворачивать себя, пушку и радар. Оптимальная последовательность этих действий, которая ведет к победе в сражении, определяет оптимальную модель поведения боевого робота. Вся информация о возможных действиях боевого робота в каждый момент времени представлена в таблице 2.
Таблица 2 - Описание действий персонажа в компьютерной игре Robocode.
|
Название параметра |
Диапазон допустимых значений |
Метод |
|
Движение боевого робота вперед |
от -MAX_VELOCITY до MAX_VELOCITY |
void AdvancedRobot.setAhead(double distance) |
|
Задать выстрел |
от MIN_BULLET_POWER до MAX_BULLET_POWER |
Bullet AdvancedRobot.setFire(double power) |
|
Сделать выстрел |
true, false |
|
|
Повернуть пушку |
от -PI до PI |
void AdvancedRobot.setTurnGunLeftRadians(double radians) |
|
Повернуть тело боевого робота |
от -PI до PI |
void AdvancedRobot.setTurnLeftRadians(double radians) |
|
Повернуть радар |
от -PI до PI |
void AdvancedRobot.setTurnRadarLeftRadians(double radians) |
В данных таблицах использованы стандартные константы, представленные в таблице 3.
Таблица 3 - Перечень констант в игре Robocode.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Скорость поворота пушки |
|
|
|
Максимальная сила выстрела |
|
|
|
Максимальная скорость поворота боевого робота |
|
|
|
Максимальная скорость боевого робота |
|
|
|
Минимальная сила выстрела |
|
|
|
Радиус охватывания радара |
|
|
|
Скорость поворота радара |
|
|
|
Бонус за врезание в противника |
|
|
|
Ущерб при столкновении с противником |
В алгоритме обучения используется вознаграждения за выполняемые действия нашего персонажа. Действия, приводящие к проигрышу в битве, имеют отрицательное вознаграждение. Все события, происходящие в игре, хранятся в памяти. В конце каждой битвы коэффициенты управляющей нейросети подстраиваются с учётом вознаграждений, полученных за выполненные действия. Перечень событий, приводящих к вознаграждениям, описан в таблице 4.
Таблица 4 - Вознаграждения в игре Robocode
|
Событие |
Награждение |
|
Попадание во врага |
FireEnergy*8 |
|
Выстрел |
-FireEnergy |
|
Столкновение со стеной |
-(abs(velocity) * 0.5 Ц 1) |
|
Столкновение с противником |
-0.6 |
|
Столкновение с противником при движении вперед |
1.2 |
Нейроалгоритм
Входными сигналами являются:
1. Вектор S={s1,s2,Еs17}, где s1,s2,Еs17 Ц свойства, определяющие текущее состояние (всего таких свойств 17 - см. табл. 1).
2. Вектор A={a1,a2,Еa6}, где a1,a2,Еa6 Ц действия, возможные для выполнения в данном состоянии (всего таких действий 6 Ц см. табл. 2).
Выходным сигналом является Y - Q-фактор, определяющий, насколько выгодна стратегия, которая начинается выполнением данного действия в текущем состоянии.
Желаемым выходным сигналом является Ỹ, вычисленный с помощью приближенного модифицированного алгоритма Q-обучения.
Нейросеть состоит из двух слоев. Число нейронов в скрытом слое является изменяемым параметром. В качестве функции активации этих нейронов была выбрана нелинейная биполярная функция Ц рациональная сигмоида вида:
|
|
(1) |
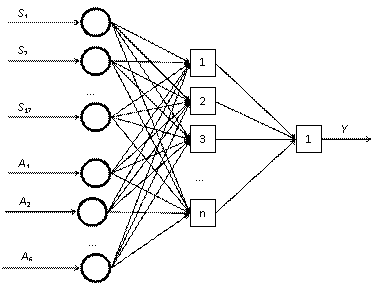
Рис. 1. Структура нейросети
Функцией ошибки является разность между Q-фактором Qreal, вычисленным нейросетью, и целевым Q-фактором Qtarget, рассчитанным с помощью модифицированного Q-алгоритма:
|
E=Qtarget Ц Qreal=Qtarget Ц Net(W,S,A) |
(2) |
Критерием качества нейросети является минимизация квадрата ошибки:
|
F(W)=(Qtarget Ц Net(W,S,A))2 → min |
(3) |
Значения весовых коэффициентов нейросети вычисляются с помощью процедуры настройки после окончания битвы алгоритмом обратного переигрывания.
Методы нейродинамического обучения
При использовании одношагового Q-обучения коррекция весов нейросети, вычисляющей Q-фактор, производится на основе оценок текущего и последующего состояний, т.е. на оценках смежных состояний. Существует два алгоритма Q-обучения Ц инкрементный и обратного переигрывания. При использовании алгоритма обратного переигрывания, обновление весов нейросети производится только после того, как агент достигнет поглощающего состояния (конец раунда в игре). В инкрементном алгоритме обновление производится после каждого шага агента (каждый такт игры). Инкрементный алгоритм является более общим, поскольку не требует обязательного наличия поглощающего состояния, но он не всегда сходится к оптимальной политике [3]. Т.к. в нашем случае у нас есть четко выраженное поглощающее состояние то целесообразней использовать алгоритм обратного переигрывания (рис. 2).
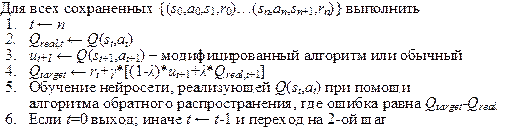
Рис. 2. Методика обратного переигрывания
Выводы
Игра Robocode показала себя хорошей средой для исследований в области нейродинамического программирования. Хорошо документированный API позволил определить основные состояния, в которых может находиться боевой робот, и действия, которые он может выполнять. Для обучения нейронной сети были выбраны вознаграждения боевого робота за его возможные действия на основе событий, происходящих в игре.
Разработанный нейроалгоритм хорошо подходит для выбранного нами алгоритма Q-обучения. Двухслойная структура нейросети позволит аппроксимировать сложную поведенческую функцию боевого робота.
Дальнейшие исследования будут посвящены разработке программной модели боевого робота, обучению нейронной сети на битвах с другими роботами, а также проверке на алгоритма на эффективность путем анализа соотношения числа побед и поражений в тестовых битвах.
1. Пocпeлов С.М., Бoндаренко И.Ю. Анализ проблем моделирования интеллектуального поведения персонажей в компьютерных играх // Сб. тр. междунар. научно-техн. конференции ЂИнформатика и компьютерные технологии 2010ї. Ц Донецк: ДонНТУ. Ц 2010
2. Robocode home [Electronic resourse] / Интернет-ресурс. - Режим доступа: URL: http://robocode.sourceforge.net/ Дата обращения: 18.03.2011.
3. Кузьмин В.В. Исследование алгоритмов обучения с подкреплением в задачах управления автономным агентом: Работа на соискание академической степени магистра компьютерных наук. Ц Рига: Рижский технический университет, 2002. Ц 65 с.