Распознавание фонем, используя TDNN
Автор: A. Waibel
Перевод: Поспелов С.М.
Оригинал: http://www.cs.toronto.edu/~hinton/absps/waibelTDNN.pdf
Нейросеть с задержкой времени разработана для распознавания фонем, характеризуется двумя важными свойствами: 1) использование 3-х слоев нейронов, иерархией, построенной так, чтобы позволять построение дискретных нелинейных плоскостей решений. TDNN запоминает эти выпуклые поверхности автоматически, используя метод обратного распространения ошибки [1]. 2) Архитектура с задержкой времени позволяет сети распознавать акустически-фонетические данные и временную зависимость между ними независимо от позиции во времени и, следовательно, не искажая временными сдвигами на входе.
Как задача было выбрано зависящее от произношения распознавание фонем «B», “D” и “G” в различных фонетических контекстах. Для сравнения, некоторые дискретные СММ были обучены для выполнения такой же задачи. Сравнительная оценка более 1946 тестовых произношений трех дикторов показала, что TDNN достигает уровня 98.5% верных ответов, в то время как уровень, показанный лучшими СММ, достиг только 93.7%. Ближайшее исследование раскрывает тот факт, что сеть «открывает» хорошо известные акустически-фонетические черты (F2-подъем, F2-спуск, гласное начало) в пригодные абстракции. Она также включает альтернативные внутренние представления для приведения разных акустических реализаций к единой концепции.
В последнее время появление новых процедур обучения и наличие высокоскоростных параллельных суперкомпьютеров вызвало возобновление интереса к коннкеционистским моделям интеллекта. Иногда также упоминающиеся, как искусственные нейронные сети или параллельно распределенные вычислительные модели, эти модели особенно интересны для познавательных задач, которые требуют удовлетворения множества условий, то есть параллельная оценка множества ключей и фактов и их интерпретация в свете многочисленных взаимосвязанных ограничений. Задачи распознавания, например, обработка речи, языка, движений, характеризуется высоким уровнем неопределенности и разнообразия, что доказывает сложность обеспечения хорошей производительности этих работ, используя стандартные последовательные методы программирования. Комплексные сети, состоящие из простых вычислительных элементов, более пригодны для таких задач не только из-за похожести на работу мозга, но и потому, что они предлагают пути для автоматического проектирования систем, позволяющих использовать несколько взаимосвязанных ограничений. В общем, такие связи слишком запутаны, чтобы быть легко программируемыми, и требуют использования стратегий автоматического обучения. Такие алгоритмы обучения сейчас существуют и были продемонстрированы в исследовании интересных внутренних абстракций в их попытках решить заданную проблему. Обучение наиболее эффективно, однако, при использовании в архитектуре, которая соответствует задаче. В действительности, применение определенных знаний в области задачи и их свойств для проектирования подходящей модели нейронной сети может оказаться ключевым элементом в успешной разработке коннкеционистских систем.
Естественно, эти техники будут очень распространены в проектировании систем автоматического распознавания речи, если окажутся успешными по сравнению с уже существующими технологиями. Липпман сравнил некоторые типы нейронных сетей с их классификаторами и оценил их способность создавать комплексные поверхности решений. Другие исследования рассмотрели актуальные задачи распознавания речи и сравнили их с психологическими данными речевого восприятия или с существующими техниками распознавания речи. Эксперименты по распознаванию речи с использованием нейросетей до сих пор главным образом были направлены на распознавание изолированных слов (наиболее – в задачах распознавания цифр) или фонетическое распознавание с предопределенным постоянным или переменным фонетическим контекстом.
Число этих исследований показывает обнадеживающую производительность распознавания, но существуют лишь немногочисленные сравнения с существующими методами. Некоторые из этих сравнений показали производительность меньше, чем у существующих методов, но другие обнаружили, что сеть обеспечивает меньшие результаты, чем другие техники. Можно утверждать, что это положение дел поощрительно в рассмотрении количества точно настроенных, что выливается в оптимизацию более популярных, созданных техник. Тем не менее, лучшие сравнительные показатели производительности нужны ранее, чем нейросети будут считаться жизнеспособной альтернативой в распознавании речи.
Одно возможное объяснение смешанных результатов производительности, получающихся до сих пор – возможно, ограничения в вычислительных ресурсах, ведущих к сокращению этой ограниченной производительности. Другое, более серьезное ограничение, однако, - неспособность большинства архитектур нейронных сетей правильно иметь дело с динамической природой речи. Два важных аспекта этого для сети есть представление временных отношений между акустическими событиями, и в то же время обеспечение неизменности при сдвиге во времени. Особое перемещение формата во времени, например, является важным сигналом для определения остановки, но это неуместно для того же положения событий, проходящих немного раньше или позже по времени. Без неизменности перемещений, нейросеть требует точного разбиения для отражения входных структур правильно. Так как это не всегда возможно практически, обучающие функции, как правило, размываются (в целях сглаживания незначительных смещений) и их производительность ухудшается. В общем, неизменность сдвигов признана критически важным свойством для коннекционистских систем, и определенное число подающих надежды моделей были предложены для областей речи и других.
В этой статье мы описываем нейросеть с задержкой времени (TDNN) , которая реализует оба этих аспекта речи и демонстрирует через обширную оцененную производительность, что лучшие результаты распознавания могут быть достигнуты, используя этот подход. В следующем разделе мы начнем с представления архитектуры и обучающей стратегии TDNN, направленной на распознавание звуков. Далее мы сравним производительность нашей TDNN-сети с наиболее популярной предшествующей техникой распознавания – Скрытыми Моделями Маркова (СММ). В разделе 3 мы начнем с описания СММ, по развитию ATR. Обе техники, СММ иTDNN, оценены по тестовой базе, и мы сообщим результаты. Мы покажем, что существенно высшая распознавательная мощность достигнута TDNN, в отличие от лучшей нашей СММ. В разделе 4 мы обратим более пристальное внимание на внутреннее представление, которому обучена TDNN для этой задачи. Она исследовала множество занимательных лингвистических образов, которые будут показаны в качестве примеров. Суть этих результатов будут далее обсуждены и подытожены в заключающем разделе этой статьи.
Чтобы быть пригодной для распознавания речи, состоящая из слоев упреждающая нейросеть должна обладать рядом свойств. Во-первых, она должна иметь несколько слоев и достаточное количество взаимосвязей между элементами в каждом слое. Это нужно для того, чтобы обеспечить возможность запоминания сетью комплексных нелинейных поверхностей решений. Во-вторых, сеть должна иметь возможность представлять заивисмость между событиями во времени. Этими событиями могут быть спектральные коэффициенты, но могут также быть и выход наивысшего уровня определяющей функции. В-третьих, важные функции или образы, заученные сетью, должны быть неизменны при временных сдвигах. В четвертых, обучающая процедура не должна требовать точных временных выравниваний для символов, которые должны запоминаться. В-пятых, количество весов в сети должно быть достаточно малым, соответственно количеству обучающих данных, поэтому сеть вынуждена кодировать обучающие данные по извлеченным закономерностям. В дальнейшем мы опишем архитектуру TDNN, которая удовлетворяет всем этим критериям, и спроектирована явно для распознавания звуков, в частности, согласных «B», «D» и «G».

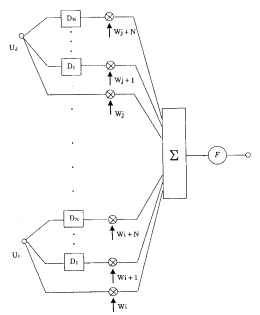
Рисунок 1. Структура TDNN
А. Архитектура TDNN для распознавания звуков.
Основной блок, используемый во многих нейросетях вычисляет взвешенную сумму входных сигналов и подаёт эту сумму на вход нелинейной функции, обычно пороговой или сигмоиде. В нашей ТDNN, этот блок модифицирован введением задержек D1 через DN. Входные сигналы J теперь будут умножены на несколько весов, один для каждой задержки и один для незадержанного ввода. Для N=2 и J=16, например, для вычисления весовой суммы 16 входных сигналов нужны будут 48 весов, причём значение каждого сигнала взято трижды в разные моменты времени. В этом случае блок ТDNN имеет способность соотносить и сравнивать текущее значения входных сигналов с историей введённых значений. В качестве нелинейной функции была выбрана сигмоида из-за своих удобных математических свойств.
Для распознавания фонем, необходимо построить трёхслойную сеть. Её общая архитектура и типичный набор действий в блоках показаны на Рис 2.
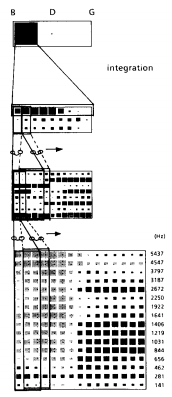
Рисунок 2. Архитектура TDNN
На самом нижнем уровне в качестве входных сигналов нейросети служат 16 нормализованных масштабированных спектральных коэффициентов. Входная речь, взятая на 12 кГц, разделена на скользящие окна и в 256-точечном FFT вычисляется каждые 5 мс. Масштабированные коэффициенты вычисляются из спектра мощности посредством вычисления входной мощности в каждой группе масштабированной мощности, где смежные коэффициенты в частоте перекрываются одним спектральным образцом и сглаживаются понижением общего образца на 50 %. Смежные временные коэффициенты сжимаются для редуцкии дальнейших данных, результированных с частотой 10 мс. Все коэффициенты входящей речи (в этом случае 15 речевых отрезков, сконцентрированные вокруг отмеченного ударного гласного) далее нормализуются. Это осуществляется вычитанием из каждого коэффициента среднего коэффициента мощности, вычисляемого по всем 15-ти отрезкам входной речи и далее нормализации каждого коэффициента с погрешностью между -1 и +1. Все речевые отрезки в нашей базе данных были приведены к одному стилю. Рис. 2 показывает результирующие коэффициенты для речевого отрезка «ВА» как входного на 8 скрытых элементов с задержкой времени, где J=16 и N=2 (то есть 16 коэффициентов на 3-х окнах задержкой времени 0, 1 и 2). Альтернативный способ представления этого изображен на рис. 2. Он показывает ввод на эти элементы с задержкой времени, расширенные пространственно в окно из 3-х частей, которое передается из входной спектрограммы. Каждый элемент в первом скрытом слое теперь получает входные данные (через 48 взвешенных связей) из коэффициентов 3-хфреймового окна. Конкретный выбор 3-х фреймов (30 мс) мотивирован предыдущими исследованиями которые предположили, что окно размером в 30 мс может достаточным для представления низкоуровневых акустически-фонетических событий для распознавания звонких согласных. Это также оптимальный выбор среди числа альтернативных конструкций, оцененных Лангом при идентичной задаче.
На втором скрытом слое каждый из 3-х элементов TDNN просматривает 5-тифреймовое окно уровней активности в 1-ом скрытом слое (т.е. J=8, N=4). Выбор большего, 5-тифреймового окна в этом слое обоснован предположением, что элементы более высокого уровня обучаются принимать решения на основе широкого временного диапазона, основывающегося на большинстве локальных образов нижних уровней.
В конце концов, выход получается посредством интеграции (суммирования) данных из каждого из 3-х элементов в скрытом слое 2 в течении времени и присоединения их к подходящему выходному элементу. На практике, это суммирование осуществляется несложно как другой нелинейный (сигмоида также отлично подойдет) элемент TDNN, который фиксирует равные веса к ряду запусков по времени в скрытом слое 2.
Когда TDNN запомнит свои внутренние представления, она выполняет распознавание посредством подачи выходной речи на элементы TDNN. По иллюстрации рис. 2 это эквивалентно передаче окон с задержкой времени на функции активации нижних уровней. На самых нижних уровнях эти функции активации состоят из сенсорных входов, т.е. из спектральных коэффициентов.
Каждый элемент TDNN, описанный в этом разделе, имеет возможность кодировать временные отношения внутри диапазона в N задержек. Более высокие уровни могут работать в больших временных промежутках, потому местные короткие признаки могут быть сформированы в нижнем слое, а более комплексные длинновременные признаки – на более высоком уровне. Процедура обучения обеспечивает то, что каждый элемент в каждом слое имеет вес, отрегулированный таким образом, который улучшает общую производительность сети.
B. Обучение в TDNN
Существуют некоторые техники обучения для оптимизации нейронных сетей. Для этой сети мы использовали метод обратного распространения ошибки. Математически, обратное распространение ошибки это градиентный спуск средней квадратичной ошибки как весовой функции. Процедура обеспечивает два прохода по сети. На протяжении прямого прохода входной образ применяется к сети со своим предыдущими силовыми связями (первоначально маленькие случайные весы). Выходы каждого нейрона на уровне вычисляются начиная с входящего и продолжается до выходного слоя. Далее выход сравнивается с желаемым и вычисляется его ошибка. На протяжении обратного прохода производная этой ошибки распространяется назад по сети и все веса корректируются так, чтобы уменьшить ошибку. Это повторяется много раз для всех тестовых произношений пока сеть не приблизится к передаче желаемого выхода.
В предыдущем разделе мы описали метод выражения временных структур в TDNN и противопоставили этот метод к обучению сети со статическим входным образом (спектрограммой), у которых результаты на чувствительной к сдвигам сети (т.е. плохая представляемость для немного неотрегулированных входных образов), также как и менее четкое решение, полученное на элементах сети (по причине неотрегулированных произношений на протяжении обучения).
Для достижения желаемой обучаемости мы должны обеспечить то, что сеть будет получать последовательность данных и она должна позволять (или способствовать) запоминанию самых мощных сигналов и последовательности сигналов в них. Концептуально, процедура обратного распространения ошибки применяется для речевых образов, распределенных по времени. Альтернативный путь для достижения этого результата – использовать пространственно расширенный входной образ, т.е., спектрограмму плюс некоторые ограничения в весах. Каждый набор элементов TDNN, описанных выше, копируется для каждого сдвига окна во времени. Таким образом, вся история деятельности доступна сразу. С момента, когда смещенные копии элементов TDNN просто дублируются, и предназначены для отслеживания одного и того же акустического события, веса соответствующих связей на сдвинутых во времени копиях должны быть ограничены, чтобы быть одинаковыми. Чтобы это осуществить, мы во-первых применяем регулярно метод обратного распространения ошибки по прямому и обратному проходу для всех сдвинутых по времени копий, будто это отдельные события. Это дает разные производные ошибки для соответствующих (сдвинутых во времени) связей. После раздельного корректирования весов для сдвинутых во времени связей, в общем, мы фактически обновляем каждый вес соответствующего соединения до одинакового значения, а именно – средним из всех соответствующих задержанных во времени весовых изменений. Рисунок 2 иллюстрирует это через отображение в каждом слое только двух связей, которые соединены (ограниченны одинаковыми значениями весов) со своими сдвинутыми во времени соседями. Конечно, это применяется ко всем связям и всем временным сдвигам. Таки образом, сеть имеет возможность выделять акустическо-фонетические образы на входе, независимо от того, где во времени они расположены. Это важное свойство, потому как оно делает сеть независимой от ошибок алгоритмов предварительной обработки, которые в другом случае понадобились бы для временного выравнивания и/или разбиения. В разделе VI-C мы покажем примеры грубо неотрегулированных образов, которые правильно распознаются благодаря этому свойству.
Процедура, описанная здесь, вычислительно более требовательная, из-за множества итераций, обязательных для запоминания комплексного многомерного пространства весов и числа обучающих образов. В нашем случае, было использовано около 800 обучающих образов, и где-то 20 000-50 000 циклов обратного распространения ошибки прошло по ходу обучения. Выполнение обучения в приемлемое время заняло 2 шага. Во первых, мы реализовали нашу обучающую процедуру на С и Фортране на 4-х процессорном суперкомпьютере Alliant. Скорость обучения могла быть значительно лучше, если бы вычисления прямого и обратного движения для нескольких разных тренировочных образов производились на параллельных или разных процессорах. Дальнейшие улучшения могут достигаться векторизацией операций и возможным сборным программированием внутренних циклов. Наше теперешнее применение достигает примерно 9-кратного ускорения на VAX 8600, но оставляет пространство для дальнейших улучшений (Ланг, для примера, сообщает об ускорении около 120 раз на 11/780 для приложения, запущенного на суперкомпьютере Convex). Второй шаг улучшения времени обучения, был дан поэтапной обучающей стратегией. В этом подходе мы начали оптимизировать сеть, основанную только на 3-х прототипных обучающих произношениях. В этом случае сходимость достигается быстро , но сеть должна запомнить представление, которое плохо обобщено для новых и разных образов. Как только достигается сходимость, сеть представляется приблизительно числом произношений и запоминанием последовательностей до сходимости.
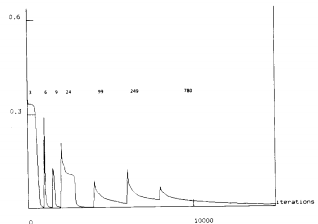
Рисунок 3. Прогресс обучения
Рис 3 показывает прогресс на протяжении типичного обучения. Измеренная ошибка равна ½ квадрата ошибки всех выходных элементов, нормализованных соответственно числу входных произношений. При этом запуске, число использовавшихся обучающих произношений было 3, 6, 9, 24, 99, 249 и 780. Как можно видеть из рис. 3, ошибка немного поднимается каждый раз, изменчивость показана в виде обучающих данных. Сеть после этого вынуждена улучшать свою представляемость, искать ключ, который обобщен лучше и ослаблять то, что в свою очередь просто не соответсвует ограниченному набору образцов. Используя полный обучающий набор из 780 произношений, этот частный запуск продолжался до итерации 35 000 (рис 3 показывает график только до 15 000 итераций). С этим полным обучающим множеством малые шаги обучения будут идти и обучаться медленно. В этом случае, используется размер шага 0.002 и момент 0.1. Подход пошагового обучения найден полезным для применения для быстрого перенесения весов сети на соседство для разумного решения, перед более медленной хорошей настройкой всех обучающих произношений.
Несмотря на эти ускорения, обучения проходит порядком на протяжении нескольких дней. Число программных уловок, также как и модификации обучающей процедуры пока еще не применены, и могут сократить время обучения в около 10 раз. Важно заметить, однако, что количество вычислений рассмотрено здесь только для обучения TDNN, но не для распознавания. Распознавание может легко производиться в более чем приемлемое время на рабочей станции или персональном компьютере. Простая структура TDNN также хорошо соответствует стандартизированному VLSI приложению. Детальные знания могут быть заучены в офф-лайне, используя существенную вычислительную мощь, и потом скачаться в форме весов на рабочую сеть.
Распознавание
Перейдем теперь к экспериментальной оценке TDNN производительности распознавания. В частности, мы хотели бы сравнить производительность TDNN с производительностью в настоящее время наиболее популярного метода распознавания: скрытых Марковских моделей (СММ). Для сравнительной оценки, приведенной здесь, мы выбрали лучшие из числа HMM, развивавшиеся в нашей лаборатории. Несколько других основанных на HMM вариаций и моделей были опробованы в целях оптимизации нашей HMM, но мы не утверждаем, что исчерпывающие оценки всех основанных на HMM методов были получены. Мы также должны отметить, что эксперименты, приведенные здесь, были направлены на оценку двух разных методик распознавания. Каждый метод распознавания реализован и оптимизирован с помощью своих подходящих видов представления речевого сигнала, т. е. представления, которое хорошо подходит и наиболее часто используется для оцениваемого метода. Оценка обоих методов, конечно, осуществляется с использованием тех же входных данных речи, но мы предупреждаем читателей, что из-за различий в представлении, точный вклад в общую производительность распознавания способа представления сигнала неизвестен. Можно предположить, что оптимизация входного сигнала перед обработкой может повысить производительность для любой техники. В следующих разделах, мы начинаем с представления лучших наших скрытых Марковских моделей. Затем мы опишем экспериментальные условия и базу данных, используемую для оценки эффективности и заключения с достигнутыми результатами нашей TDNN и HMM.
База данных
Для оценки эффективности мы использовали обширную словарную базу данных, включающую 5240 японских слов. Эти слова были произнесены изолированно тремя мужчинами-японцами (МАУ, MHT, и MNM, все профессиональные дикторы) в порядке их появления в японском словаре. Все высказывания были записаны в звуконепроницаемой кабине приведены к частоте дискретизации. База данных была затем разделена на обучающее множество (четные файлы по порядку записи) и тестовое множество (нечетные файлы). Подготовленная база произношений и тестирования данных, таким образом, состояла из 2620 высказываний каждого, из нее были извлечены важные фонетические особенности.
Задачей распознавания, выбранной для этого эксперимента, было распознавание звонкие согласных, т. е. фонем "B", "D", и "G". Контрольные произношения были извлечены из высказываний, выбранных вручную акустическо-фонетических признаков, предоставленных базой данных. Обе методики распознавания, TDNN и HMM, были подготовлены и испытаны дикторозависимо. В обоих случаях, отдельные сети были подготовлены для каждого диктора.
В нашей базе данных не производился отбор лексем. Были отмечены все произношения, в которых были включены какие-либо из трех звонких согласных. Важно отметить, что так как согласные звуки были извлечены из всего высказывания, а не рассматривались в изоляции, существует значительное количество фонетических вариаций. Прежде всего, существует различный фонетический контекст, в зависимости от того, откуда извлечена фонема. Фактически сигнал "БА" будет значительно отличаться от "БИ " и так далее. Во-вторых, положение фонемы в высказывании приводит к дополнительным вариациям. В японском, например, "G" является назализованным, когда оно в середине высказывания, а не в начале. Оба наших алгоритма распознавания выдают только тип фонемы и должны найти свои собственные способы представления погрешностей речи. В таблице приведены результаты экспериментов распознавания, описанных выше, полученных на тестовом множестве. Как видно, для всех трех дикторов, TDNN дает значительно более высокую производительность, чем наши HMM. Усредненный по всем трем дикторам, уровень ошибки снижается с 6,3 до 1,5 процента, ошибка сокращается более чем в четыре раза.
Это особенно важно здесь для основной оценки производительности на данных тестирования, несколько наблюдений можно сделать, когда распознавание проходит обучающее множество. Для набора обучающих данных, процент правильно распознанных фонем: 99,6 процента (МАУ), 99,7 процента (MHT), и 99,7 процента (МНМ) для TDNN, и 96,9 процента (МАУ), 99,1 процента (MHT), и 95,7 процента (МНМ) для HMM. Сравнение этих результатов с теми же на тестовых данных показывает, что оба метода достигли хорошего обобщения из обучающего множества для неизвестных данных. Данные также показывают, что лучшая классификация, а не лучшее обобщение может быть причиной повышения производительности TDNN, показанной в таблице.