Реферат за темою випускної роботи
У роботі розробляється новий ефективний метод симуляції динаміки твердих, пружних тіл і рідин, що представленні у вигляді воксельних моделей.
Зміст
- Вступ
- 1. Актуальність теми
- 2. Мета і задачі дослідження та заплановані результати
- 3. Огляд досліджень та розробок
- 3.1 Огляд міжнародних джерел
- 3.2 Огляд локальних джерел
- 4. Опис запропонованого методу анімації воксельних моделей
- Висновки
- Перелік посилань
Вступ
Комп'ютери стали незамінним інструментом моделювання та симуляції. Зі збільшенням обчислювальної потужності, користувачі та програми вимагають все більші рівні реалізму в цих областях. Найбільш явно ця тенденція проявляється в комп'ютерній графіці, де моделюються все більш складні геометричні об'єкти і різноманітні фізичні процеси. Можливість моделювати і маніпулювати об'єктами, що деформуються, має важливе значення в контексті багатьох прикладних задачах. Існуючі підходи моделювання деформації об'єктів дозволяють використовувати як геометричні методи, в яких окремі точки, групи контрольних точок або параметри об'єкта змінюються відповідно до заданої форми, так і методи, що використовують фізичні закони, враховують властивості матерії, вплив зовнішніх сил та обмеження навколишнього середовища при моделюванні деформації об'єкта[4].
Існує безліч способів представлення тривимірних (3D) об'єктів, такі як полігональні моделі, воксели, CSG (конструктивна стереометрія), і т.д. Полігональні моделі — найбільш поширений формат серед інших завдяки їх використанню в комп'ютерній графіці і відеоіграх, а також підтримці цього представлення апаратними засобами графічних процесорів GPU. У вокселей є багато переваг у порівнянні з полігональнимі моделями. Основною перевагою є необмежений рівень деталізації. Основним недоліком вокселів, що заважає широкому застосуванню, є їх статичність. Анімація воксельних моделей є досить трудомістким і складним процесом.
Воксели — це кубоіди. Ідея полягає в тому, щоб апроксимувати 3D моделі безліччю (мільйонами) невеликих кубоідов, як це представлено на рисунку 1. Якщо деталізація воксельної моделі досить велика, воксели стають меншими ніж пікселі дисплея і не помітними на кінцевому зображенні. Модель сприймається як згладжена, без видимих виступів. Методи покращення зображення, згладжування, антіалайзінг повністю приховують базову структуру кубоіда воксельної моделі[1].

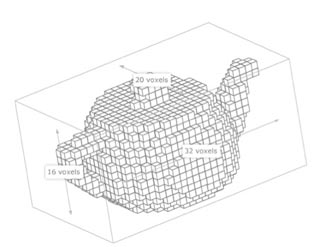
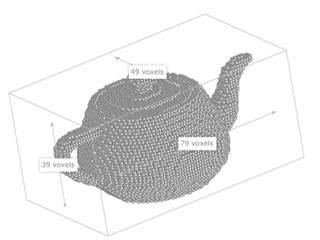
Рисунок 1 — Полігональна модель і воксельні моделі з низькою і високою деталізацією
Дослідження в області анімації, що використовує реальні фізичні властивості і закони, спрямоване на знаходження нових методів для моделювання фізичних явищ, таких як динаміка твердих тіл, пружних об'єктів або потоку рідини. Традиційний підхід до моделювання динамічних об'єктів використовує сили. На початку кожного кроку перераховуються внутрішні і зовнішні сили. Приклади внутрішніх сил — пружні сили або сили в'язкості і тиску в рідинах. Сила тяжіння — приклад зовнішньої сили. Другий закон руху Ньютона зв'язує сили з прискоренням тіла і його масою. Використовуючи усереднені маси вершин, сили перетворюються в прискорення. Будь-яка схема інтегрування часу може бути використана, щоб спочатку обчислити швидкості на основі прискорень, а потім позиції на основі швидкостей. Деякі підходи для управління анімацією використовують імпульси замість сил. Оскільки імпульси безпосередньо змінюють швидкості, один рівень розрахунків може бути пропущений [6].
Методи моделювання повинні задовольняти чотирьом головним вимогам, щоб бути застосовними в комп'ютерних іграх. Вони повинні бути швидкими, стійкими, керованими і простими у реалізації, для того щоб розробники ігор змогли використати їх у своїх проектах [7]. У комп'ютерних іграх, де стійкість і швидкість найчастіше більш важливі, ніж точність, більш прості і стійкі геометричні методи, такі як динаміка на основі позицій (Position Based Dynamics (PBD))[6], достатні, щоб створити необхідні фізичні ефекти.
1. Актуальність теми
Віртуальні середовища, в яких користувач може взаємодіяти з віртуальним світом, стали дуже популярними в останні роки. Тривимірні комп'ютерні ігри — важливий приклад. Вони представляють найбільший ринок у цій сфері. Крім комп'ютерних ігор, є велика кількість інших прикладів інтерактивних віртуальних середовищ, такі як засобу моделювання польоту, медичні та авто симулятори [3].
Щоб надати користувачеві відчуття реального фізичного світу, важливо, щоб об'єкти вели себе так, як вони ведуть себе в реальному світі. Віртуальні сцени, які зустрічаються в комп'ютерних іграх, включають в себе велику кількість об'єктів. Щоб змоделювати фізичні об'єкти — особливо, коли ці об'єкти деформовані або зруйновані на частини — можуть ефективно використовуватися воксели.
У зв'язку зі збільшенням потужностей комп'ютера і розвитком скануючих технологій воксельне представлення даних стало перспективним напрямком для проведення досліджень. В даний час широко використовуються тривимірні скануючі пристрої, і точки є привабливим примітивом для представлення складної високодеталізованих геометрії. Існує відносно мало розробок і літературних джерел, які пропонують ефективні методи анімації та моделювання динаміки воксельних моеделей.
Метою даної роботи є розробка ефективних алгоритмів анімації воксельних моделей. В роботі досліджується загальний підхід для створення анімації і моделювання динаміки об'єктів, що представленні вокселямі.
2. Мета і задачі дослідження та заплановані результати
Метою дослідження є розробка загального підходу анімації і моделювання динаміки твердих, пружних тіл і рідини, що представленні у вигляді вокселів.
Основні задачі дослідження:
- Огляд і аналіз існуючих методів анімації тривимірних полігональних моделей.
- Огляд і аналіз існуючих методів анімації воксельних моделей.
- Розробка нового ефективного методу анімації воксельних моделей.
- Програмна реалізація запропонованого підходу, розробка програмного забезпечення для створення анімованих сцен і їх відтворення.
- Аналіз отриманих результатів та оцінка ефективності розробленого алгоритму.
Об'єкт дослідження: анімація воксельних моделей.
Предмет дослідження: розробка методів і алгоритмів анімації і інтерактивної взаємодії об'єктів, що представленні воксельними моделями.
Результат дослідження: новий підхід анімації та моделювання інтерактивної взаємодії воксельних моделей; програмне забезпечення, що реалізує запропоновану методику.
3. Огляд досліджень та розробок
В останні роки анімація на основі фізики для інтерактивних систем була активним напрямком дослідження в комп'ютерній графіці, що призвело до появи нових методів і підходів у цій сфері. Серед фізичних процесів, які були змодельовані в режимі реального часу: динаміка твердого тіла, пружні об'єкти, рідини. Але більшість з цих методів підтримують роботу тільки з полігональними моделями, і не пристосовані для роботи з вокселями.
3.1 Огляд міжнародних джерел
Починаючи з ранніх робіт, безліч методів було запропоновано для моделювання пружних, твердих тіл, тканин і рідини. Перші методи моделювання використовувалися тільки в оффлайнових обчисленнях. Обчислювальна потужність, наявна сьогодні, дозволяє моделювання цих ефектів в реальному часі.
У статті [ 1 ] Denis Bautembach представляє загальний спосіб анімації розрідженного октодерева під час процесу рендеринга.
В роботі [ 2 ] Ciryl Crassin розглядає метод візуалізації великих наборів даних використовуючи воксели. Він використовує інформацію, отриману під час процесу рендеринга, щоб регулювати процес потокової передачі. Їх технологія, Gigavoxels
не обмежена стереометрії і може моделювати атмосферні ефекти, такі як хмари.
Branislav Siles створив графічний движок Atomontage
[ 20 ], що дозволяє візуалізувати високо деталізовані, візуально привабливі сцени. Важливою рисою, що виділяє цю технологію серед інших, є можливість працювати одночасно з воксельних моделями і з полігональними. Мета Atomontage полягає в тому, щоб використовувати воксели не тільки для візуалізації, але також і для моделювання фізики, хімії та деяких інших заснованих на атомі наукових моделей.
Технологія Unlimited Detail
[ 21 ] розробляється австралійською компанією Euclideon з 2004 року. Основними розробниками є Bruce Dell і Greg Douglas. Unlimited Detail
— програмна технологія в тривимірній комп'ютерній графіці, призначена для зберігання і рендеринга віртуальної тривимірної сцени за допомогою хмари точок в режимі реального часу.
Основні технологічні аспекти «Unlimited Detail» публічно не відомі, проте розробники заявляють, що їхня технологія дозволяє відображати на сцені необмежену кількість об'єктів з дуже високою деталізацією без істотної втрати продуктивності.
В роботах [ 6 ] та [ 7 ] представлен універсальний підхід анімації об'єктів Position Based Dynamics (PBD), що дозволяє моделювати складні фізичні моделі і процеси.
3.2 Огляд локальних джерел
В результаті пошуку робіт, присвячених тематиці даної роботи, не було знайдено жодної роботи відповідно даному напрямку. Поверхневий огляд воксельної графіки було дано у роботах магістрів С.С. Захарова Моделювання земної поверхні
[ 17 ], Н.О. Харченка Структурно-алгоритмічна організація пристроїв генерації довільних дуг і секторів в 3D просторі для об'ємних дисплеїв
[ 18 ] і В.Н. Кудрі Дослідження і розробка алгоритмів синтезу моделей геометричних об'єктів
[ 19 ]. Тим не менш, зміст цих робіт має іншу спрямованість.
4. Опис запропонованого методу анімації воксельних моделей
В останні роки воксельна графіка набула важливе значення, так як потужності сучасних комп'ютерів дозволяють зберігати й обробляти високодеталізовані воксельні моделі у реальному часі. У своїй перспективі, даний вид представлення даних має потенціал зайняти важливе місце серед технологій комп'ютерного моделювання і візуалізації. Вже сьогодні воксельні моделі використовуються у безлічі додатків, включаючи медичну обробку зображень, гідроаеродинаміки, моделювання ландшафту, генерація тектури, і останнім часом навіть в комп'ютерних іграх [ 9 ].
Ймовірно, найпростіший формат зберігання воксельної моделі — регулярна координатна сітка. Модель може бути представлена як тривимірний масив у якому кожна клітинка описує один воксель. Це подання є неефективним з точки зору пам'яті.Більш ефективне рішення, яке використовується в більшості випадків — розріджене воксельне октодерево (Sparse Voxel Octree (SVO)). SVO — це деревовидна структура даних, в якій у кожного вузла може бути до восьми дочірніх елементів. Дерево розріджено в тому сенсі, що воно не включає піддерева, що відповідають порожньому вокселю. Основна ідея полягає в тому, щоб починаючи з одного великого кубоіда і рівномірно розділяючи його на вісім менших кубоідов, повторювати рекурсивно цей процес для кожного дочірнього елемента поки необхідна деталізація не буде досягнута. Рисунок 2 ілюструє це поняття.
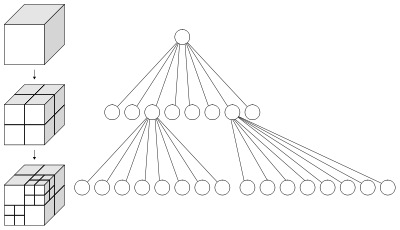
Рисунок 2 — Сруктура розрідженого октодерева
SVO дуже ефективно використовує пам'ять (сучасні графічні движки можуть стиснути обсяг пам'яті, що спожівається одним вокселем, до одного біта), а їх ієрархічна структура вигідна багатьом операціям, що вікорітсовуються в комп'ютерній графіці. Воксели підходять для того, щоб представляти моделі з високодеталізованою мезоструктурою, такі як скелі, гори, ландшафт, рослинність, природа[1].
Воксели не підходять для представлення плоских поверхонь, що використовуються, наприклад, в архітектурі і дизайні меблів. Такі поверхні можуть бути змодельовані невеликим числом полігонів, тоді як у воксельних моделей завжди повинно бути максимальна деталізація, щоб здаватися гладкими незалежно від того яку поверхню вони представляють [1].
Тому не можна дотримуватися тільки однієї технології, тільки їх спільне застосування дозволить досягти найкращих результатів.
У комп'ютерній графіці і особливо в комп'ютерних іграх найчастіше бажано мати пряме управління положеннями об'єктів або вершинами полігональної сітки. Користувач може прив'язати вершину до кінематичному об'єкту або упевнитися, що вершина завжди залишається поза певній галузі. Метод динаміки на основі позицій (Position Based Dynamics (PBD)) працює безпосередньо з позиціями, що робить такі маніпуляції легко реалізованими.
В початковому підході PBD модельований об'єкт представляється набором із N контрольних точок і M обмежень. Кожна контрольна точка i має атрибути приведені в таблиці 1.

Обмеження j визначається п'ятьма атрибутами наведеними в таблиці 2. Обмеження з типом рівність
задовольняється якщо C j (x i1 , ..., x inj ) = 0. Якщо тип нерівність
, то обмеження задовольняється якщо C j (x i1 , ..., x inj ) ≥ 0. Параметр жорсткості k j визначає силу впливу обмеження і може приймати значення від 0 до 1.

Таким чином, головні особливості та переваги динаміки заснованої на позиціях:
- моделювання дає контроль над процесом зміни позицій і не схильне до типових проблем нестійкості;
- положеннями вершин і частинами об'єктів можна безпосередньо керувати під час моделювання;
- дозволяє обробляти загальні обмеження при перерахуванні позицій;
- метод легко зрозуміти і реалізувати.
Результат моделювання взаємодії двох об'єктів наведено на рисунку 3 (зліва показані контролні точки та звязки, зправа – кінцевий результат). У цьому прикладі, м'яч являє собою тверде тіло, сітка — систему, що деформується (контрольні точки виділені червоним кольором). Всі обчислення при моделюванні виконані з використанням динаміки заснованої на позиціях (PBD).


Рисунок 3 – Приклад моделювання зіткнення твердого тіла і динамічної системи
(анимація: 18 кадрів, 10 циклів повторення, 140 KB)
Основну ідею запропонованого підходу анімації воксельного октодерева можна викласти в наступних твердженнях
- Кожен вузел SVO дерева обробляється як окрема частинка, може бути модифікований / трансформований незалежно від батьківських вузлів.
- Кожен вузел SVO дерева або має свій набір властивостей і обмежень, або успадковує їх від батьківського вузла.
- На кожному кроці вузли SVO дерева трансформуються певним чином.
- На кожному кроці, використовується динаміка на основі позицій (PBD) для перерахунку і коректування позицій і швидкостей.
Висновки
У роботі розробляється новий ефективний метод анімації воксельних моделей. На даний момент існує велика кількість методів анімації тривимірних полігональних моделей, але напрямок анімації моделей, які мають воксельне представлення, ще не достатньо розкрит. Це питання стає все більш актуальним особливо у світлі того, що за останні роки зріс інтерес до воксельної графіку.
Магістерська робота присвячена актуальній науковій задачі пошуку нових методів і підходів для анімації тривимірних воксельних моделей. На підставі аналізу літературних джерел виділено основні алгоритми і структури представлення даних, які можуть бути використані і розширені в запропонованому підході анімації і сіммуляціі взаємодії інтерактивних воксельних моделей.
Подальші дослідження спрямовані на наступні аспекти:
- Розширити і адаптувати розглянуті методи і підходи для ефективної роботи з об'єктами, представленими воксельними моделями.
- Якісне вдосконалення запропонованого підходу анімації.
- Програмна реалізація розроблених методів та алгоритмів.
- Сіммуляція твердих, пружних тіл і рідин.
- Аналіз експерементальних результатів та ефективності розробленого підходу.
- Розробка кроссплатформенного програмного забезпечення для створення аніміруемих сцен і їх відтворення.
При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення: грудень 2012 року. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після вказаної дати.
Перелік посилань
- Bautembach D., Animated Sparse Voxel Octrees // Bachelor’s Thesis – University of Hamburg, Department of Informatics, 2011, http://www.bautembach.de ...
- Crassin C., GigaVoxels: A Voxel-Based Rendering Pipeline For Efficient Exploration Of Large And Detailed Scenes // PhD thesis – Universite de Grenoble, 2011 http://www.maverick.inria.fr ...
- Muller M., Teschner M., Gross M., Physically-Based Simulation of Objects Represented by Surface Meshes // Proceedings of Computer Graphics International (CGI), Crete, Greece, Jun 16-19 2004, pp 26-33, http://www.matthiasmueller.info ...
- Gibson S., Mirtich B., A Survey of Deformable Modeling in Computer Graphics // Mitsubishi electric research laboratories, Technical Report TR-97-19, MERL, 1997 http://www.merl.com ...
- Nealen A., Muller M., Keiser R., Boxerman E., Carlson M., Physically Based Deformable Models in Computer Graphics // Computer Graphics Forum, 2006, Volume 25, pp 809–836, http://citeseerx.ist.psu.edu ...
- Muller M., Heidelberger B., Hennix M., Ratcliff J., Position Based Dynamics // Proceedings of Virtual Reality Interactions and Physical Simulations (VRIPhys), – Madrid, 2006, – pp 71-80, http://www.matthiasmueller.info ...
- Muller M., Hierarchical Position Based Dynamics // Proceedings of Virtual Reality Interactions and Physical Simulations (VRIPhys2008), Grenoble, 2008 http://www.matthiasmueller.info ...
- Muller M., Chentanez N., Solid Simulation with Oriented Particles // ACM Transactions on Graphics (SIGGRAPH 2011), 2011, pp 92:1-92:10, http://www.matthiasmueller.info ...
- Karabassi A., Papaioannou G., Theoharis T., A Depth Buffer Based Voxelization Algorithm // Department of Informatics, University of Athens, 2000 http://www.cgi.di.uoa.gr ...
- Figueiredo M., Oliveira J., Araujo B., Pereira J., An efficient collision detection algorithm for point cloud models // Міжнародна конференція з комп'ютерної графіки GraphiCon, 2010, http://www.graphicon.ru ...
- Limtrakul S., Hantanong W., Kanongchaiyos P., Nishita T., Reviews on physically based controllable fluid animation // Engineering Journal, Vol 14, 2010, http://www.engj.org ...
- Belyaev S., Laevsky I., Chukanov V., Real-time Animation, Collision and Rendering of Grassland // Міжнародна конференція з комп'ютерної графіки GraphiCon, 2011, http://www.graphicon.ru ...
- Катасонов А.В., Вяткин С.И., Долговесов Б.С., Вокселизация функциональных форм // Міжнародна конференція з комп'ютерної графіки GraphiCon, 2005, http://www.graphicon.ru ...
- Семакин М.М., Метод синтеза движений в задачах трехмерной компьютерной анимации // Bachelor’s Thesis – University of Hamburg, Department of Informatics, 2011, http://www.graphicon2002 ...
- Бобков В.А., Мельман С.В., Роньшин Ю.И., Оптимизация трассировки лучей в октантных деревьях // Міжнародна конференція з комп'ютерної графіки GraphiCon, 2005, http://www.graphicon.ru ...
- Лисицин Е., Конушин А., Подгонка параметрических моделей к облакам трехмерных точек // Міжнародна конференція з комп'ютерної графіки GraphiCon, 2006, http://www.graphicon.ru ...
- Захаров С.С., Моделирование земной поверхности // Магістерська робота, керівник: д.т.н., профессор Башков Е.А., 2005, http://masters.donntu.ru ...
- Харченко Н.О., Структурно-алгоритмическая организация устройств генерации произвольных дуг и секторов в 3D пространстве для объёмных дисплеев.// Магістерська робота, керівник: д.т.н., профессор Башков Е.А., 2011, http://masters.donntu.ru ...
- Кудря В.Н., Исследование и разработка алгоритмов синтеза моделей геометрических // Магістерська робота, керівник: к.т.н., доц. Карабчевский В.В., 2003, http://masters.donntu.ru ...
- Офіційний сайт проекту Аtomontage Engine // Режим доступа http://www.atomontage.com
- Офіційний сайт проекту Unlimited Detail // Режим доступа http://www.euclideon.com/
