Abstract
Content
- Introduction
- 1. The general formulation of the problem
- 2. Formulation of the problem
- Conclusion
- References
Introduction
The preparatory stage of cutting production is classified as intellectually-intensive production processes. For this reason, the economic performance of enterprises in which the cutting operations are performed directly are associated with the task of automating the optimal flow of materials [1].
In practice, the process of optimizing the consumption of rolled materials depends on the optimality cut maps drawn up by the enterprises. In addition, it should be noted that this process requires processing large amounts of information (information about the passport material requirements for the optimality of organizational features of a particular enterprise, etc.) - all of those parameters that are used when you are calculating-filled [5].
At present, the solution of this problem is based on experience and intuition of skilled workers in this field. Performing such work without the involvement of computational tools, naturally doesn’t lead to inefficient expenditure of time, human and material resources. So, that’s why requires the development of modern computational tools (programs), allowing to form solutions with a greater degree of optimality, and scientific validity. This is particularly relevant in an increasingly competitive market. Details d should be optimally placed on the material surface D with the following conditions:
1. The general formulation of the problem
In today's small-scale production of parts engaged in manufacturing sheet (roll) of the material, rather acute problem of optimal cutting of the material as well as the correct cut in the first place, will reduce the material costs of resources and thus reduce the dependence of production costs of finished products, to improve its competitive condition, and ultimately more profit. Thus, among the existing reveal the following: curly, oblique, rectangular [1]. Figured nesting places on the map detail not rectangular, oblique has rectangular shape, but are not positioned parallel to the edges of the material. The rectangular cutting works only with the details of a rectangular shape, which are nesting on the map with the following restrictions [8] :
1. edges are parallel to the edges of objects bands
2. objects do not intersect with each other
3. objects do not intersect with the parties to the band
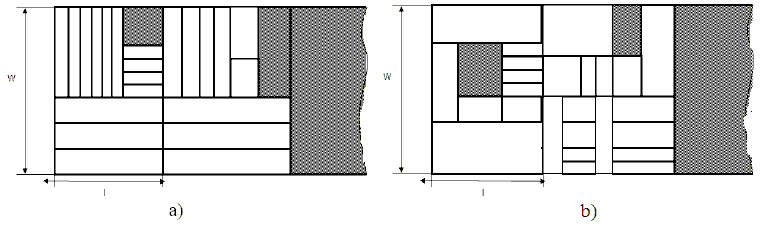
Also, the rectangular cutting may be guillotine (see fig. 1. a) and not guillotine (fig. 1 b). Under the guillotine cutting is understood, implemented by a sequence of cross-cuts parallel to the edges of the material (fig. 1 a). In fig. 1 b is represented not guillotine cutting. Cutting, which will be discussed in this article will be rectangular, not guillotine and roll (stripe size: width = const, length = ∞) [6].
2. Formulation of the problem
The problem that must be solved in this paper can be summarized as follows. We have a starting material D = {W, L} is the raw material, semi-infinite rectangular, its width is a fixed size W = const, and its length is relatively infinite L ≈ ∞, , also we have vectors of the rectangular components of a certain size d = {d 1(w 1, l 1) , d 2(w 2, l 2), … , d i(w i, l i), … , d k-1(w k-1, l k-1), d k(w k, l k)} and their counts n = {n 1, n 2, … , n i, … ,n k-1, n k}. Details d should be optimally placed on the material surface D with the following conditions [1, 2]:
• wi are parallel or perpendicular to (if you intend to turn parts up to 90 °) W - a condition squareness of cuts [1];
• d i∩ d j = {l;∅ }, where l – segment - the details do not intersect with each other;
• d i∩ D = d i – details are beyond the source material.
It is assumed that the using of multiple criteria optimal placement of components having different priorities [8]. That is, when the first priority of the optimum placement for optimum shown in the following priority, etc.
To describe this problem optima in accordance with their priorities:
1. Optimum would be such a sequence P i placement of parts, in which L '(P i) > min, where L' - length of the start raw material L.
2. From the selected of the first priority will be those best sequence K i, where the K (P i) > min, where K '- the number of necessary cuts.
3. From the selected of second priority will be those best sequence Oi, where the O (K i) > min, where the O - the area of the wastes.
It should be noted that the problem is the same additional conditions of production optimization, which may include:
• possibility of increasing the size of parts within the prescribed limits in order to minimize waste and cuts [10];
• limit the number of parts in podkorzine (one or more);
• the possibility of turning parts up to 90 °.
• consideration of the edge magnitude as for the details, and for the material.
Conclusions
Currently, all the more relevant are issues of automation in full to a possible transition to the creation of an enterprise integrated information environment that enables flexible integration of modern design, production, management, etc., which can effectively solve the problem of operational planning of production. Therefore, in such circumstances is particularly important to search for n ew approaches to restructuring the system provides an efficient calculation of the optimal cut cards with a view of the realities of life. The level of development of computer technology allows you to fully solve successfully the tasks required to practice in the volume and quality. One such example is presented in this paper.
While writing the given abstract the master's work has not been completed yet. The final date of the work completed is December, 2012. The text of master's work and materials on this topic can be received from the author or her research guide after the indicated date.
References
1. Мухачева A.C., Ширгазин P.P. Задачи упаковки прямоугольников: рандомизиро-ванная эвристика на базе двойственной схемы локального поиска оптимума // Информационные технологии. 2003. №5. С. 18-23.
2. Мухачева A.C., Чиглинцев A.B. Генетический алгоритм поиска минимума в задачах двумерного гильотинного раскроя // Информационные технологии. 2001 №3. С. 27-32.
3. Норенков И.П. Эвристики и их комбинации в генетических методах дискретной оптимизации. // Информационные технологии. 1999. №1. С. 2-7.
4. Валиахметова Ю.И., Карамова Е.В. Расширение генетического алгоритма комбинирование эвристик для решения задачи прямоугольной упаковки // Вестник ВЄГУ № 2, 2009. С. 40. [Электронный ресурс] – http://www.work.vegu.ru/vegu...
5. Балабанов В.Н. Многокритериальная задача рационального ппланирования продольного раскроя рулонного материала //Проблемы информационных технологий. – 2009. – №2 С. 206. [Электронный ресурс] – http://www.nbuv.gov.ua/portal
6. Петров Ю. Ю. Регуляция вероятностей кроссинговера и мутации /Инфотелекоммуникационные технологии в науке, производстве и образовании // Первая международная научно-техническая конференция. Ставрополь: СевКавГТУ, 2004.
7. Применение распределённого генетического алгоритма при решении задачи об упаковке в
контейнеры / Ю. А. Бюргер, В. Й. Гнатюк, В. И. Литвиненко, А. А. Ткачук // Перспективные
информационные технологии и интеллектуальные системы, 2003.
8. Данилина И.И. Алгоритмы перебора. [Электронный ресурс] – http://inf.1september.ru/2000...
9. Мастяева И.Н., Семенихина О.Н. Методы оптимизации. [Электронный ресурс] – http://www.google.com.ua/...
10. Скурихин А.Н. Генетические алгоритмы // Новости искусственного интеллекта № 4. – Москва 1995. – С. 6–46.
