Автоматизированная система составления оптимальных схем раскроя рулонного материала

 Аннотация

Семиндеева Е.Г. Фонотов А.М. Автоматизированная система составления оптимальных схем гильотинного раскроя рулонного материала. Рассматривается задача гильотинного раскроя рулонного материала. Данная задача сводится к упаковке прямоугольников в полубесконечную полосу заданной ширины, где требуется минимизировать длину занятой части полосы с учетом ограничений и дополнительных условий. Произведена формализация данной задачи, а так же предложены методы и алгоритмы ее решения.

  Введение

  Подготовительно-раскройный этап производства относится к классу интелектуальноемких процессов производства. Именно поэтому, во многом экономические показатели предприятий, на которых выполняются операции раскроя, напрямую связаны с задачей автоматизации оптимального расхода материалов.

  На практике, процесс оптимизации расхода рулонных материалов зависит от оптимальности карт кроя, составляемых на предприятиях. Кроме того, следует отметить, что данный процесс требует обработки значительных объемов информации (информации о паспортах материалов, требований по оптимальности, организационных особенностей конкретного предприятия и т.п.) – всех тех параметров, которые используются при выполнении расчета. В настоящее же время решение данной задачи основывается на опыте и интуиции квалифицированных работников данной сферы. Выполнение подобной работы без привлечения вычислительных средств, естественно приводит к не эффективным затратам временных, людских и материальных ресурсов. Поэтому требуется разработка современных вычислительных средств (программ), позволяющих формировать решения с большей степенью оптимальности и научной обоснованностью. Это особенно актуально в условиях все возрастающей конкуренции на рынке.

  Общая постановка проблемы

  В условиях современного мелкосерийного производства занимающегося изготовлением деталей из листового (рулонного) материала, достаточно остро стоит вопрос об оптимальном раскрое данного материала, так как правильный раскрой, в первую очередь, позволит сократить материальные затраты ресурсов и соответственно снизить себестоимость готовой продукции, повысить ее конкурентные кондиции и в конечном итоге получить большую прибыль. Итак, среди существующих раскроев можно выделить следующие: фигурный, косоугольный, прямоугольный. Фигурный раскрой размещает на карте детали непрямоугольной формы, косоугольный – прямоугольной формы, но расположенным не параллельно граням материала. Прямоугольный раскрой работает только с деталями прямоугольной формы, которые на карте раскроя располагаются со следующими ограничениями:

  •  ребра предметов параллельны ребрам полосы;
  •  предметы не пересекаются друг с другом;
  •  предметы не пересекаются со сторонами полосы;

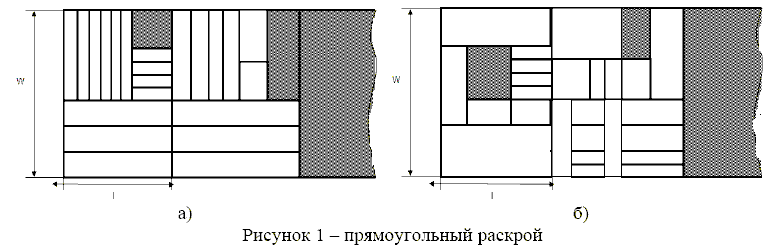
  Также прямоугольный раскрой может быть гильотинный (рис. 1. а) и негильотинный (рис. 1 б). Под гильотинным понимается раскрой, реализуемый последовательностью сквозных резов, параллельных кромкам материала (рис. 1 а). На рис. 1 б представлен негильотинный раскрой. Раскрой, о котором пойдет речь в данной статье будет прямоугольным, гильотинным и рулонным (размер полосы: ширина = const, длина = ∞ ).

  Постановка задачи

  Поставленную задачу, которую необходимо решить в данной работе можно сформулировать следующим образом: имеется исходный материал D = {W, L} полубесконечной прямоугольной формы, т.е. ширина имеет фиксированный размер W = const, а длина является условно бесконечной L ≈ ∞, а также векторы типоразмерностей прямоугольных деталей d = {d ₁(w ₁, l ₁) , d ₂(w ₂, l ₂), … , d _i(w _i, l _i), … , d _k-1(w _k-1, l _k-1), d _k(w _k, l _k)} и их количество n = {n ₁, n ₂, … , n _i, … ,n _k-1, n _k}. Необходимо оптимально разместить детали d на поверхности материала D с соблюдением следующих условий:

  wi параллельно или перпендикулярно (если предполагается поворот детали на 90°) W – условие прямоугольности резов;

  • d _i∩ d _j = {l;∅ }, где l – отрезок – детали не пересекаются друг с другом;
  • d _i∩ D = d _i – детали не выходят за пределы исходного материала;

  Предполагается использование нескольких критериев оценки оптимальности размещения деталей, имеющих различный приоритет. То есть, при выполнении оптимума первого приоритета отбирается размещение по оптимуму следующего приоритета и.т.д. Для данной постановки опишем оптимумы в соответствии с их приоритетами:

  1. Оптимальными будут такие последовательности P _i размещения деталей, при которых L'(P _i) > min, где L' – длина использованного исходного материала L.

  2. Из отобранных по первому приоритету оптимальными будут такие последовательности K _i, при которых K(P _i) > min, где K' – количество необходимых резов.

 3. Из отобранных по второму приоритету оптимальными будут такие последовательности O _i, при которых O(K _i) > min, где O – площадь полученных отходов.

 Следует отметить, что в постановку задачи входит так же дополнительные условия производственной оптимизации, которые могут включать:

  • возможность увеличения типоразмера деталей в заданных пределах для минимизации количества отходов и резов;
  • ограничение на количество деталей в подкорзине (одна или несколько);
  • возможность поворотов деталей на 90°;
  • учет величины кромки, как для деталей, так и для материала.

  Возможные методы решения

  Задачи подобного рода относятся к категории NP-сложных в том смысле, что не возможно ее решение полиномиальное от количества элементов время. Классическими образцами в более простых постановках таких задач являются задачи о коммивояжере и упаковке рюкзака. Такие задачи не могут быть решены с использованием только эвристических алгоритмов.

Результат решение поставленной в данной работе задачи может быть точным или оптимальным.

  Точное решение поставленной задачи можно получить только методом полного перебора перестановок деталей на поверхности исходного материала всех возможных последовательностей размещения. Этот метод имеет смысл применить при небольшом количестве деталей. Но когда речь идет о реальных масштабах производства, применить этот метод становиться проблематичным, так как для такого решения необходимо обработать данные, размер которых равен факториалу от количества деталей, что является в принципе невозможным из-за ограниченности вычислительных ресурсов ЭВМ. Так, например, имея N деталей, мы получаем N! перестановок, а если детали могут быть ориентированы двумя способами, число перестановок будет равна (2N)!, т. е. применяется каждая из них с поворотом на 90 ° предметами.

  Следует отметить, что для оптимизации нахождения оптимумов размещения можно применить известные методы такие как муравьиные алгоритмы, генетические алгоритмы. Очевидно, что методы использующие алгоритмы нейронных сетей нам не подходят, так как они ориентированы на обучение с «учителем», а количество обучающих наборов в этом случае будет бесконечно велико.

  На мой взгляд, наиболее подходящим методом для решения поставленной задачи будет определенным образом модифицированный генетический алгоритм, который имеет свойство сходимости в экстремумах фитнес-функций. Так как поставленная задача является многоэкстремальной, можно говорить о том, что найденный экстремум не обязательно будет являться глобальным, поэтому полученный результат может отличаться от точного, но при увеличении времени обработки и предотвращении преждевременной сходимости можно получить оптимальное решение достаточное для решения бизнес-задачи производства.

  Идея эволюционного алгоритма «подсмотрена» у природы и основана на четырех взаимосвязанных естественных процессах обеспечивающих приспосабливаемость популяции к воздействию среды, а именно селекция, скрещивание, мутация и отбор. Описание программных реализаций эволюционных алгоритмов реализующих эти этапы описаны достаточно подробно в литературе и выходит за рамки данной статьи.

  Хромосома, представляющая потенциальное решение может иметь соседское, порядковое или путевое представление (предварительно все детали нумеруются без учета типоразмера). Наиболее перспективной для данной задачи, по моему мнению, является путевое представление хромосомы как наиболее естественное и удобное для трансформации самого алгоритма. Пространственная интерпретация данного представления может быть организована по эвристике «лучшая корзина», которая предполагает размещение очередной детали по принципу максимального использования площади пространства (корзины) отсеченных прямыми резами вдоль ребер деталей, уложенных ранее.

  Для реализации решения, при котором допускается поворот детали можно ген представить в виде пары {i,j}, где i – порядковый номер детали, а j – аллель {0,1}, где 0 – без поворота, 1 – с поворотом. Однако при таком подходе, во-первых, резко возрастает генофонд, а во вторых варианты кроссинговера являются не столь очевидными.

  Вторым вариантом представления хромосомы является последовательная сцепка двух векторов: вектора порядков и вектора положений (далее будем называть такую хромосому последовательной). Например, 1-3-4-2-5 | 0-1-1-0-1 означает, что деталь № 1 укладывается без поворота, следующая за ней деталь № 3 – с поворотом и т.д.. При этом кроссинговер и мутация выполняется отдельно для каждого из векторов. Например, для первого вектора кроссинговер типа PMX (частично отображаемый), а для второго вектора – обычный бинарный одноточечный или двухточечный кроссинговер.

  Недостатком использования всей длины последовательной хромосомы является поле вариантов (генофонд) на котором ожидается сходимость популяции к минимальному экстремуму.

  Как вариант сокращения поля можно попытаться использовать «вложенный» генетический алгоритм. Идея заключается в следующем. Генетический алгоритм первого уровня отрабатывает вектор порядков, сокращая тем самым поле поиска решения, а вектор поворотов рассчитывается встроенным независимым генетическим алгоритмом и его результат «приклеивается» к основному вектору порядков. То есть выигрыш ожидается за счет разбиения основной задачи на две подзадачи: поиска оптимального порядка и поиска оптимальных поворотов деталей, каждая из которых решается на значительно меньшем поле за счет чего, ожидается повышение результативности алгоритма.

  Новым так же в постановке задачи является использование ступенчатой фитнес- функции, которая рассчитывается следующим образом:

  • если значения функции i-го приоритета для двух хромом различны, тогда хромосома с меньшим значением считается более приспособленной;
  • при равенстве значений функции i-го приоритета сравниваются значения функции i+1 приоритета.

  Выводы

  В настоящее время все более актуальными становятся вопросы автоматизации производства в полном объеме с целью возможного перехода к созданию на предприятии единой информационной среды, позволяющей гибкое интегрирование современных средств проектирования, производства, управления и т.д., которые позволяют эффективно решать задачи оперативного планирования производства. Поэтому в таких условиях особенно важным становится поиск новых подходов, обеспечивающий целесообразную перестройку системы оптимального расчета карт кроя с учетом жизненных реалий. Уровень развитие вычислительной техники позволяет вполне успешно решать поставленные задачи в необходимом для практики объеме и качестве. Один из таких примеров представлен в данной статье.

  Список использованной литературы

  1. Мухачева A.C., Ширгазин P.P. Задачи упаковки прямоугольников: рандомизированная эвристика на базе двойственной схемы локального поиска оптимума // Информационные технологии. 2003. №5. С. 18-23.
  2. Мухачева A.C., Чиглинцев A.B. Генетический алгоритм поиска минимума в задачах двумерного гильотинного раскроя // Информационные технологии. 2001 №3. С. 27-32.
  3. Норенков И.П. Эвристики и их комбинации в генетических методах дискретной оптимизации. // Информационные технологии. 1999. №1. С. 2-7.
  4. Ермаченко А.И., Сиразетдинов Т.М. Автоматизированная система расчета прямоугольного раскроя // Информационные системы и технологии. Новосибирск: НГТУ, 2003. С. 36-39.
  5. Сиразетдинов Т.М. Автоматизированная система расчета прямоугольного раскроя // Принятие решений в условиях неопределенности. Уфа: УГАТУ, 2003. С. 329-339.