Автор статьи: Wang Shoukun, Wang Jingchun, Jin Yihui
Автор перевода: Е.Г. Семиндеева
Источник: An improved genetic algorithm for rectangles cutting & packing problem
После рассмотрения общих вопросов и описания алгоритмов задачи резки и упаковки, в этой статье предложен улучшенный генетический алгоритм для не гильотинного прямоугольного раскроя. Во-первых, самоадаптивная вероятностная мутация будет предотвращать преждевременную сходимость алгоритма, также сравниваются некоторые часто используемые операторы кроссинговера, и стохастическое самовосхождение к оптимуму операторов ГА, направленных на улучшение локальных возможностей поиска экстремума. Во-вторых, жадный механизм вводится с целью получить хороший образец упаковки, представленный последовательным порядком упаковки определенного ГА. Результаты расчетов показывают эффективность этих улучшений. Copyright © 2002 IFAC
Ключевые слова: генетический алгоритм, случайный поиск, эвристический поиск, глобальная оптимизация, задачи упаковки
Задача упаковки была широко изучена в течение прошлых трех десятилетий, поскольку к ней часто прибегали в таких в отраслях, как металлообработка, ткацкое и бумажное производство. Задача упаковки прямоугольных элементов, вырезанных из материала прямоугольной формы является частным случаем комплекса задач упаковки. Целью данной задачи является минимизация отходов.
Задача упаковки относится к NP трудным задачам, это доказано уже во многих источниках. Поскольку геометрические характеристики упаковки объектов должны быть также приняты во внимание, а их вычислительные алгоритмы являются более сложными для разработки. На основе описания характеристик раскроя и его решения, Дикхов (1990) классифицировал задачи раскроя на пять категорий:
• Раскрои и отходы;
• Упаковка корзины, упаковка полосы, и рюкзака;
• Загрузка транспортного средства, загрузка поддона и загрузка контейнеров;
• Ассортимент элементов, набор материала, цель, размещение, схема размещения;
• Объем ресурсов и памяти, возможности многопроцессорных вычислений.
Как правило, проблемы резки материала можно разделить на обычную задачу упаковки и нестандарные упаковки проблемные по форме, а также в одномерном, двумерные, трехмерные и многомерных задач упаковки их диапазона из пространства решений.
Самая ранняя литература по проблемам резки материала появились в 1939 году, но на самом деле бум академических научно-исследовательских работ возник с 1970-х годов. Gyson и Gregory (1974) впервые выдвинули эвристический алгоритм упаковки. А затем традиционные алгоритмы оптимизации, такие как правило на основе алгоритма упаковки (Madsen, 1979), ветвление и ограничение (Golden, 1976), динамическое программирование (Golden, 1976), и интегральное программирование (Farley, 1988) были осуществлены по этому данному вопросу комплексно. Kofman и Shora (1990) выдвинули тест для оценки эффективности алгоритмов упаковки, который был описан как упаковка определенного количества клеток со случайными границами между 0 и 1 в единицу широкой длинной прямоугольный бесконечной полосы.
Современные технологии оптимизации сделали замечательный прогресс, достигнутый после 1990-х годов. Генетические алгоритмы, имитации отжига, нечеткий поиск, нейронные сети и другие метаэвристические алгоритмы поиска показали значительный прогресс, особенно в комбинаторных задач оптимизации. Jakobs (1996), который предложил алгоритм BL (bottom-left) - на основе генетического алгоритма для упаковки прямоугольников; Hopper и Turton (1999), Liu и Teng (1999) выдвинули свои улучшенные решения соответственно, Faina (1999) предложил применение алгоритма имитации отжига для задачи упаковки деталей. На основании четырех документов указанных выше в данной статье предложен модифицированный генетического алгоритм: задача прямоугольной упаковки с новым набором элементов, алгоритм оценки показателей. Чтобы показать свою эффективность включены результаты моделирования.
Эта статья организована следующим образом. В разделе 2 вводится понятия генетического алгоритма, модель задачи упаковки и показатель оценки качества. В разделе 3 обсуждается в деталях реализация не гильотинные алгоритмы раскроя. В разделе 4 моделирование численных результатов и на примерах показаны и объяснены преимущества этих алгоритмов. Наконец в заключении, предложенном в разделе 6, исследованы проблемы дальнейшего изучения данной задачи.
Генетические алгоритмы (ГА) представляет собой мощную стратегию нахождения глобальных оптимумов, основанную на моделировании генетики и эволюции в природе(Голландия, 1975). Его применение в резке и упаковке условно можно разделить на два метода. Один основан на координатах мелких предметов в двоичном или десятичном кодировании [12]. Другой основан на порядке размещения или резки в кодировании целыми числами [7, 8, 9]. Проведя тщательное моделирование и опыты с ГА - проектированием, было обнаружено, что первые вызовы метода высокого уровня разработки на элементах фитнес функции приспособленности, легко попадают в несуществующее решение или локальный оптимум; второй метод должен быть объединен с другим алгоритмом, чтобы генерировать образцы упаковки, что может так или иначе нивелировать недостатки первого метода. На основе второго метода нового алгоритма упаковки были разработаны генетические операторы, которые улучшили структуру и параметры управления ГА, и они также улучшают точность и устойчивость алгоритма.
Общая структура задачи резки и упаковки заключается в следующем:
1. Одна или более групп определенных фигур, форм и размеров;
2. Много мелких предметов, которые будут вырезаны или упакованы с различными параметрами, формами и размерами;
3. Учет и расчет некоторых ограничений;
4. Оценка критериев на основе одной или нескольких целей.
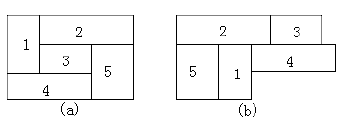
Одним из основных ограничений является ограничение на рез. В таких отраслях как стекло, бумажное производство требуется, чтобы рез был сквозным от края до края прямоугольного листа. Такой рез осуществляет гильотина. Если рез не скрозной, т.е. не пересекает весь раскраиваемых материал, то такой рез будет не гильотинным (рис. 1: а) – гильотинный рез, b) – не гильотинный рез).
Вообще, не гильотинный рез более эффективен, чем гильотинный, но требует большего пространства поиска и более сложную разделку материала и упаковке алгоритма. Учитывая, что не гильотинный рез является более общим, чем гильотинный, было представлен модифицированный ГА для не гильотинного реза, т.к. параметры данного алгоритм могут быть легко изменены для гильотинного и данный алгоритм может быть так же примирим для решения.
Общая цель задач упаковки является сведение к минимуму уровня отходов. Площадь отходов вычисляется по формуле (1): разница между площадью материала St и суммой площадей N размещенных на нем деталей S i.
Вторым критерием оптимальности является форма полученных отходов. На производстве предпочтительным является отход прямоугольной формы, а не ломаной, т.к. его легче в дальнейшем использовать. Данный критерий выступает коэффициентом С (2), который показывает приближенность фигуры к прямоугольнику. Пусть C w – периметр отходов раскроя, C E – периметр прямоугольника равной по площади с полученной формой отхода. Следовательно С – коэффициент, который показывает разницу между ними.
Наиболее широко используемым простым алгоритмом упаковки является эвристический алгоритм BL. Процесс упаковки алгоритма BL состоит из 2-х шагов. Во первых, упаковка прямоугольников случайным образом. Во-вторых, в соответствии с порядком упаковки, место каждого прямоугольника на раскраиваемом материале определяется максимальным перемещением его вниз и влево в нижней левой точки материала. Hopper и Turton (1999) использует SGA (простой генетический алгоритм) в качестве первого шага BL алгоритма для генерации и оптимизации порядка упаковки, однако, процесс BL упаковки может создать разрывы между упакованным прямоугольниками и такие отходы также не могут быть использованы. Faina (1999) исследовал BL процесс упаковки, чтобы найти его недостатки. Lui и Den (1999) пытались найти алгоритм, при котором пробелы между деталями были бы минимальны. Оба алгоритма улучшают качество решений, но не решают проблему разрыва полностью. В этой статье жадный алгоритм упаковки представлен на основе всех раскроев с целью получить оптимальный с точки зрения раскроя отход. Так же вычислительные результаты показывают, что можно полностью избежать разрывов. Кроме того, универсальная схема кодирования используется, чтобы разносторонне развить популяцию хромосом, адаптивное перекрестное соединение и вероятности мутации, чтобы предотвратить преждевременное решение, и также разработан стохастический оператор преодоления увеличения отхода, чтобы улучшить качество раскроя.
Шаг 1. Предположим, что поколение g = 0. Инициализируем M особей согласно универсальной схеме кодирования. Для любых особей M i и M j, определим Расстояние Хемминга H ij этих двух особей как:
M ik представляет k-й бит i-ой особи. Если H ij< T, тогда удаляем одну из особей – i или j случайным образом, и генерируем новую особь. T - установленный порог. Чем больше T, тем разнообразней генерируется популяция.
Шаг 2. Упаковка и определить качество особей популяции в соответствии с жадным алгоритмом:
1. Инициализировать односвязный список P дополнительных распакованных точек. Первый элемент Р – крайняя левая точка первого прямоугольника p°
2. В порядке упаковки, разместить левую точку прямоугольника на следующей дополнительной р-точке в списке P, и вычислить его фитнес-функцию f i. После всех дополнительных пунктов в списке P рассчитываются, найти наименьшее фитнес функцию f k =min f i и отметить относительно ее точку p k.
3. Установите левую точку прямоугольника на точку p k и удалите p k, и одновременно вставьте в нижней левой точки p k, правой нижней точке p k+1 , и к правой точки p k+2 в список P , затем изменить указатели.
4. Если все прямоугольники уложены, перейти к следующему шагу. Иначе вернуться к пункту 2.
Фитнес функция вычисляется следующим образом: f=αW+βC . Для любой особи, W - коэффициент отходов материала, и С – коэффициент периметров, где α и β являются коэффициентами, связанные с популяцией g. В начале α > 0.9 и β<0,1, после определенного количества поколений, когда коэффициент отходов будет близок к оптимальному решению, необходимо увеличить значение β для рационального использования материала.
Шаг 3. Сделайте выбор отбора для текущей популяции (рулетка и элитарная схема). Вероятность Pi особи i была выбрана в следующем поколении
Сохранить 5%-10% особей с лучшими фитнес-значениями и переместить и в популяцию следующей эпохи.
Шаг 4. Выполнить оператор кроссовера на выбранной популяции. Четыре оператора кроссовера включают: одноточечный кроссовер, чатично отображаемый кроссовер, упорядоченный кроссовер, Non-Able кроссовер.
Шаг 5. Оператор мутации популяции. Были использованы операторы замены и инверсии, вероятность мутации Pm это:
P o- исходное значение, и управляющие параметры, f – среднее значение фитнесс функции, f min – лучшее фитнесс значение, H – среднее значение расстояния Хемминга.
Шаг 6. Если g>gmax gmax или лучший фитнес значение не изменяется в течение 10 поколений, перейти к следующему шагу. Иначе g =g +1, перейти к шагу 2.
Шаг 7. Выведите оптимальное решение.
Тест, разработаный Kofman и Shora (1990), используется для сравнения эффективности различных операторов кроссовера и алгоритм работы Faina (1999). Во-первых, инициализировать параметре материала с шириной W и бесконечной длины, во-вторых, определить количество прямоугольников (от 8 до 64) с шириной и длиной случайным между (0, w). Каждый моделирование работает в 100 раз. Таблица 1 сравнивает четыре оператора кроссинговера, два оператора мутации и стохастического возростания результатов. При сравнении операторов кроссинговера, стохастическое возростание решения используется и при сравнении операторов мутации, при использовании операторов частично отображаемого кроссинговера. Таблица 2 сравнивает эффективность алгоритма, используемого в данной работе и в алгоритме, предложенным Faina (1999).
| Кроссинговер | Среднее % | Мин/Макс % | Мутация | Среднее % | Mин/Макс % |
| Одноточечный | 96.12 | 94.14/96.91 | Обмен | 93.89 | 92.17/95.55 |
| Частично отображаемый | 96.33 | 93.98/97.71 | Инверсия | 94.47 | 92.08/96.13 |
| Порядковый | 96.07 | 93.24/97.32 | SHC | 96.33 | 93.98/97.71 |
| Non-Able | 94.46 | 91.08/97.65 |
| Количество прямоугольников | Среднее % | Mин/Mакс % | Максимальное отклонение % | Среднее % | Mин/Mакс % | Максимальное отклонение % |
| 8 | 92.32 | 90.11/95.28 | 2.94 | 90.31 | 82.34/96.36 | 7.97 |
| 16 | 95.15 | 93.16/97.07 | 1.99 | 92.95 | 87.96/96.91 | 4.99 |
| 32 | 96.33 | 93.98/97.71 | 2.35 | 93.29 | 91.44/94.45 | 1.85 |
| 64 | 93.44 | 91.86/96.21 | 2.77 | 92.29 | 88.56/94.88 | 3.73 |
Вычислительные результаты в Таблице 1 показывают, что кроме оператора Non-ABEL, нет большого различия эффективности среди других трех операторов. Так как оператор Non-ABEL больше походит для случайного поиска,но плохо сохраняет хорошую схему, которая является ключевым в методе ГА, производительность также не устойчива. Что касается операторов мутации, очевидно, что у оператора SHC лучшая производительность. Оператор SHC не только выбирает потомков с более высоким значением приспособленности, но также и принимает особей с более низким фитнесс значением и определенной вероятностью, которая является хорошим примером для комбинации ГА и методов локального поиска окружения, чтобы улучшить производительность.
В Таблица 2, представлена производительность алгоритма, используемого в этой статье и она выше, чем у Faina. После порядка упаковки созданного ГА, используется жадный алгоритм для упаковки прямоугольников в исходный материал и каждый раз получается лучшая карта раскроя. В то время как алгоритм Faina использует алгоритм случайной упаковки, который не гарантирует лучшую карту раскроя, хотя упорядоченная упаковка также эффективна. Кроме того, мин/макс – коэффициент отходов, который был использован в данной статье, очевидно, меньше, чем в алгоритме Faina. Следует отметить, что алгоритм моделирования отжигом, используемый в алгоритме Faina, более чувствителен к начальным значениям в постановке задачи комбинаторной оптимизации.
Yakobs (1996), Hopper и Turton (1999), и Lui и Den (1999) также используют GA, но производительность не может быть сопоставлена, потому что они не указывают форму и размеры исходного материала и прямоугольников, которые они использовали. Так как они используют только простые генетические алгоритмы и нижний левый алгоритма упаковки. Оператор кроссовер и SHC оператора с жадным алгоритмом поиска более эффективным.
После рассмотрения общих вопросов и описания алгоритмов задачи резки и упаковки, в этой статье был предложен улучшенный генетический алгоритм для не гильотинного прямоугольного раскроя. Во-первых, самоадаптивная вероятностная мутация будет предотвращать преждевременную сходимость алгоритма, также сравниваются некоторые часто используемые операторы кроссинговера, и стохастическое самовосхождение к оптимуму операторов ГА, направленных на улучшение локальных возможностей поиска экстремума. Во-вторых, жадный механизм вводится с целью получить хороший образец упаковки, представленный последовательным порядком упаковки данного ГА. Результаты расчетов показывают эффективность этих улучшений.
1. Coffman, E.G. and Jr. P. W. Shor (1990). Average-case analysis of cutting and packing in two dimensions, Eur. J. Operational Research, 44, 134-144
2. Dyckhoff, H. (1990). A typology of cutting and packing problrms. Eur. J. Operational Research, 44, 145-159
3. Faina, L. (1999). An application of simulated annealing to the cutting stock problem. Eur. J. Operational Research, 114, 542-556
4. Farley, A. A. (1988). Mathematical Programming Models for Cutting-Stock Problems in the Clothing Industry. J. Ope. Res. Soc., 39, Vol. 1, 41-53
5. Golden, B.L. (1976). Approaches to the cutting stock problem. AIIE Trans, 8, 265-274