Применение распределенного генетического алгоритма при решении задачи об упаковки в контейнеры
Автор: Ю.А. Бюргер, В.Й. Гнатюк, В.И. Литвиненко, А.А. Ткачук
Источник:[http://vmg.pp.ua/books/КомпьетерыИсети/genetic/ГЕНЕТИЧЕСКОГО.pdf]
Автор: Ю.А. Бюргер, В.Й. Гнатюк, В.И. Литвиненко, А.А. Ткачук
Источник:[http://vmg.pp.ua/books/КомпьетерыИсети/genetic/ГЕНЕТИЧЕСКОГО.pdf]
В статье рассмотрен ряд экспериментов по решению задачи упаковки распределенным генетическим алгоритмом. Рассмотрены результаты сравнительных тестов для различных конфигураций операторов генетического алгоритма.
Комбинаторные оптимизационные задачи об упаковке относят к классу NP-трудных задач [1]. Перспективными для решения данного класса задач являются генетические алгоритмы (ГА) [2]. Популяционная основа ГА позволяет во многих случаях эффективно применять распараллеливание алгоритма в кластерных системах. Для работы в многопроцессорной или распределенной среде необходимо использовать немного отличные от обычных ГА – параллельные генетические алгоритмы (ПГА), которые базируются на классических ГА. По принципам манипулирования популяцией ПГА можно классифицировать как глобальные (мелкозернистые, т. н. “фермер-рабочие”), крупнозернистые (островные) и гибридные. Существуют различные виды крупнозернистых ПГА, обладающих рядом значительных преимуществ: покрытие большого пространства поиска, малая вероятность преждевременной сходимости и устойчивость к сбоям. В данной работе представлено описание применения ГА для решения задачи об упаковке в контейнеры, представлены характеристики нескольких конфигураций ГА на основе параллельных популяций при решении данной задачи.
Задача формулируется следующим образом: Задано конечное 73039, множество U = {u1,u2 ,...,un} “предметов” и “размеры” s(u)∈ [0,1] каждого предмета
u ∈ U (размер предмета представлен рациональным числом); требуется найти такое разбиение множества U на непересекающиеся подмножества U1,U2 ,...,Uk ,
чтобы сумма размеров предметов в каждом подмножестве Ui не превосходила 1 и
чтобы k было наименьшим возможным. Можно считать, что предметы , принадлежащие каждому множеству Ui , упаковываются в один контейнер размера 1, а
цель состоит в упаковке предметов множества U в как можно меньшее число контейнеров . Рассматриваемая задача NP-трудна в сильном смысле [1]. Разработка и
оценка алгоритмов решения данной задачи в общем виде усложняется отсутствиеминформации о глобальном решении задачи (наилучшем разбиении). Однако, в частных случаях могут быть составлены такие исходные данные задачи, что глобальное решение может быть получено аналитическим путём. Для определения эффективности работы ГА воспользуемся одной из таких частных задач. Пусть длина
множества заданных размеров блоков кратна двум, а само множество размеров состоит из неповторяющихся, равномерно распределенных значений, принадлежащих отрезку [0,1]. Для удовлетворения этого условия размер каждого блока s(u j ) должен быть рассчитан по формуле:
При таком распределении размеров блоков всегда можно найти такие два блока, что их суммарный размер составит 1. Очевидно, что при использовании формулы (1) для задания размеров блоков, наилучшая упаковка будет достигнута при разбиении множества блоков на пары (u j ,un-j-1) . Число использованных при этом контейнеров составит n / 2 . Наибольшее число использованных контейнеров совпадает с общим числом блоков n . В дальнейшем будем рассматривать задачу об упаковке в контейнеры для 256 блоков с равномерным распределением размеров. Согласно вышесказанному, лучшее возможное решение такой задачи составит 128 контейнеров.
В ГА каждая из особей оценивается мерой пригодности согласно тому насколько “хорошо” соответствующее ей решение задачи. Наиболее приспособленные особи получают возможность воспроизводить потомство с помощью перекрестного скрещивания с другими особями популяции. Наименее приспособленные особи с меньшей вероятностью смогут воспроизвести потомков. Чтобы использовать ГА, нужно сначала выбрать соответствующую структуру для представления этих решений. Структура данных ГА (особь) состоит из одной или более хромосом. Обычно хромосома представляет собой строку бит, поэтому часто используется термин строка. Каждая хромосома представляет собой объединение определенного числа подкомпонентов, которые называются генами. Гены являются позициями или локусами хромосомы и принимают значения называемые аллелями. Биологический термин генотип относится ко всему генетическому составу индивидуума, и соответствует структуре в ГА. Термин фенотип относится к внешним характеристикам индивидуума и соответствует декодированной структуре в ГА. Чтобы оптимизировать структуру при помощи ГА, нужно назначить некоторую меру качества каждой структуры в области поиска. Эту задачу выполняет функция пригодности. ГА случайным образом генерирует начальную популяцию из L структур. На каждом поколении ГА использует операторы отбора, кроссинговера, мутации и позиционирования. Подробное описание ГА приведено в ряде работ [2, 3, 4, 6].
Используемый нами способ кодирования решений заключался в извлечении из хромосомы информации о последовательности размещения блоков. Конечное решение в этом случае представляет собой некоторую очередь блоков, в соответствии с которой алгоритм размещения упаковывает блоки в контейнеры.
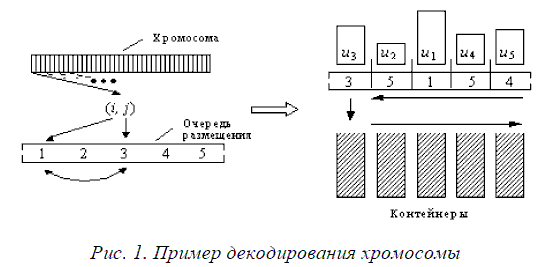
Алгоритм последовательно берет блоки из очереди и помещает их в первый контейнер. При переполнении контейнера происходит переход к следующему свободному контейнеру. При этом очередь обработки блоков извлекается из хромосомы неявно. Процесс декодирования (рисунок 2) выглядит следующим образом. До начала декодирования создадим исходную очередь блоков длины n где каждый элемент указывает на соответствующий тип блока [1,n] и равен своему индексу в очереди (1,2,…,n). Пусть хромосома представлена в виде множества пар (i, j), каждая из которых определяет перестановку в исходной очереди i-го элемента с j-м. Выполнив все перестановки, представленные в хромосоме, получим результирующую очередь размещения блоков. Необходимое для преобразования исходной очереди в любую из возможных количество перестановок легко определяется из следующих соображений. Простейший алгоритм упорядочения данных заключается в приведении произвольной последовательности элементов к возрастающей (или убывающей) последовательности. Для этого простейший алгоритм последовательно просматривает все элементы, начиная с первого, и производит перестановку текущего элемента с минимальным из необработанных (индексы которых выше индекса текущего элемента). Таким образом, каждое конкретное упорядочение может быть рассмотрено как набор перестановок, количество которых равно общему числу упорядочиваемых элементов. Декодирование хромосомы в нашем случае является обратной процедурой упорядочению – начальная возрастающая последовательность преобразуется в одну из возможных последовательностей, что может быть достигнуто исполнением перестановок, полученных при упорядочении, в обратном порядке, начиная с последней. Таким образом, достаточное число перестановок для преобразования исходной очереди в любую из возможных равно числу элементов очереди. Любое решение, полученное описанным образом, является допустимым, что сокращает пространство поиска.
Для задач минимизации (как в нашем случае), значения функции пригодности могут быть инвертированы, а затем перенесены в положительную область для определения пригодности. В случае оценивания недопустимых решений необходимо вводить штрафы или использовать разделенное оценивание, когда допустимым решениям присваивают положительные оценки в соответствии с оптимизируемой функцией, а недопустимым – отрицательные, соответствующие функции “близости” недопустимого решения к области допустимых решений. В рассматриваемой задаче функция пригодности F может быть определена как: F = n-k+1/(k-V2+V1) (2),где k – число задействованных контейнеров; n – общее число блоков; V2 – суммарный размер блоков, находящихся в контейнерах 1… k-1; V1 – суммарный размер блоков контейнера k.
Во всех тестах нами был использован оператор отбора особей на основе элиты. Пусть {a,b,c} соответствуют следующим параметрам ГА: a – оператор кроссинговера (1 – одноточечный, 2 – двухточечный, 3 – равномерный), b – оператор мутации (2 – мутация с заданной вероятностью и плотностью, 3 – мутация с заданной вероятностью и случайной плотностью), c – условие позиционирования особи в популяции (1 – всегда, 2 – только новый генотип, 3 – только новый фенотип). Проведем подбор этих параметров, отмечая качество находимого алгоритмом решения за временной порог в 30 секунд.
| 12 | 22 | 32 | 13 | 23 | 33 | |
| 1 | 98.031 | 99.032 | 103.037 | 101.034 | 100.033 | 95.029 |
| 2 | 99.033 | 100.033 | 98.031 | 102.036 | 102.038 | 100.033 |
| 3 | 103.037 | 103.037 | 103.038 | 104.039 | 104.039 | 106.042 |
Выбираем наилучшую конфигурацию: равномерный кроссинговер, мутация с заданной вероятностью 0.1 и случайной плотностью, в популяцию добавляются только особи с новым фенотипом. Следующий шаг – определение эффективного размера популяции и элиты для оператора отбора.
Наилучшие и практически равные результаты получены при размерах популяции/элиты: 8/8, 32/16 и 512/32. Дальнейший выбор может быть сделан из различных соображений и во многой степени зависит от предпочтений исследователя.
В крупнозернистой модели каждый процессор поддерживает отдельную локальную популяцию, отдельные популяции принято называть островами. Нами было реализовано две топологии параллельного ГА – топология кольцо и полный граф. Критерием качества при этом выступало время поиска решения, не ниже заданного значения функции пригодности (100). Все модели были реализованы средствами языка программирования Visual C++ с использованием интерфейса MPICH под управлением операционной системы Windows 2000. Используемая кластерная система имела следующие характеристики: CPU узла - AMD K6-2+ 550MHz, ресурсы памяти узла – 128Mb, характеристика сети - 100Mbit.
Результаты экспериментов показали, что использование процессоров более трех выигрыша в скорости не дает. Наилучшей конфигурацией оказалась топология кольцо для трех процессоров, при периоде миграций особей 20 циклов. Ускорение поиска по сравнению с ГА для одного процессора составило при этом 1,9.
В результате проведения исследований по решению задачи об упаковке в контейнеры методом распределенных ГА была разработана функция пригодности и способ кодирования генетической информации, удовлетворяющие требованиям задачи. Рассмотренный метод кодирования хромосом является приемлемым для использования в ГА, позволяет находить алгоритму эффективные решения, за счет отсечения заранее не пригодных решений.
1. Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи: Пер. с англ.
– М.:Мир,1982.–416 с.
2. Holland John H.Adaptation in Natural and Artificial Systems:An Introductory Analysis with
Application to Biology, control, And Artificial Intelligence. University of Michigan, 1975.
3.Скурихин А.Н. Генетические алгоритмы // Новости искусственного интеллекта № 4. –
Москва 1995. – С. 6–46.
4. Белкин А.Р., Левин М.Ш. Принятие решений: комбинаторные модели аппроксимации
информации. М.: Наука 1990. 160 с.
5. Whitley D. Starkwheather, T. and K. Mathias. Optimization using distributed genetic algorithms.
In Proceedings of Parallel Problem from Nature, pages 176-184, 1991.