Генетический алгоритм поиска минимума в задачах двумерного гильотинного раскроя
Автор:А.С. Мухачева, А.В. Чиглинцев
Источник:Журнал «Информационные технологии», №3/ 2001
Автор:А.С. Мухачева, А.В. Чиглинцев
Источник:Журнал «Информационные технологии», №3/ 2001
Рассматривается задача гильотинного раскроя рулонного материала. Известны методы расчета оптимального раскроя в условиях массового производства, основанные на линейном программировании с неявным заданием матрицы раскроев. Здесь основной является целочисленная задача раскроя. Для ее решения предлагается генетический гильотинный алгоритм на базе методологии И. П. Норенкова с использованием последовательности эври-стик в качестве аллелей генов.
Предположим, что имеется полубесконечная полоса (рулон) ширины W, а также прямоугольные предметы нескольких типов. Их можно поворачивать на 90 °. Для каждого типа i={1,m}, заданы размеры (wi,li) и их необходимое число bi. Требуется найти гильотинный раскрой рулона на заданные прямоугольные предметы, который обеспечит минимальную длину L' использованной части полосы.
Под гильотинным понимается раскрой, реализуемый последовательностью сквозных резов, параллельных кромкам материала (рис. 1). Эта задача подробно рассматривалась различными авторами [1]. В частности, в работе [2] приведены послойные алгоритмы для задачи гильотинного раскроя в условиях единичного производства.
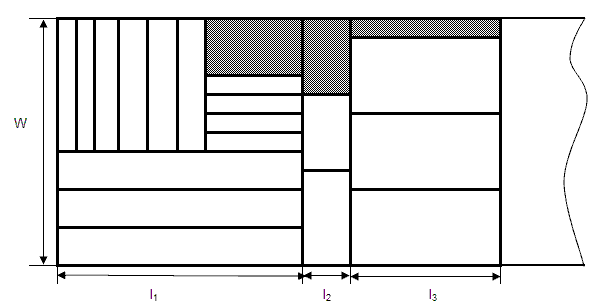
Решение с помощью детерминированного послойного алгоритма с I > I* находится за один проход. При этом возникает эффект "хвоста", когда в конце полосы остаются "плохо" заполненные области.
Этот недостаток частично сглаживается за счет применения оценок прямоугольников аналогично интерпретации двойственных переменных (оценок) Л. В. Канторовича, применяемой в методе последовательного уточнения оценок [3]. Однако практически исправление раскроя происходит только на нескольких первых итерациях, далее процесс оказывается вялотекущим и возможно зацикливание.
В последнее время для решения задач раскроя стали применять различные метаэвристики, которым в меньшей степени присущи указанные недостатки.
В работе приведен генетический алгоритм для решения задачи прямоугольной упаковки (не гильотинного раскроя), основанный на ее блочной структуре. В качестве аллелей используются последовательности перестановок прямоугольных предметов в блоках. Другая интерпретация аллелей в задачах упаковки предложена И. П. Норенковым. Ген означает способ упаковки очередного прямоугольного предмета, аллели – последовательности алгоритмов для его упаковки. Для гильотинного раскроя именно этот подход представляется нам наиболее удобным. Принципиальным здесь оказывается представление структуры гильотинного раскроя как последовательности вложенных друг в друга прямоугольных блоков, именуемых далее корзинами. Последовательность аллелей представляет собой различные алгоритмы типа первый подходящий и жадный алгоритм. В случае случайного выбора алгоритма типа первый подходящий укладывается один или несколько одинаковых прямоугольных предметов и формируется новая корзина, в случае жадного алгоритма заполняется наилучшим образом боковая грань очередной корзины.
В основе генетического гильотинного алгоритма (Genetic Guillotines Algorithm – GGА) лежит следующая идея: основная задача разбивается на Р подзадач, Р – число заполненных корзин. В качестве подзадачи можно рассматривать однородное размещение предметов одного и того же вида в количестве qj, j={1;P}, с помощью одной из эвристик, которые будут описаны ниже, тогда ∑Pj=1 q j=∑mi=1 b i
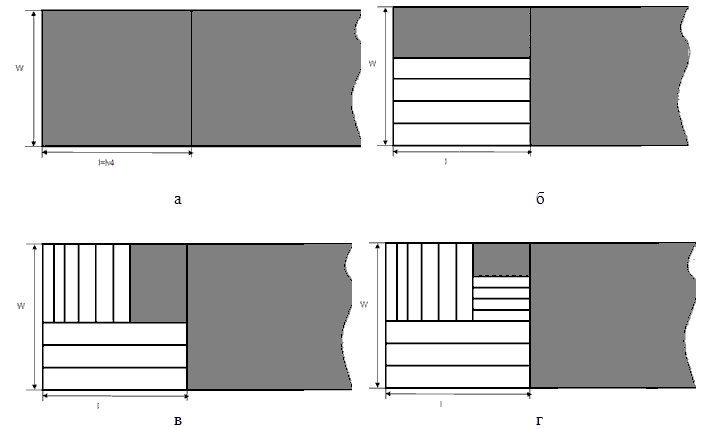
На рис. 2 представлен процесс формирования подзадач и их решения. Начальной корзиной является весь рулон. В приоритетном списке фиксируется предмет типа vi, случайно выбирается алгоритм его раскроя с указанием корзины и направления размещения прямоугольника vi, фиксируется длина. Затем реализуется вертикальный рез, он выделяет корзину с размерами (w, l), w =W, l =lvi (рис. 2, а). Эта корзина разрезается горизонтальными резами на максимально возможное число (в данном случае равное четырем) прямоугольников типа vi и число bvi прямоугольных предметов корректируется с учетом уже полученных.
Размеры новой незаполненной корзины: w =W - 4wvi (рис. 2, б). Для этой корзины определяется новый ведущий прямоугольный предмет с номером v2, его направление и число резов, равное шести (рис. 2, в).
Для следующей корзины с размерами w = W - 4wvi, l= lv1-6lv2 определяется ведущий прямоугольный предмет с номером, направление и число резов, равное четырем (рис. 2, г). Следующая корзина представляет остаток. Далее в качестве новой корзины опять фигурирует полубесконечная полоса.
Процесс продолжается до тех пор, пока все прямоугольные предметы не будут получены. Корзины с одинаковыми прямоугольными предметами формируются согласно случайному выбору алгоритма размещения из заданного списка алгоритмов. Таким образом, выбор способа раскроя для каждого прямоугольного предмета сводится к задаче поиска алгоритма из последовательности заданных эвристик. Случайный перебор решений осуществляется с помощью генетического алгоритма.
Главной особенностью является то, что аллелями служат не значения проектных параметров, а имена эвристик, используемых для определения этих значений. При этом ген j соответствует j-й подзадаче, аллелями являются номера (имена) эвристик. Сформулируем эвристики, с помощью которых решаются подзадачи. Они основаны на очень простых стратегиях и часто приводят к хорошим результатам. Среди них выделяются методы типа первый подходящий (FF) и жадные (Gr) алгоритмы. В свою очередь, среди алгоритмов FF различаются он-лайн алгоритмы, которые рассматривают заготовки в заданном порядке, и офф-лайн алгоритмы, в которых прямоугольники вначале упорядочиваются. Эвристики для решения задач линейного раскроя приведены в работе и адаптированы для двумерного случая.
• First-fit (FF) – первый подходящий. На каждом шаге текущий прямоугольный предмет помещается в частично заполненную корзину с наименьшим порядковым номером, имеющую подходящую остаточную емкость. Если ни одна корзина не удовлетворяет этим условиям, то прямоугольный предмет упаковывается в новую корзину.
• Best-fit (ВF) – лучший подходящий. На каждом шаге текущий прямоугольный предмет сопоставляется той корзине, которая имеет наименьшую допустимую остаточную емкость. Предпочтение отдается корзине с наименьшим порядковым номером. В случае отсутствия таковой берется новая.
• Worst-fit (WF) – худший подходящий. В противоположность "лучшему подходящему" выбирается корзина с наибольшей подходящей остаточной емкостью. Если не существует ни одной, берется новая корзина.
Учет гильотинности состоит в том, что корзины формируются алгоритмически путем сквозных линий, параллельных кромкам рулона. Упаковке очередного предмета предшествует формирование новой корзины, как это показано на рис. 2. Причем, если предметы могут быть ориентированы двумя способами, число эвристик удваивается, т. е. применяется каждая из них с повернутыми на 90° предметами.
• Gridi (Gr) – жадный алгоритм. Сводится к решению очередной задачи 0-1 рюкзак. При этом оптимизация осуществляется по ширине корзины, а длина l заполненной части корзины определяется самым длинным, вложенным в нее прямоугольником. Остатки по длине определяют новые корзины. Например, в соответствии с примером, приведенным на рис. 2, уже на первом этапе будет получен фрагмент, изображенный на рис. 3, здесь w = W - 4wvi , l=l v2-6 l v1(в примере рис. 2,бив потребовалось два этапа). Однако это вовсе не означает предпочтение жадного алгоритма."Жадное" заполнение корзины Для включения в генетический алгоритм был проведен предваритель-ный эксперимент и в результате были отобраны алгоритмы FF, ВF, WF и Gr с учетом поворота предметов на 90°. При этом Gr применялся только для корзин ширины w=W.
Структура хромосомы в генетическом алгоритме выглядит следующим образом: [(h1,q1),(h2,q2),...,(hn,qn)],
где hj – номер эвристики для j-го гена;
qj – числопредметов, размещаемых с помощью данной эвристики hj
Генетические операции кроссовер и мутация можно определить, как в классическом генетическом алгоритме. Однозначное восстановление
раскроя из такой хромосомы подразумевает наличие приоритетного списка номеров прямоугольников, определенного, например, по убыванию площади
предметов.
Функцией приспособленности для особей будет длина занятой части полосы L', полученная после восстановления раскроя. Чем меньше L', тем более приспособленной является особь. Оценить качество полученного раскроя можно с помощью коэффициента раскроя (Cutting Coefficient, СС) k, равного отношению полезной площади ко всей израсходованной.
Структура упаковки представляется в виде линейного списка, состоящего из звеньев следующего вида:(N, x, y, wb,lb, tпр,k),
где N – порядковый номер корзины;
х, у – координаты левого нижнего угла корзины;
wb, lb – ширина и длина корзины;
tпр – тип предмета(номер в приоритетном списке);
k – число размещенных прямоугольных предметов.
Весь список будет иметь вид: Начало→(N1,x1,y1,wb1,lb1,tпр1,k1)→(N2,x2,y2,wb2,lb2,tпр2,k2)→(Ns,xs,ys,wbs,lbs,tпрs,ks)→Конец
В этом списке каждой корзине соответствует одно звено.
1. Мухачева Э.А Рациональный раскрой промышленых материалов.Применение в АСУ. М.:Машиностроение,1984. 176 с.
2. Мухачева Э.А., Верхотуров М.А., Мартынов В.В. Модели и методы расчета раскрои-упаковки геометрических объектов. УФА: Изд-во УГАТУ,1998 с 216.
3. Мухачева Э.А., Мухачева А.С., Чиглинцев А.В. Генетический алгоритм блочной структуры в задачах двумерной упаковки //Информационные технологии. 1999 №11 с. 13-18
4. Норенков И.П. Эвристики и их комбинации в генетических методах дискретной оптимизации //Информационные технологии. 1999 №1 с. 2-7.