Расширение генетического алгоритма комбинирования эвристик для решения задачи прямоугольной упаковки
Автор:А.С. Мухачева, А.В. Чиглинцев
Источник:[http://www.work.vegu.ru/vegu/vestnik/DocLib/Валиахметова.pdf]
Автор:А.С. Мухачева, А.В. Чиглинцев
Источник:[http://www.work.vegu.ru/vegu/vestnik/DocLib/Валиахметова.pdf]
В статье рассматривается задача упаковки прямоугольных объектов в полосу, и в листы (контейнеры). Для ее решения предлагается расширение генетического алгоритма И.П.Норенкова. Дается описание ыультиметодного декодера с расширением перечня простых эвристик.
Ключевые слова: генетический алгоритм, мультиметодный декодер, либеральные эвристики, упаковка объектов в контейнеры, комбинаторные задачи.
Целочисленная задача одномерной упаковки является NP-трудной, и точных алгоритмов полиномиальной сложности пока для нее и других задач, сводящихся к ней, не известно [1]. Поэтому один за другим появляются эвристические и приближенные методы. Среди них бурно развиваются метаэвристики: конструктивные алгоритмы и методы локального поиска. Достойным примером алгоритмов локального поиска являются эволюционные алгоритмы, среди них наивный (1+1)-EA алгоритм и генетический метод [2].
И.П.Норенков предложил для решения задач комбинаторной оптимизации эволюционный алгоритм, в котором генами являются простые эвристики, хромосомами – их последовательности, обновляемые на каждом шаге процесса путем применения генетических операторов [3, с. 2-7].
Известно небольшое число различных технологий конструирования алгоритмов локального поиска, предназначенных для решения за-дачи раскрояупаковки. Среди них выделяются уроенееая [4, p. 410-420],беэуровневая и блочная [2] технологии. Предложенный И.П.Норенковым алгоритм также можно толковать как технологию решения комбинаторных задач.
Мультиметодная технология предполагает применение случайных, из заданного набора, алгоритмов для упаковки лучшей детали [3]. Стратегия мультиметодных алгоритмов направлена на двухстороннюю экономию области упаковки, по длине и по ширине, в отличие от указанных выше уровневых и блочных стратегий одного направления. Основные идеи, применяющиеся в мультиметодной технологии комбинирования эвристик, позволяют предположить, что наиболее эффективным будет их применение при решении задач упаковки в контейнеры. Различие блочных и мультиметодных алгоритмов состоит в процедурах заполнения свободных областей.
С целью улучшения упаковок, полученных с помощью алгоритмов, основанных на приведенных технологиях, применяются многопроходные алгоритмы, в том числе метаэвристики.
Мультиметодный алгоритм конструирования упаковки. Остановимся подробнее на задаче упаковки прямоугольных объектов в полубесконечную полосу фиксированной ширины. Имеются прямоугольная полоса заданной ширины w и неограниченной длины и набор из m прямоугольных предметов заданных размеров: (wi,li),i = {1, m}, где wi – ширина, li – длина стороны. Прямоугольной упаковкой RP назовем размещение прямоугольников в полосе, удовлетворяющее условиям:
• ортогональности – стороны прямоугольников параллельны граням полосы;
• неперекрытия прямоугольников между собой;
• неперекрытия прямоугольников с гранями полосы.
Если длина l занятой части допустимой упаковки полосы достигает минимума, то RP называют оптимальной упаковкой. Исходную информацию для задачи упаковки прямоугольных заготовок в полубесконечную полосу принято задавать вектором (W, m, w, l), w = (w1, w2,..,wm), l = (l 1, l2,..,lm) и приоритетным списком PI = (P 1, P 2,..,Pm), в котором прямоугольники упорядочены по длине. Решение задачи определяет упаковка RP, заданная минимальными координатами (xi;yi),i = {1, m} прямоугольников. Допускается поворот компонентов на 90°. В соответствии с предлагаемым И.П.Норенковым алгоритмом в каждой подзадаче исходной задачи выбирается слева наиболее низкий незаполненный участок полосы и выполняется его заполнение по одной из следующих эвристик:
S1) выбирается еще не упакованная деталь, обеспечивающая минимальный вертикальный зазор gap>0; если gap > 0, то деталь размещается вплотную к тому краю участка, на котором меньше (по абсолютной величине) горизонтальный зазор z; если деталей с gap > 0 нет, то участок ширины a и длины h объявляется пустотелым и заполняется фиктивной заготовкой (рис. 1);
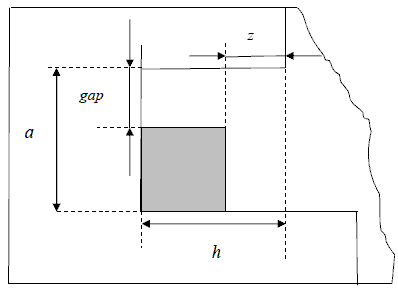
Полученный конструктивный алгоритм является декодером Multi-Method Algorithm (MMA). Он применяется в рамках генетического мультиметодного алгоритма и может быть включен в другие метаэвриетики. В текущей упаковке определяется самая нижняя левая свободная область. Далее к текущей упаковке применяется один из способов укладки – S1-S4. После того как деталь будет упакована, она исключается из списка PI и больше не рассматривается.
Генетические алгоритмы относятся к группе эволюционных алгоритмов. Для них вводятся такие понятия, как ген, хромосома, особь, популяция, поколение, аллель, а также операторы скрещивание, мутация и кроссовер [5]. Приведем характеристику генетического алгоритма для решения задач прямоугольной упаковки.
Традиционный генетический алгоритм (Genetic Algorithm, GA) основан на эволюционных процессах. GA многократно генерирует новые решения Q, применяя операции скрещивания и/или мутации для текущих решений P. Скрещивание генерирует одно или более новых решений, комбинируя два или более текущих решения, а мутация случайно генерирует новое решение.
В качестве кода упаковки (хромосомы) используется перестановка прямоугольников: П = (1[П], 2[П], …, m[П]), где i[П], i = 1, m - индексы прямоугольников. Они идентифицируются как гены. Мы предполагаем, что i[П] имеет знак, который показывает направление размещения прямоугольника i[П] (проектное решение). Аллели генов (+i[П]) и (-i[П]). Каждая родительская пара создает двух новых потомков с помощью оператора скрещивания (crossover).
Мультиметодный генетический алгоритм (Genetic Multi-Method Algorithm, GMA) применяется с описанным выше декодером MMA. Здесь в качестве особи выступает одна упаковка, а применяемые эвристики являются генами. Каждой особиупаковке соответствует единственная последовательность S примененных для ее получения эвристик. Совокупность упаковок образует одну популяцию, несколько популяций – поколение.
Расширение мулътиметодного алгоритма. Разработан мультиметодный декодер (Multi-Method Decoder, MMD), включенный в работу алгоритма И.П.Норенкова, а затем и в эволюционный одноточечный алгоритм (1+1)- ЕА. Основополагающими для его создания послужили идеи И.П.Норенкова, с расширением перечня генов-эвристик, используемых при построении упаковки. Помимо предложенных в оригинальном алгоритме были добавлены следующие:
S5) выбирается еще не размещенная деталь, обеспечивающая минимальный горизонтальный зазор gapR>0 при повернутой ориентации; если gapR > 0, то деталь размещается вплотную к тому краю участка, на котором меньше (по абсолютной величине) вертикальный зазор z; если деталей с gapR > 0 нет, то участок шириной a и высотой h объявляется пустотелым и заполняется фиктивной заготовкой;
S6) выбирается деталь с наибольшей площадью среди еще не размещенных заготовок и с неотрицательным зазором gapR при повернутой ориентации; если таковых нет ереди еще не размещенных деталей, то рассматриваемая область объявляется пустотелой.
Все перечисленные эвристики являются «жадными», и каждая из них выбирает ту заготовку из списка имеющихся неупакованных деталей, которая оставит наименьшее количество незаполненного пространства в горизонтальном или вертикальном направлении или же в смысле площади занятой части рулонного или листового материала. Эвристики S5 и S6 копируют S1 и S4 соответственно, однако их использование позволяет рассматривать детали сначала при повернутой ориентации и лишь при отсутствии подходящей детали – в исходной ориентации.
Далее на базе декодера MMD был разработан мультиметодный декодер с добавлением свободных эвристик (Multi-Method Decoder with Greedy-Free, MMD (GF)). Этот декодер также получен расширением перечня простых эвристик. При работе он использует уже не только эвристики S1-S6, но еще и набор либеральных эвристик, то есть эвристик, свободных от «жадности»:
S1 D) выбирается еще не упакованная деталь, обеспечивающая максимальный вертикальный зазор gap > 0; если gap > 0, то деталь размещается вплотную к тому краю участка, на котором больше (по абсолютной величине) горизонтальный зазор z;
S2D) из неразмещенных деталей с неотрицательным значением вертикального зазора gap выбирается деталь, обеспечивающая максимальный горизонтальный зазор z при исходной ориентации; если таких деталей нет, то делается попытка найти подходящую деталь при повернутой ориентации;
S3D) то же, что и в S2D, но сначала исследуются заготовки при повернутой ориентации;
S4D) выбирается деталь с наименьшей площадью среди еще не размещенных заготовок и с неотрицательным зазором gap;
S5D) выбирается еще не упакованная деталь, обеспечивающая максимальный вертикальный зазор gapR>0 при повернутой ориента-ции; если gapR > 0, то деталь размещается вплотную к тому краю участка, на котором больше (по абсолютной величине) горизонтальный зазор zR;
S6D) выбирается деталь с наименьшей площадью среди еще не размещенных заготовок и с неотрицательным зазором gapR.
Основной идеей, заложенной в описанных эвристиках, является максимизация незаполненного остатка занятой части полосы, т. е. принцип, противоположный «жадности». Введение в рассмотрение такого множества эвристик при конструировании упаковки позволяет уменьшить вероятность застревания алгоритма в локальном оптимуме.
Мультиметодный генетический алгоритм (GMA) построен по мультиметодной технологии. Внутри этого алгоритма могут быть использованы декодеры MMA, MMD, MMD (GF), отличающиеся только наборами задействованных простых эвристик.
Полученные в результате численных экспериментов данные позволяют сделать вывод об эффективности GMA при решении задач раскроя-упаковки на прямоугольные листы, а также рекомендовать к использованию декодер MMD.
При решении задач упаковки в полубесконечную полосу фиксированной ширины алгоритм GMA также позволяет получать хорошие упаковки за короткий временной промежуток. Более того, в ряде задач упаковки, полученные с помощью GMA, не уступают по качеству упаковкам, полученным с помощью других известных алгоритмов. Целесообразна модификация алгоритма GMA с использованием большего числа простых эвристик. Что касается декодера MMA, то его можно рекомендовать для включения в другие алгоритмы локального поиска при решении задач упаковки в контейнеры. Следует отметить, что эффективность алгоритма GMA повышается при включении в его состав декодера MMD.
1. Гэри М., Джонсон Д. Вычислительные машины и трудноразрешимые задачи. - М.: Мир, 1979.
2. Филиппова А.С. Моделирование эволюционных алгоритмов решения задач прямоугольной упаковки на базе технологии блочных структур // Информационные технологии. № 6. 2006.
3. Норенков И.П. Эвристики и их комбинации в генетических методах дискретной оптимизации // Информационные технологии. 1999. №1.
4. Lodi A., Martello S., Vigo D. Heuristic algorithms for three-dimensional bin packing problem // European Journal of Operational Research. 2002. №141.
5. Мухачева А.С., Чиглинцев А.В., Смагин М.А., Мухачева Э.А. Задачи двумерной упаковки: развитие генетических алгоритмов на базе смешанных процедур локального поиска оптимального решения // Информационные технологии. 2001. № 9.