Введение

Скрытые Марковские модели (СMM) – это мощный инструмент статистического моделирования генеративной последовательности, который может быть охарактеризован как процесс генерации наблюдаемой последовательности. СММ нашли применение во многих областях, заинтересованных в обработке сигналов и, в частности обработки речи, а также с успехом применяются на низком уровне NLP-задач. Марков дал свое имя математической теории процессов Маркова в начале ХХ века [3], однако Баум и его коллеги разработали теорию СММ в 1960 г. [2].

Марковские процессы. На рис.1 рассмотрен пример марковского процесса. Представленная схема описывает простую модель фондового рынка. Модель имеет три состояния: Bull, Bear и Even и три индекса наблюдения: up, down и unchanged. Модель представляет собой автомат конечного состояния, с вероятностными переходами между состояниями. Учитывая последовательность наблюдений, например: up-down-down, мы можем легко убедиться, что последовательность состояний была: Bull-Bear-Bear, и вероятность в данном случае равна соответственно 0,2 х 0,3 х 0,3.

Скрытые марковские модели. На рис. 2 показан пример того, как предыдущая модель может стать СММ. Новая модель позволяет выводить все наблюдения символов из каждого состояния с конечной вероятностью. Это изменение делает модель более выразительной.

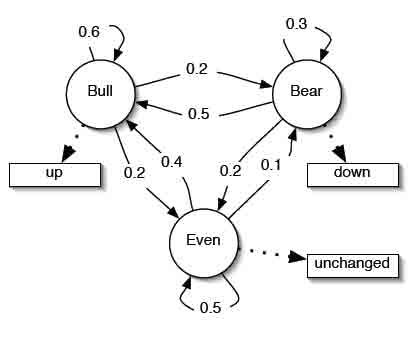
Рисунок 1 – Пример Марковского процесса (1)

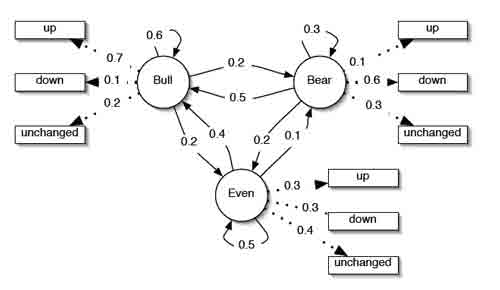
Рисунок 2 – Скрытая Марковская модель (пример 1)

Основное различие в том, что теперь, если мы имеем последовательность наблюдения up-down-down, то мы не можем точно сказать, какая будет последовательность состояний, таким образом последовательность состояний скрыта. Мы можем однако вычислить вероятность того, какая последовательность производится моделью, а также какие могут быть последовательности состояний. В следующих трех разделах описаны общие расчеты и применение СММ.

Формальное определение СMM выглядит следующим образом: λ=(A, B, π).

S – множество состояний алфавита, а V – множество наблюдений алфавита: S=(s₁, s₂, ..., s_N), V=(v₁,v₂, ..., v_M).

Определяем Q – фиксированную последовательность состояний длины T, и соответствующие наблюдения O: Q=q₁, q₂, ..., q_T, O=o₁, o₂, ..., o_T.

Матрица А (не зависит от времени) определяет вероятность перехода из одного состояния в другое состояние: A=[a_ij], a_ij=P(q_t=s_j | q_t-1=s_i).

В – массив наблюдений, сохраняет вероятность наблюдения k, не зависит от t: B=[b_i(k)], b_i(k)=P(x_t=v_k | q_t=s_i).

π – это начальный массив вероятностей: π=[π_i], π_i=P(q₁=s_i).

Существуют два допущения в модели. Первый называется предположение Маркова (текущее состояние зависит от предыдущего состояния). Это представление памяти модели: P(q_t | q₁^t-1)=P(q_t | q_t-1).

Предположение независимости состояния гласит, что очередное наблюдение в момент времени t зависит только от текущего состояния и не зависит от предыдущих наблюдений и состояний: P(o_t | o₁^t-1, q₁^t-1)=P(o_t | q_t).

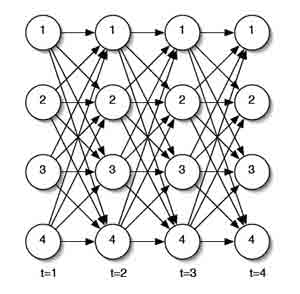
Рисунок 3 – Алгоритм решетки

Оценка

Вероятность наблюдений О в определенной последовательности состояний расчитывается по формуле:

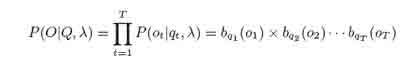
Мы можем вычислить вероятность наблюдений данной модели, как:

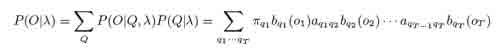
Этот результат позволяет оценить вероятность вывода, но оценивать его непосредственно будет экспонента Т.

Реализуется кэш-решетка состояний на каждом шаге со временем, расчет в кэше оценивается для каждого состояния суммой по всем состояниям на предыдущих шагах со временем. α является вероятностью частичной последовательности наблюдения o₁, o₂, ...o_t и состояние s_i времени t. Это можно представить как на рисунке 3. Определим вероятности для переменной:

В решетку заполняются значения суммы, в последней колонке решетки будет расчитана вероятность последовательности наблюдений. Алгоритм этого процесса называется вперед-алгоритмом и выглядит следующим образом:

1. Инициализация:

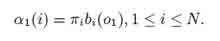
2. Индукция:

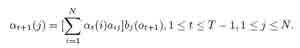
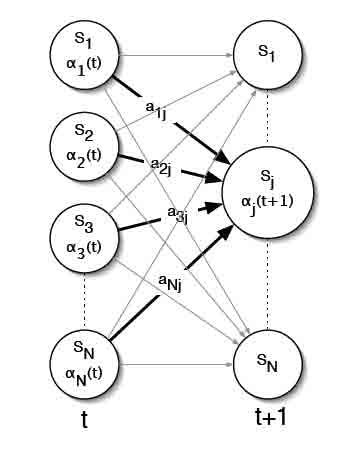
Рисунок 4 – Алгоритм индукции шаг вперед

3. Прекращение:

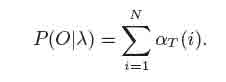
Индукционный шаг ключ к вперед-алгоритму изображен на рисунке 4. Для каждого состояние s_J, α_J(t) сохраняет вероятность того, что состояние заметило последовательность наблюдения до времени t.

Совершенно очевидно, что путем кэширования значений вперед-алгоритм уменьшает сложность. Мы можем также определить аналогичный назад-алгоритм, который является обратным по отношению к вперед-алгоритму, но с обратной переменной: β(i)==P(o_t+1, o_t+2, ... o_T | q_t=s_i, λ), вероятность частичной последовательности наблюдения из t+1 в T, начинается в состоянии s_i.

Декодирование

Целью декодирования является выявление скрытых последовательностей и утверждение, что, скорее всего, имеет место данная последовательность наблюдений. Одним из решений этой проблемы является использование алгоритма Витерби, чтобы найти самую лучшую последовательность наблюдений состояния. Алгоритм Витерби – другая решетка алгоритма, которая очень похожа на вперед-алгоритм, за исключением того, что вероятности перехода максимальные на каждом шагу, а не суммируются. Сначала нужно определить:

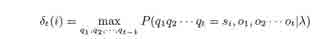
вероятность того, что состояние является наиболее пригодным для частичной последовательности наблюдений.

Алгоритм Витерби выглядит следующим образом:

1. Инициализация:

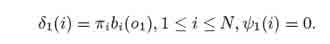
2. Рекурсия:

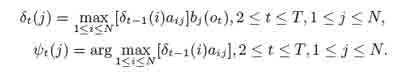
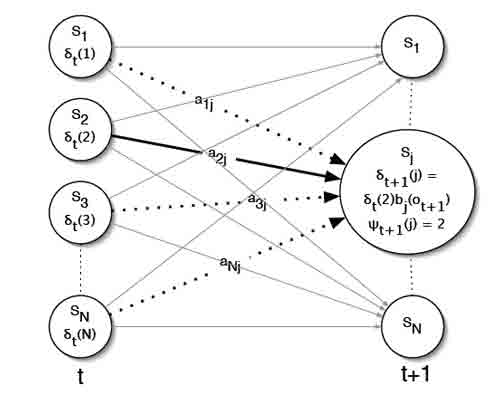
Рисунок 5 – Рекурсионный шаг алгоритма Витерби

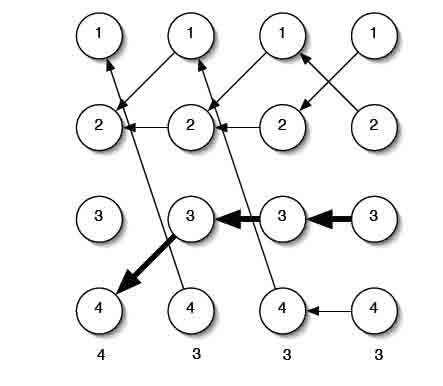
Рисунок 6 – Обратный путь алгоритма Витерби

3. Прекращение:

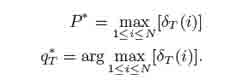
4. Оптимальное состояние обратной последовательности:

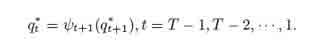
Шаг рекурсии показан на рисунке 5. Основное различие с вперед-алгоритмом в шаге рекурсии, мы максимизируем, а не суммируем предыдущие значения и храним состояние, которое было выбрано в качестве максимального для использования обратного указателя. Обратный шаг показан на рисунке 6.

Обучение

Учитывая множество примеров процесса, хотелось бы иметь возможность оценивать параметры модели λ=(A, B, π), которые лучше всего описывают этот процесс. Есть два стандартных подхода к этай задаче, они зависят от формы примеров и называются контролируемое и неконтролируемое обучение. Если обучающие примеры содержат как входы так и выходы процесса, можно провести контролируемое обучение, но если только входы представлены в подготовке данных, то необходимо использовать неконтролируемую подготовку и угадать модель, которая, возможно, использовала эти наблюдения. В этом разделе рассматривается контролируемый подход к обучению и обсуждается Baum-Welch алгоритм для неконтролируемого обучения.

Самое простое решение для создания модели λ является наличие большого количества обучающих примеров, каждый с аннотацией правильной классификации. Определим два множества:

– t₁, ..., t_N – это набор тегов, который мы приравниваем к набору состояний СMM s₁, ..., s_N

– w₁, ..., w_M – множество слов, которые мы приравниваем к множеству наблюдений СMM v₁, ..., v_M

Для перехода матрицы мы используем:

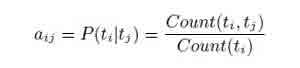
где граф (t_i, t_j) – это номер t_j, который следуют из t_i в обучающих данных. Для наблюдения используется матрица:

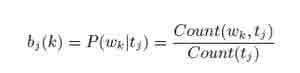
где граф (w_k, t_j) – это номер w_k, который был помечен t_j в обучающих данных. И, наконец, начальное распределение вероятностей:

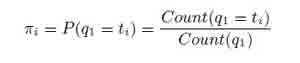
На практике при оценке СMM, как правило, следует применять сглаживание. Во избежание нулевого счета и повышения производительности модели данных не появляются в обучающем множестве.

Многомерное пространство признаков

Ограничение модели в том, что наблюдения считаются одномерными функциями. Но многие задачи наиболее естественно моделируются с помощью многомерного пространства признаков. Одним из решений этой проблемы является использование полиномиальной модели, которая предполагает, что особенности наблюдения являются независимыми [4]:

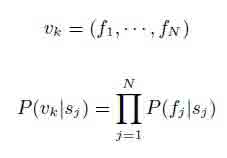
Эта модель проста в реализации и вычислительно не сложна, но очевидно, что многие черты, которые можно было бы использовать, не являются независимыми. Для многих систем NLP было установлено, что недостатки Baysian предположения независимости могут быть очень эффективными.

Применение СММ

Реализации СMM с плавающей точкой является серьезной проблемой. Очевидно, что при применении алгоритма Витерби или вперед-алгоритма для длинных последовательностей крайне малы значения вероятности, что может привести к затруднению реализацию на большинстве машин. Решается эта проблема по-разному для каждого алгоритма:

Т. к. Витерби алгоритмы только увеличивают вероятность, простым решением является суммировать значения всех вероятностей, а не умножать. В самом деле, если все значения матриц в модели (A, B, π) хранятся в журнале, то во время выполнения необходимы только операции сложения.

Для вперед-алгоритма суммировать вероятности не является решением данной задачи. Наиболее распространенное решение этой проблемы заключается в использовании коэффициентов масштабирования, которые содержат вероятности значения в динамическом диапазоне машин и зависят только от t. Коэффициент с_t находится по формуле:

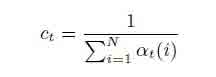
аналогичный коэффициент α может быть вычислен по:

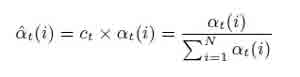
налогичный коэффициент может быть вычислен и для β_t (i).

Список использованной литературы

1. Huang et. al. Spoken Language Processing. Prentice Hall PTR.
2. L. Baum et. al. A maximization technique occuring in the statistical analysis of probablistic functions of markov chains. Annals of Mathematical Statistics, 41:164–171, 1970.
3. A. Markov. An example of statistical investigation in the text of eugene onyegin, illustrating coupling of tests in chains. Proceedings of the Academy of Sciences of St. Petersburg, 1913.
4. A. McCallum and K. Nigram. A comparison of event models for naive bayes classification. In AAAI-98 Workshop on Learning for Text Categorization, 1998.
5. L. Rabiner. A tutorial on hidden markov models and selected applications in speech recognition. Proceedings of IEEE, 1989.