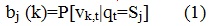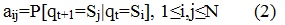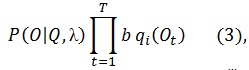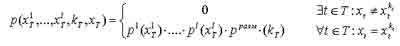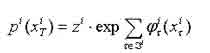На сегодняшний день бесплодие является актуальной проблемой, которая затрагивает около 10% супружеских пар. В настоящее время широкое распространение для лечения бесплодия получило применение экстракорпорального оплодотворения (ЭКО), больше известного как «ребенок из пробирки». При подготовке к ЭКО значительную роль играет УЗИ. С помощью УЗИ проводится диагностика состояния полости матки, определение числа антральных фолликулов. При таком исследовании можно также выявить полипы, синэхии, участки эндометриоза. Для получения хороших результатов после обнаружения подобных патологий необходимо сначала провести лечение, а потом начинать цикл ЭКО. На изображении патологии представляют собой участки пониженной и повышенной эхогенности.

Однако, несмотря на большое количество существующих компьютерных систем обработки изображений, системы для исследования изображения полости матки при подготовке к ЭКО не разработаны. Поэтому необходимо создание специализированной компьютерной системы «ЭКО» (СКС), которая будет обрабатывать изображение, полученное при исследовании и ставить предварительный диагноз.

СКС анализирует изображение, полученное с аппарата УЗИ Aloka SSD 3500. Это универсальный цветной диагностический сканер. Программное обеспечение СКС для обработки изображения разрабатывается на языке программирования Visual Basic 6.0.

Основными методами обработки изображения, используемыми в СКС, выбраны Марковские модели, которые являются мощным средством моделирования различных процессов и распознавания образов. По своей природе Марковские модели позволяют учитывать непосредственно пространственно-временные характеристики сигналов, и поэтому получили широкое применение в распознавании речи, а в последнее время – изображений [1].

Проведен анализ существующих Марковских моделей и исследованы возможности их применения для решения поставленной задачи. Исходя из этого, для обработки изображения УЗИ выбраны: Марковские случайные поля, скрытые Марковские модели первого порядка, древовидные Марковские модели, Марковские цепи.

Каждая модель λ=(A, B, π) представляет собой набор N состояний S={S₁, S₂,…, S_N}, между которыми возможны переходы.

В каждый момент времени система находится в строго определённом состоянии. При переходе в каждое состояние генерируется наблюдаемый символ, который соответствует физическому сигналу с выхода моделируемой системы. Набор символов для каждого состояния V={v₁, v₂,…, v_M}, количество символов M.

Символ в состоянии q_t=S_j в момент времени t генерируется с вероятностью:

Набор всех таких вероятностей составляет матрицу B={b_j(k)}, где b_j(k) – вероятность выпадения k-го значения параметра в j-м состоянии.

Матрица A={a_ij} определяет вероятность перехода из одного состояния в другое состояние:

Считается, что A не зависит от времени.

Также модель имеет вероятность начальных состояний π=π_i, где π_i=P[q₁=S_i] – вероятность того, что в начальный момент система окажется в i-м состоянии.

Модель λ=(A, B, π) с настроенными параметрами может быть использована для генерирования последовательности наблюдений. Для этого случайно, в соответствии с начальными вероятностями π выбирается начальное состояние, затем на каждом шаге вероятность B используется для генерации наблюдаемого символа, а вероятность A – для выбора следующего состояния. Вероятность P генерирования моделью λ последовательности состояний O:

где Q=q₁, q₂,…,q_T – последовательность состояний.

Предполагается, что наблюдения статистически независимы.

В распознавании образов скрытые Марковские модели применяются следующим образом. Каждому классу i соответствует своя модель λ. Распознаваемый образ (изображение) представляется в виде последовательности наблюдений O. Затем для каждой модели λ вычисляется вероятность того, что эта последовательность могла быть сгенерирована именно этой моделью. Модель λ_j, получившая наибольшую вероятность, считается наиболее подходящей, и образ относят к классу j.

Для текстурной сегментации изображения может быть использовано Марковское случайное поле. Текстурным изображением x_T назовем изображение, полученное в результате следующего случайного процесса. Независимо друг от друга генерируются l изображений x¹_T, x²_T, ..., x^l_T и размера k_T в соответствии с распределением p¹(x_T), p²(x_T), ..., p^l(x_T) и p^разм(k_T) соответственно. Далее текстурное изображение x_T строится из полученных изображений согласно следующему правилу: если пиксел t разметки имеет метку k₁∈K={1,2, ..., l}, то в соответствующий пиксел x_t результирующего изображения переносится цвет из изображения k-ой текстуры x^k_T. Точнее, цвет x_t каждого пиксела вычисляется по формуле: ∀_t∈T:x_t=x_t^k.

Из построения следует формула для совместного распределения вероятностей изображений x¹_T, x²_T, ..., x^l_T:

Распределение вероятностей i-й текстуры xⁱ_T задается формулой:

Рассмотренные Марковские модели для обработки изображений обладают оптимальными свойствами и позволяют обнаружить патологии полости матки. На основе этих моделей были проведены исследования и получены хорошие результаты. Предполагается, что разработанная СКС поможет врачу поставить максимально правильный диагноз и назначить соответствующее лечение при подготовке пациентки к циклу ЭКО.

Список использованной литературы

1. International Telecommunication Union [Electronic resource]/ Интернет-ресурс – Режим доступа: http://www.lampai.tsure.ru/publications/goncharov/Goncharov%20-%20Face%20Detection%20and%20Recognition.pdf
2. Ковтун, И.В. Текстурная сегментация изображений на основании марковских случайных полей [Electronic resource]/ Интернет-ресурс – Режим доступа: http://irtc.org.ua/image/Files/kovtun/kovtun_usim_2003(4)_rus.pdf