Жарких А.А. - Обработка изображений на основе вейвлет-преобразования в базисе Хаара над конечным полем нечетной характеристики

Аннотация

Жарких А.А. Обработка изображений на основе вейвлет-преобразования в базисе Хаара над конечным полем нечетной характеристики. В работе представлен алгоритм вейвлет-преобразования в базисе Хаара над полем Галуа нечетной характеристики. Предложена также методика его использования в обработке изображений формата BMP. Представлены результаты применения этого преобразования к строкам полноцветного изображения. Обсуждаются перспективы использования методики для аудио, видео и текста.

Ключевые слова: кратномасштабный анализ, вейвлеты, конечные поля, обработка изображений.

Введение

В современной теории и практике сигналов активно используются сигналы специального вида – вейвлеты. Они показали свою эффективность в спектральном анализе и сжатии сигналов.

В работах (Чуи, 2001; Яковлев, 2003) можно ознакомиться с теорией и практическими применениями различных вейвлетов. Работы (Fekri et al., 1999; 2002; Oliveira et al., 2002; Phoong, Vaidyanathan, 1997) достаточно подробно освещают современное состояние теории вейвлетов над конечными полями (полями Галуа). В данном сообщении рассматривается простое в реализации преобразование Хаара и обсуждаются особенности его использования над конечными полями.

Практически важные вейвлеты традиционно определяются как функции одной вещественной переменной с вещественными значениями. В зависимости от математической модели (структуры области определения, структуры области возможных значений и вида преобразований) различают дискретные и непрерывные вейвлеты. Так как разложение сигналов в базисе вейвлетов осуществляется с использованием арифметики с плавающей точкой, то возникают ошибки, величина которых зависит от степени приближения сигнала.

Критерии оценки качества работы любой информационной системы субъективны. Тем не менее, можно выделить два основных аспекта в оценке ее качества:

- качество передачи, приема, хранения и обработки информации;

- качество восприятия информации человеком.

Эти аспекты оценки качества не тождественны. Если конечным потребителем информации является человек, то в систему необходимо включать интерфейс адаптации информации к человеческому восприятию.

Передача, прием, хранение и обработка информации могут осуществляться с потерями и без потерь. Человеку безразлично, существуют потери или нет, если он не обнаруживает их с помощью своих органов чувств. При автоматическом функционировании системы без участия человека важно свести любые потери к минимуму, или вообще устранить некоторые из них.

Можно выделить два основных вида потерь:

потери, обусловленные каналами передачи и элементами памяти;

Вейвлеты Хаара представляют собой кусочно-постоянные функции, принимающие два значения {-1; +1}, и заданные на конечных интервалах различных масштабов. Вейвлет Хаара единичного масштаба и нулевого смещения (материнский вейвлет Хаара) – это функция, равная +1 на интервале [0; 1/2) и -1 на интервале [1/2; 1). Вейвлеты Хаара хорошо зарекомендовали себя в практических задачах обработки дискретных сигналов, таких, как массивы отсчетов аудиосигналов и цифровые фотографии.

В традиционной постановке вейвлет-преобразование в базисе Хаара заключается в линейном преобразовании вектора a четной размерности 2M в другой вектор b такой же размерности согласно следующим соотношениям:

(1)

Так как применение преобразования (1) требует увеличения разрядов в дробной части компонент, то оно приводит к необходимости увеличения объема памяти для хранения каждой компоненты вектора-образа по сравнению с компонентой вектора-прообраза. Альтернативный вариант сводится к округлению результатов вычислений (1) так, чтобы вектор-образ занимал в памяти такой же объем, как и вектор-прообраз. Такое требование приводит к ошибке вычислений и потерям при обратном восстановлении вектора-прообраза согласно следующим соотношениям:

(2)

Как правило, в практических задачах, компоненты векторов прообраза и образа соответствуют интенсивности каких-либо колебаний, которая по определению неотрицательна. В результате применения первого из соотношений (1) получается неотрицательная компонента вектора образа. В результате же применения второго из соотношений (1), полученная компонента вектора образа может оказаться отрицательной. Невозможность физической интерпретации отрицательных компонент вектора образа является существенным ограничением практического использования преобразований (1).

Математическое описание преобразования

Один из возможных вариантов разрешения указанных проблем заключается в переходе к арифметике, допускающей точные вычисления без округлений и не требующей увеличения объема памяти в случае преобразования (1). Это арифметика поля Галуа GF(p) или его расширения s-й степени (p – простое число, характеристика поля; s – степень расширения поля). В силу того, что (1) имеет простую структуру, свойства мультипликативной группы расширения поля Галуа не используются, и поэтому достаточно рассмотреть поле GF(p). Для любого простого p существует представление, когда все элементы GF(p) неотрицательны. Кроме того, по определению поля, каждый его ненулевой элемент имеет обратный.

Так как в большинстве компьютеров и систем цифровой связи используется двоичная арифметика, то предпочтительно было бы выбрать p = 2. Однако в поле GF(2) преобразования (1) бессмысленны, т.к. элемент 2 не имеет обратного. Поэтому выбирается нечетное p.

При переходе к полю GF(p) с нечетным p, соотношения (1) можно переписать следующим образом:

(3)

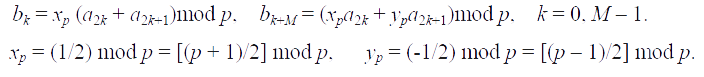
Соотношения (2) можно в данном случае можно переписать следующим образом:

(4)

В преобразованиях (3) и (4) элементы образа и прообраза являются элементами GF(p).

Таким образом, представлен вариант дискретного вейвлет-преобразования Хаара, удовлетворяющий следующим свойствам:

- преобразование (3) осуществляется абсолютно точно;

- объемы памяти, требуемые для хранения входного и выходного векторов, одинаковы;

- все компоненты входного и выходного векторов неотрицательны;

обратное преобразование (4) осуществляется абсолютно точно;

- преобразование (3) не согласовано с восприятием человека, и поэтому некоторые компоненты выходного вектора могут восприниматься как артефакты;

- в силу точности преобразования (4), восстановленный вектор не только воспринимается человеком как идентичный исходному, но и имеет битовый состав, идентичный исходному.

Методика применения алгоритма к BMP-изображениям и результаты моделирования

Каждый пиксель изображения в формате BMP может быть представлен в двоичной системе счисления. Это разложение определяет число бит (N, обычно N = 1, 8, 24) и конкретные их значения Jk для хранения каждого пикселя.

(5)

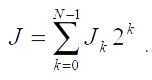
Для применения вейвлет-преобразования над полем GF(p) каждый пиксель изображения в формате BMP должен быть представлен в p-ичной системе счисления. Это разложение определяет число p-ичных цифр и их конкретные значения, используемые в вейвлет-преобразовании.

Рисунок 1 – Исходное изображение «Водяные лилии»

Рисунок 2 – Исходное изображение после вейвлет-преобразования по строкам в базисе Хаара над полем GF(3)

Рисунок 3 – Исходное изображение после вейвлет-преобразования по строкам в базисе Хаара над полем GF(7)

Рисунок 4 – Исходное изображение после вейвлет-преобразования по строкам в базисе Хаара над полем GF(13)

(6)

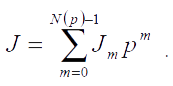
Алгоритм построчного вейвлет-преобразования изображения осуществляется по следующей методике:

а) каждый пиксель изображения раскладывается согласно (6) на p-ичные цифры;

б) ко всем p-ичным цифрам с одинаковыми номерами применяется преобразование (3);

в) p-ичные цифры результата преобразования сворачиваются в одно число согласно (6).

Алгоритм обратного построчного вейвлет-преобразования изображения осуществляется по аналогичной методике с заменой (3) на (4).

Алгоритмы прямого и обратного преобразований по столбцам реализуются аналогично.

Для апробации работоспособности алгоритмов преобразований был использован стандартный полноцветный рисунок Windows в формате BMP «Водяные лилии». Моделирование проводилось в пакете Matlab 7.0. Преобразование осуществлялось по одинаковой схеме параллельно для всех цветовых компонент. Преобразованные изображения также сохранялись в формате BMP. Для уменьшения размера результирующего файла, перед внедрением в текст статьи все изображения сохранялись заново в формате JPEG. Некоторые результаты моделирования представлены на рис. 1–4. Изображения, полученные в результате обратного преобразования, не приводятся, так как полностью совпадают с исходным.

Заключение

В статье рассматривается дискретное вейвлет-преобразование в базисе Хаара над конечным полем нечетной характеристики, которое является модификацией вещественного вейвлет преобразования в базисе Хаара. Последнее хорошо зарекомендовало себя в спектральном анализе и сжатии сигналов различной физической природы.

На основе рассмотренного преобразования можно осуществлять сжатие аудиосигналов для экономного хранения в памяти и качественной передачи по каналам связи, а также для сокращения пространства признаков в системах автоматического распознавания аудиосигналов.

Вейвлет-преобразование в базисе Хаара используется в стандарте JPEG2000 для сжатия изображений с потерями и без потерь. Однако свободно распространяемая информация об этом стандарте ограничена патентом. Вследствие этого невозможно детально сравнить стандарт JPEG2000 со стандартом JPEG и другими стандартами сжатия. Это обстоятельство является подтверждением актуальности данной работы, в которой реализуются дискретные вейвлет-преобразования без потерь на основе арифметики конечного поля.

С практической точки зрения, сжатие видеоинформации необходимо во многих современных радиотехнических системах. В радиолокационных системах сжатие используется для удобства хранения информации об обнаруженной цели. В системах видеонаблюдения сжатие является основой оперативной записи изменений изображения наблюдаемого объекта. В радионавигационных системах на основе сжатия реализуется визуализация цифровых карт с различным разрешением.

Указанные задачи могут быть решены на основе методики точных преобразований без потерь, рассмотренной в данной статье. Результаты моделирования подтверждают работоспособность алгоритмов вейвлет-преобразования.

Рассмотренное преобразование может быть использовано в различных задачах цифровой обработки сигналов. По-видимому, оно будет эффективно в системах многоскоростной обработки данных и мультимедийных системах, использующих TRIPLE-технологии. Это связано с точностью арифметики конечного поля GF(p), которая позволяет обрабатывать не только измеренные физические данные, такие, как аудио и видео, но и точно записанные данные, такие, как текст.

Литература

1. Fekri F., Mersereau R.M., Schafer R.W. Theory of paraunitary filter banks over fields of characteristic two. IEEE Transactions on Information Theory, v.48, p.2964-2979, 2002.
2.Fekri F., Mersereau R.M., Schafer R.W. Theory of wavelet transform over finite fields. Proceedings of the Acoustics, Speech, and Signal Processing (ICASSP), v.03, p.1213-1216, 1999.
3. Oliveira de H.M., Falk T.H., Tavora R. Wavelet decomposition over finite fields. Journal of the Brazilian Telecom. Society, v.17, N 1, p.38-47, 2002. [Portuguese]
4. Phoong See-May, Vaidyanathan P.P. Paraunitary filter banks over finite fields. IEEE Transactions on Signal Processing, v.45, p.1443-1457, 1997.
5. Чуи Ч. Введение в вейвлеты. М., Мир, 412 с., 2001.
6. Яковлев А.Н. Введение в вейвлет-преобразования. Учеб. пособие. Новосибирск, Изд-во НГТУ, 104 с.,2003.