Аннотация
Amara Graps Сопоставление вейвлет и Фурье преобразования Рассмотрены и проилюстрированы сходства и различия методов быстрое преобразование Фурье и дискретного вейвлет–преобразования. Проведен сравнительный анализ этих двух способов частотно–временного разложения сигналов.
Сходство между Фурье и вейвлет
Быстрое преобразование Фурье (БПФ) и дискретное вейвлет-преобразование (ДВП) являются линейными операциями, которые создают структуру данных, которая содержит 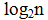 сегменты различной длины, как правило, заполняя и превращая их в различные векторы данных длинной
сегменты различной длины, как правило, заполняя и превращая их в различные векторы данных длинной 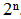 .
.
Математические свойства матриц, участвующих в преобразованиях очень похожи. Обратная матрица преобразования для БПФ и ДВП является транспонированной матрицей оригинала. В результате, оба преобразования можно рассматривать как поворот в пространстве функций на другую плоскость. Для быстрого преобразования Фурье, эта новая плоскость содержит базисные функции, которые являются синусами и косинусами. Для вейвлет–преобразования, эта новая плоскость содержит более сложные базисные функции, которые называются вейвлетами, материнскими вейвлетами, или вейвлет–анализом.
Оба преобразования имеют еще одно сходство. Базисные функции локализованы в частоте, что делает математические инструменты, такие как спектры разложения (сколько размахов содержится в частотном интервале) и скаллограммы (будут определены позже) полезными при расчете частоты и размаха распределения.
Различия между Фурье и вейвлет
Самое интересное различие между этими двумя видами преобразований состоит в том, что частные вейвлет функции локализованы в пространстве, а Фурье функции – синус и косинус – нет. Эта особенность локализации, а также локализация частоты вейвлетов, заставляет многие функции и операторы, использовать «разбросанные» вейвлеты, при преобразовании в вейвлет плоскости. Эта разбросанность, в свою очередь, приводит к ряду полезных приложений, таких как сжатие данных, выявление особенностей в образах, и удаление шума из временных рядов.
Одним из способов узнать частотно–временные различия между преобразованием Фурье и вейвлет–преобразованием, является посмотреть на базисную функцию. Нанесенную на частотно–временную плоскость. На рисунке 1 показанно оконное преобразование Фурье, где окном является простая квадратная волна. Окно квадратной волны обрезает синус или косинус, чтобы соответствовать окну определенной ширины. Так как одно окно используется для всех частот в ДВП, точность анализа остается постоянной на всех участках в частотно–временной плоскости.
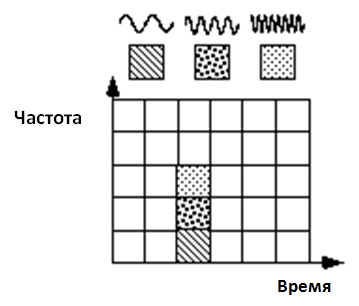
Рис. 1. Базисные функции Фурье, частотно–временные плитки и охват частотно–временной плоскости.
Преимуществом вейвлет преобразования является то, что окна изменяются. Для того чтобы выделить разрывы сигнала, хотелось бы иметь некоторые очень короткие базисные функции. В то же время, для того, чтобы получить подробный анализ частоты, хотелось бы иметь некоторые очень длинные базисные функции. Одним из способов достижения этого является наличие коротких высокочастотных базисных функций и длинных низкочастотных. Эта золотая середина именно то, что вы получаете используя вейвлет–преобразования. Рисунок 2 показывает охват частотно–временной плоскости с одной вейвлет функцией, вейвлетом Добеши.

Рис. 2. Базисные функции вейвлета Добеши, частотно–временные плитки и охват частотно–временной плоскости.
Единственное, что следует помнить это то, что вейвлет–преобразования не имеют единого набора базисных функций, таких как преобразование Фурье, которое использует только функции синус и косинус. Вместо этого, вейвлет–преобразования имеют бесконечное множество возможных базисных функций. Таким образом, вейвлет–анализ обеспечивает немедленный доступ к информации, которая может быть скрыта от других частотно–временных методов таких, как анализ Фурье.
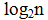 сегменты различной длины, как правило, заполняя и превращая их в различные векторы данных длинной
сегменты различной длины, как правило, заполняя и превращая их в различные векторы данных длинной 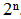 .
.
