Выделение контуров на изображении
Авторы: Скобцов Ю.А., Родин Ю.В., Оверко В.С.
Источник: Моделирование и визуализация поведения потоков крови при патологических процессах. — Донецк: Издатель Заславский А.Ю., 2008. — 212 с., с. 165‒166.
Вычисление первой производной цифрового изображения основано на различных дискретных приближениях двумерного градиента. По определению, градиент изображения f (x, y) в точке (x, y) — это вектор.
Направление вектора градиента совпадает с направлением максимальной скорости изменения функции f в точке (x, y). Важную роль при обнаружении контуров играет модуль этого вектора, который обозначается delta f:
Направление вектора градиента также является важной характеристикой. Вычисление градиента изображения состоит в получении величин частных производных df/dx и df/dy для каждой точки [3]. Это достигается использованием маски 3 х 3, которая задается следующим выражением:
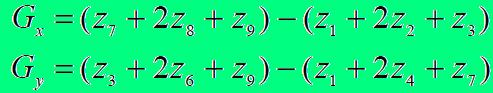
соответствующим маскам, представленным на рис. 4.11.
Рисунок 4.11 — Окрестность 3 х 3 внутри изображения
Увеличенное значение для двух средних элементов используется для уменьшения эффекта сглаживания за счет придания большего веса средним точкам. Для реализации двух последних выражений используются маски, соответствующие оператору Собела.
Рассмотренные маски применяются для получения составляющих градиента 
и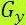 
. Для вычисления величины градиента эти составляющие необходимо использовать совместно. Часто применяется подход, при котором величина градиента вычисляется приближенно через абсолютные значения частных производных:
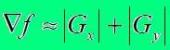
Результат обработки описанным способом представлен на рис. 4.12б.
Рисунок 4.12: а) исходные изображения; б) изображения после обработки
Список использованной литературы
- Скобцов Ю.А. Исследования поведения потоков крови и компьютерная диагностика сосудистых заболеваний // Энергия инноваций / Ю.А. Скобцов, В.С. Оверко, Ю.В. Родин, В.Ю. Скобцов, В.К. Гринь, А.А. Штутин — 2005. — № 2‒3. — с. 40‒42.
- Скобцов Ю.А. Моделирование и визуализация потоков крови в сосудах с различной патологией // Праці Першої міжнародної науково-технічної конференції “Моделювання і комп’ютерна графіка” / Ю.А. Скобцов, В.С. Оверко, Ю.В. Родин — Донецьк, 04‒07 жовтня 2005 р.
- Гонсалес Р. Цифровая обработка изображений в среде MATLAB [Текст] / Р. Гонсалес, Р. Вудс, С. Эддинс — Москва: Техносфера, 2006. — 616 с и др.