Помехоподавление в ЭКГ сигналах с использованием алгоритма адаптивной фильтрации

Авторы: Chinmay Chandrakar, Kowar M.K.

Перевод: Ткаченко С.В.

Год: 2012

Источник: Open System Resuorces Online

Аннотация:
Одной из основных проблем электрокардиографии, со стороны области биомедицинской обработки данных, является отделение полезного сигнала от помех вызванных ЛЭП помехами, внешними электромагнитными полями, случайными движениями тела и дыхания. В данный момент, для очистки сигнала от нежелательных частотных диапазонов применяются различные типы цифровых фильтров. Однако, для уменьшения помех биомедицинских сигналов трудно применять фильтры с фиксированными коэффициентами, потому что поведение человека нельзя в точности предсказать. Адаптивная фильтрация является техникой, необходимой для преодоления этой проблемы. В этой статье представлены несколько типов адаптивных фильтров, предназначенных для снижения уровня помех в ЭКГ сигналах, например, PLI и фильтрации с базовой линией помех. Представлены результаты моделирования работы фильтров в MATLAB. В данной статье используется рекурсивный метод наименьших квадратов (RLS). RLS алгоритм предлагается использовать для удаления артефактов из низких частотных составляющих сигнала. Алгоритм наименьших квадратов направлен на минимизацию суммы квадратов разницы между полезным сигналом и моделью выходного фильтра. Когда новые образцы входных сигналов поступают на каждой итерации, решение проблемы нахождения для них наименьших квадратов может быть вычислено в рекурсивной форме, в результате рекурсивного вызова алгоритма наименьших квадратов (RLS). RLS алгоритмы, как известно, обладают быстрой сходимостью, даже для случаев когда значения корреляционной матрицы входного сигнала велики. Эти алгоритмы имеют отличную производительность при работе в нестационарных условиях. Все эти преимущества неизбежно сопровождаются повышением вычислительной сложности и некоторыми проблемами со стабильностью, но эти проблемы не критичны для алгоритмов основанных на LMS.
Ключевые слова: ЭКГ сигнал, условия Дирихле, адаптивный фильтр.

1. ВВЕДЕНИЕ
Снятие ЭКГ сигналов с высоким разрешением, загрязненных фоновыми помехами, является важным вопросом для проведения исследований. Целью этих исследований является улучшение сигнала ЭКГ. Для облегчения точной интерпретации ЭКГ необходимо отделить допустимые компоненты сигнала от нежелательных артефактов. Многие подходы для этого были описаны в литературе для улучшения ЭКГ с использованием адаптивных фильтров [1] - [3]. Такие фильтры позволяют обнаруживать различные потенциалы времени и отслеживать динамические изменения сигналов. В работах [4] - [6] предложен адаптивный фильтр, основанный на LMS, для периодического получения импульсного отклика нормальных комплексов QRS. Затем данный фильтр применяется для обнаружения аритмий в амбулаторных записях ЭКГ. Входы в алгоритм LMS являются детерминированными функциями и определяются периодическими расширениями, которые, в свою очередь, являются усеченным набором ортонормированных базисных функций.
В этих работах, алгоритм LMS работает на основе мгновенного базиса, такого, как вес вектора, который обновляется для каждого нового образца, на основе мгновенной оценки градиента. Есть определенные клинические приложения обработки сигналов ЭКГ, которые требуют адаптивных фильтров с большим числом запусков. В таких случаях обычный алгоритм LMS неприемлем из-за высоких требований к вычислительным ресурсам. LMS алгоритм и NLMS (нормированный LMS) алгоритмы требуют несколько расчетов, и, следовательно, широко применяются для акустических эхо подавителей. RLS (рекурсивный алгоритм наименьших квадратов) алгоритм, сходимость которого не зависит от входного сигнала, является самым быстрым из всех традиционных адаптивных алгоритмов. Основным недостатком алгоритма RLS являются большие вычислительные затраты. Тем не менее, в последнее время, разработаны быстрые RLS алгоритмы. В этой статье мы хотим получить более быстрый алгоритм, включающий знания номера импульса в алгоритм RLS. В отличие от NLMS и других проекционных алгоритмов, RLS алгоритм не имеет скалярного размера шага. Таким образом, изменение характеристик сигнала ЭКГ не может быть отражено непосредственно в алгоритме RLS. Здесь мы изучаем RLS алгоритм с точки зрения адаптивных фильтров, потому что (а) RLS алгоритм можно рассматривать как специальную версию адаптивного фильтра и (б) каждый параметр адаптивного фильтра имеет физическое значение. Компьютерное моделирование показывает, что этот алгоритм сходится в два раза быстрее обычного базового алгоритма. Это может играть важную роль в биотелеметрии, где снятие без помех ЭКГ сигнала для эффективного диагностирования и высокая скорость передачи данных необходимы, чтобы избежать дублирования импульсов и разрешения неопределенностей. Насколько нам известно, преобразование доменов не было рассмотрено ранее в контексте фильтрации помех сигналов ЭКГ. В этой статье мы представляем RLS алгоритм для удаления помех на ЭКГ. Этот алгоритм имеет меньшую вычислительную сложность и хорошие возможности фильтрации. Для изучения эффективности предложенного алгоритма эффективного удаления помех из сигнала ЭКГ, было проведено моделирование с помощью MIT-BIH базы данных для различных помех.


2. ПРИНЦИП: РЯД ФУРЬЕ
Любые периодические функции, удовлетворяющие условиям Дирихле, могут быть выражены в виде ряда масштабных величин синуса или косинуса с точки зрения частоты, с которой происходят колебания, кратные основной частоте.




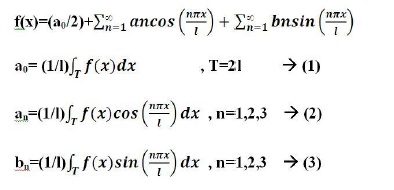
ЭКГ сигнал является периодическим, с частотой равной сердцебиению. Он также удовлетворяет условиям Дирихле:

  • Однозначность и конечность в заданном интервале;
  • Конечность числа минимумов и максимумов между конечными интервалами;
  • Конечное число разрывов первого рода.
  • Отсутствие разрывов второго рода
    • Следовательно, ряд Фурье может быть использован для представления ЭКГ сигнала.


    3. ВЫЧИСЛЕНИЯ:
    Как можно наблюдать на рисунке 1, один период ЭКГ сигнала представляет собой смесь треугольной и синусоидальной формы волны. Каждая существенная особенность ЭКГ сигнала может быть представлена сдвинутой и промасштабированной версией одной из таких осциллограмм, как показано ниже.

  • QRS, Q и S части ЭКГ сигнала могут быть представлены треугольной осциллограммой;
  • P, T и U части также могут быть представлены треугольной осциллограммой.
    • После того как мы создаем каждый из данных участков, они могут быть сложены для получения ЭКГ сигнала. Возьмем QRS составляющую как центральную и для остальных произведем сдвиг по отношению к этой части сигнала. Как создается периодическая QRS часть ЭКГ сигнала:



    Рис. 1. Осцилограмма QRS

    Из выражения (1), имеем:



    Генерация периодических p-волновых частей ЭКГ сигнала:



    Рис. 2. Осцилограмма p-волновой части сигнала


    4. ПОМЕХОПОДАВЛЕНИЕ
    Комбинированный с помехами сигнал подается на “основной вход” в компенсатор. Второй датчик получает помеху n1, которая не коррелирует с сигналом, но коррелировала некоторым неизвестным путем с помехой n0. Этот датчик обеспечивает "входное отношение" в компенсаторе. Помеха n1 фильтруется, чтобы вырабатывать вывод "у", который является близкой копией n0. Этот вывод вычитается из основного входа "s + n0" для создания системного выхода s+n0-y. Если известны характеристики каналов, по которым переданы помехи в первичные и вторичные датчики, можно создать фиксированный фильтр сравнения изменений n1 в у = n0. Выход фильтра затем может быть вычтен из основной входа, и выход системы будет содержать еденичный сигнал. Однако, поскольку, характеристики путей передачи считаются неизвестными или известны лишь приближенно, использование фиксированного фильтра не представляется возможным. Более того, даже если использование фиксированного фильтра было возможно, его характеристики должны быть скорректированы с трудно достижимой точностью, и малейшая ошибка может привести к усилению помехи. В системе, показанной на рис. 3, вторичный вход обрабатывается с помощью адаптивного фильтра, который автоматически настраивает свой импульсный отклик по методу наименьших квадратов. Такие алгоритмы как RLS реагируют на величину сигнала ошибки на выходе фильтра. В системах помехоподавления практическая цель заключается в создании системы выработки системного выхода s+n0-y, который лучше всего соответствует сигналу s, с учетом метода наименьших квадратов. Эта цель достигается путем подачи системного выхода обратно на адаптивный фильтр и настройки фильтра через адаптивный алгоритм для минимизации общей мощности системы. Другими словами, в системах адаптивного помехоподавления, системный выход используется как ошибка сигнала для адаптивного процесса.



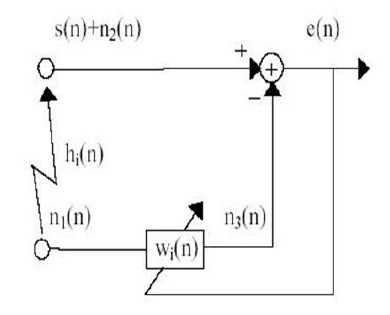
    Рис. 3. Адаптивный помехоподавитель

    5. RLS АЛГОРИТМ
    Целью работы алгоритма является выбор коэффициентов адаптивного фильтра таким образом, чтобы выходной сигнал у(k), в течение периода наблюдения, соответствовал полезному сигналу, насколько это возможно в смысле наименьших квадратов. Процесс минимизации требует доступной информации о входном сигнале в предыдущий момент времени. Кроме того, целевая функция, к которой мы стремимся минимизировать, является детерминированной. Общий FIR адаптивный фильтр реализован в прямой форме на рис. 3. Информация о входном сигнале в данный момент находится в векторе k.



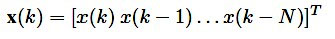
    обратная детерминированная корреляционная матрица может быть рассчитана в следующем виде:

    Полный RLS алгоритм описан в Алгоритме 5.1.

    Алгоритм 5.1


    6. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ
    Чтобы показать, что RLS алгоритм действительно эффективен в клинических ситуациях, этот метод был проверен с помощью нескольких записей ЭКГ с широким спектром волновых морфологии из MIT-BIH базы данных аритмии. В нашей работе мы использовали ЭКГ сигналы загрязненные помехами различной частоты, которые были оцифрованы в 200 выборок в секунду на каждый канал с 20 мВ в диапазоне. Тем не менее, реальные помехи могут быть получены из базы данных нормального синусового ритма (NSTDB).
    A. Адаптивная фильтрация помех от питания
    Помехи на линии электропередачи могут привести к серьезному повреждению биомедицинских записей. Мы предлагаем улучшенный адаптивный компенсатор для сокращения основной составляющей помехи линии электропередачи и гармоники в электрокардиограмме (ЭКГ). Метод отслеживает амплитуду, фазу и частоту всех помех для линии электропередачи для частот примерно до 4 Гц. Очищенный сигнал после применения всех методов сравнивается с первоначальным сигналом ЭКГ. Наш улучшенный адаптивный компенсатор показывает отношение к мощности зоны прямой помехи для основных компонентов до 30 дБ выше, чем при других методах. Кроме того, наш метод эффективен также для подавления гармоник помех линии электропередачи. Чтобы продемонстрировать мощностную помеху (PLI) мы выбрали моделирование синусоидальной волны частотой 50 Гц.


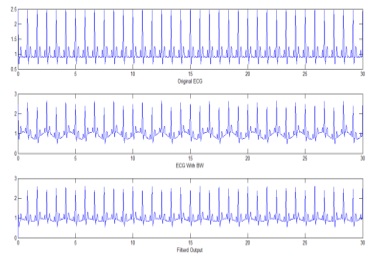
    B. Базовое блуждающее сокращение
    Загрязненный ЭКГ сигнал подан на главный вход адаптивного фильтра на рис. 3.



    Рис. 4. a) Чистый ЭКГ сигнал, b) ЭКГ с PLI помехой, c) Отфильтрованный по RLS алгоритму.


    Рис. 5. a) Чистый ЭКГ сигнал, b) ЭКГ с BW помехой, c) Отфильтрованный по RLS алгоритму.

    C. Адаптивная фильтрация мышечных помех.
    Чтобы показать эффективность фильтрации в присутствии нестационарных помех, мышечные помехи (MA) были взяты из MIT-BIH базы данных. Часто ЭКГ бывают загрязнены электрофизиологическими потенциалами, связанными с сокращением мышц человека. Такие мышечные артефакты усложняют интерпретацию ЭКГ или даже делают ее невозможной. Для удаления таких помех используются низкочастотные фильтры. Однако, частотный спектр мышечных помех может пересекаться с частотой сигналов мозга. Таким образом фильтры подавляют не только мышечные помехи, но и ценную информацию.


    Рис. 6. a) Чистый ЭКГ сигнал, b) ЭКГ с MA помехой, c) Отфильтрованный по RLS алгоритму

    D. Адаптивное снятие с электрода
    Для демонстрации этого мы используем чистый сигнал ЭКГ снятый с электродов, с добавлением EM помехи. EM помеха создается с частотой выше 15 Гц. Сигнал ЭКГ, загрязненный EM помехой, подается на вход адаптивного фильтра. EM помеха используется как опорный сигнал. На выходе фильтра получаем требуемое высокое разрешение сигнала ЭКГ. Результаты приведены на рис. 7.


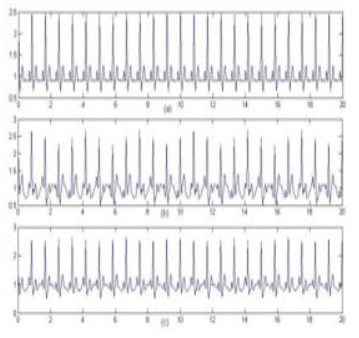
    Рис. 7. a) Чистый ЭКГ сигнал, b) ЭКГ с EM помехой, c) Отфильтрованный по RLS алгоритму.

    7. ЗАКЛЮЧЕНИЕ


    В данной работе представлен процесс удаления помех из ЭКГ сигнала основанный на использовании RLS адаптивного фильтра. Для этого, входной и полезный сигналы выбраны таким образом, что выходной фильтр выводит лучшую минимальную квадратную оценку исходного сигнала ЭКГ. Предложенный метод использует изменения в формуле обновления веса и, следовательно, приводит к росту скорости по отношению к соответствующим LMS основанным реализациям. В наших исследованиях, однако, подтверждено, что SNR предложенного алгоритма дает лучший результат. Кроме того, скорость сходимости быстрее, а также сложность вычислений меньше, чем для LMS реализаций. Результаты приведены в таблице 1.


    Типы помех Алгоритм SNR до фильтрации (в dbs) SNR после фильтрации (в dbs) SNR улучшение (в dbs)
    PLI RLS 17.81 26.94 9.13
    BW RLS 18.73 23.70 4.97
    MA RLS 18.73 22.77 4.04
    EM RLS 18.73 20.53 1.8

    Список литературы:

    1. [1] Paulo S.R. Denis, "Adaptive filtering Algorithms and Practical implementation”.
    2. [2] O. Sayadi and M. B. Shamsollahi, “Model-based fiducial points extraction for baseline wander electrocardiograms,” IEEE Trans. Biomed. Eng., vol.55, pp. 347-351, Jan.2008.
    3. [3] Y. Der Lin and Y. Hen Hu, “Power-line interference detection and suppression in ECG signal Processing,”. IEEE Trans. Biomed. Eng., vol.55, pp. 354-357, Jan.2008.
    4. [4] N. V. Thakor and Y.-S. Zhu,Applications of adaptive filtering to ECG analysis: noise cancellation and arrhythmia detection,”. IEEE Transactionson Biomedical Engineering, vol. 38, no. 8, pp. 785-794, 1991.
    5. [5] Farhang-Boroujeny, B., Adaptive Filters- Theory and Applications, John Wiley and Sons.Chichester,UK, 1998.
    6. [6] P. E.McSharry, G. D. Clifford, L. Tarassenko, and L. A. Smith, “A dynamical model for generating synthetic electrocardiogram signals,” IEEE Transactions on Biomedical Engineering, vol. 50, no.3, pp. 289- 294, 2003.