ЦИФРОВЫЕ ГЕНЕРАТОРНЫЕ ПРЕОБРАЗОВАТЕЛИ ПОВЫШЕННОЙ ЧУВСТВИТЕЛЬНОСТИ ДЛЯ СИСТЕМ УПРАВЛЕНИЯ И КОНТРОЛЯ
Авторы: ШАКУРСКИЙ В.К., ИВАНОВ В.В., НАГАЕВ Д.А.
Тольяттинский гос. университет
Источник: http://www.nbuv.gov.ua/portal/natural/tkea/texts/2008_1/13-15.pdf.
Рассматривается реализация режима сверхчувствительности в цифровых автоколебательных системах с целью синтеза цифровых генераторных преобразователей повышенной чувствительности.
Одной из проблем, решаемых исследователями и разработчиками генераторных преобразователей и модуляторов с выходным ЧМ- или ФМ-сигналом, является увеличение их чувствительности к управляющему параметру.
Частота генерируемого сигнала в основном определяется нулевой точкой эквивалентной фазочастотной характеристики (ФЧХ) разомкнутой цепи автоколебательной системы при условии выполнения баланса амплитуд. Во всех широко известных структурах квазигармонических автоколебательных систем чувствительность нулевой точки ФЧХ к управляющему параметру имеет потенциальные ограничения. Авторами [1] был выявлен новый эффект, позволяющий реализовать чувствительность, которая в десятки и сотни раз может превышать указанные потенциальные значения. Данный эффект был назван эффектом сверхчувствительности автоколебательных систем. Эффект реализуется введением в автоколебательную систему дополнительного фильтра с инвертированным наклоном ФЧХ по отношению к типичному наклону.
Эффект объясняется следующим. При вычитании двух типичных ФЧХ с близким друг к другу наклоном и смещенных относительно друг друга, нулевая точка эквивалентной ФЧХ может находиться далеко от области частот, ограниченной нулевыми точками вычитаемых ФЧХ. При сложении типичных ФЧХ нулевая точка эквивалентной ФЧХ всегда находится в области частот, ограниченной нулевыми точками суммируемых ФЧХ [1, с. 15].
Для инвертирования ФЧХ разработана двухканальная структура [1, с. 28]. Выполненные исследования показали, что эффект сверхчувствительности реализуется в любой автоколебательной системе указанного класса. Условием устойчивой работы автоколебательной системы в режиме сверхчувствительности является типичный наклон эквивалентной ФЧХ разомкнутой цепи [2, 3]. На базе указанного эффекта разработаны генераторные аналоговые параметрические преобразователи повышенной чувствительности с выходным ЧМ- и ФМ-сигналом, преобразователи девиации частоты и девиации фазы, модуляторы [1, 4].
Недостатком аналоговых преобразователей в режиме повышенной чувствительности является возрастание дополнительной погрешности при воздействии дестабилизирующих факторов. Избавиться от этого недостатка можно реализацией режима сверхчувствительности в цифровых автоколебательных системах. В цифровых генераторных преобразователях дополнительная погрешность равна нулю, но возникают другие проблемы, которые требуют проведения исследований. Это ступенчатость ФЧХ, проблема управления цифровой автоколебательной системой, проблема настройки заданной крутизны преобразования и другие.
Целью статьи является определение особенностей синтеза цифровых управляемых автоколебательных систем в режиме сверхчувствительности.
Рассмотрим реализацию цифровой автоколебательной системы с однопетлевой обратной связью в режиме сверхчувствительности, структура которой приведена на рис. 1. Система содержит полосный фильтр 1 с инвертированным наклоном ФЧХ, усилитель 2, нелинейный блок 3 и полосный фильтр 4 с типичной ФЧХ.
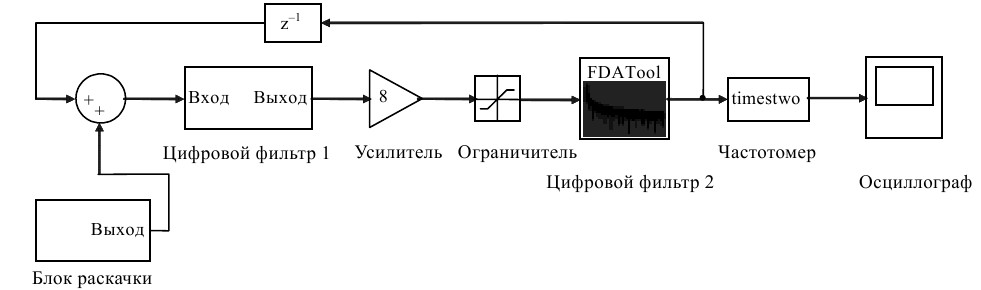
Исследования автоколебательной системы проводились в среде Simulink математической системы MATLAB. Была разработана модель цифровой автоколебательной системы, которая приведена на рис. 2.
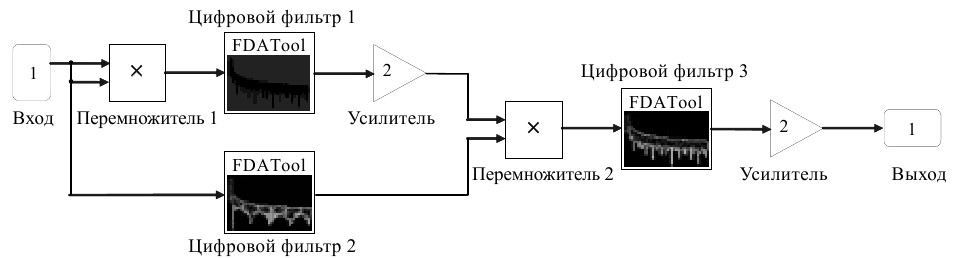
Модель фильтра с инвертированным наклоном ФЧХ приведена на рис. 3. Использовались цифровые полосные фильтры с конечной импульсной характеристикой (КИХ), т. к. они обладают линейными ФЧХ, что необходимо для получения линейных характеристик разрабатываемых преобразователей.
Наличие в модели фильтра с инвертированным наклоном ФЧХ смесителей приводит к жесткому возбуждению автоколебательной системы. Это потребовало введения блока раскачки (см. рис. 2). Для снятия характеристик используется частотомер и осциллограф. В обратную связь введен блок варьируемой задержки, с помощью которого имитируется управление частотой генерируемого сигнала изменением величины вносимого фазового сдвига.
Модель фильтра с инвертированным наклоном ФЧХ строится по двухканальной схеме. Второй канал работает на удвоенной частоте входного сигнала. Для этого используется перемножитель 1. С помощью перемножителя 2 и фильтра 3 выделяется сигнал с основной частотой. Если фазовый сдвиг в фильтре 2 больше, чем суммарный фазовый сдвиг в фильтрах 1 и 3, то результирующий фазовый сдвиг в данной модели фильтра меняет знак по сравнению с типичным фильтром. Вариацией наклонов ФЧХ фильтров 1, 2 и 3 можно получить эквивалентную ФЧХ с типичным наклоном, с нулевым наклоном и с инвертированным наклоном.
О пределим возможные частоты генерируемых колебаний. Уравнение баланса фаз для структуры автоколебательной системы рис. 2 имеет вид

Используем выражение для ФЧХ цифрового КИХ-фильтра
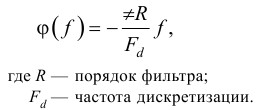
Запишем также выражение для ФЧХ блока задержки
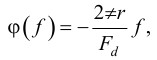
где r — количество интервалов между выборками, на время которых происходит задержка (r?1). Подставим их в (1) и получим выражение для частоты генерируемых сигналов:
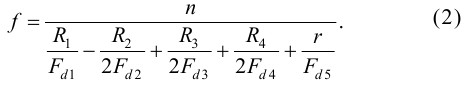
Условием устойчивости колебаний является положительный знак знаменателя (2). Для увеличения чувствительности необходимо минимизировать знаменатель.
Выполненные исследования компьютерной цифровой модели показали, что порядок фильтров (количество выборок КИХ) и частоту дискретизации следует использовать для настройки автоколебательной системы. При этом полоса фильтра определяется отношением частоты дискретизации к порядку фильтра. С учетом ступенчатого характера ФЧХ уве- личение разрешающей способности в полосе фильтра требует увеличения частоты дискретизации и соответствующего увеличения порядка фильтров.
Наиболее эффективным способом управления частотой генерируемого сигнала является внесение в цепь обратной связи автоколебательной системы варьируемого частотонезависимого фазового сдвига. Управляющий фазовращатель может быть вне процессора, реализующего автоколебательную систему.
Вводя в уравнение баланса фаз управляемый фазовый сдвиг фазовращателя ±?(x), получим выражение для характеристики преобразования фазового сдвига в частоту генерируемого сигнала:
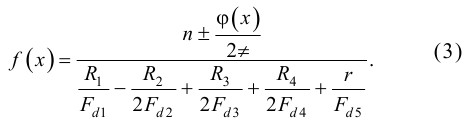
Выполненные эксперименты на компьютерных моделях подтверждают сделанные выводы. Например, при крутизне эквивалентной ФЧХ фильтра 1 (рис. 1) S?1 = ?·6,75·10 –3 и крутизне эквивалентной ФЧХ фильтра 4 S?2 = ?·9·10 –3 получена характеристика, приведенная на рис. 4, где фазовый сдвиг — в градусах, а частота — в герцах.
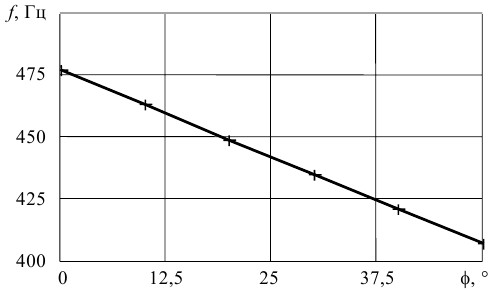
Характеристика получена варьированием вносимой задержки, величина которой затем пересчитывалась в фазовый сдвиг на частоте генерируемого сигнала. Характеристика имеет ступенчатый характер (на рис. 4 она аппроксимирована линией).
Выполнены аналогичные исследования других цифровых автоколебательных систем в режиме повышенной чувствительности, например с двухпетлевой обратной связью, с комбинационным взаимодействием трех сигналов некратных частот [5, 6].
По результатам исследований можно сделать следующие выводы.
Линейные ФЧХ цифровых фильтров проходят через начало координат, поэтому смещение нулевых точек ФЧХ приводит к одновременному изменению их крутизны и наоборот. Это усложняет процедуру настройки цифровых генераторных преобразователей.
Ступенчатость ФЧХ цифровых фильтров приводит к дискретности характеристики преобразователя. Увеличение чувствительности преобразователя требует увеличения разрешающей способности и должно сопровождаться увеличением порядка фильтров и увеличением частоты дискретизации. Возрастает объем операций на каждом интервале между выборками. В свою очередь это снижает быстродействие и ограничивает диапазон частот генерируемых сигналов.
В структуре цифровой автоколебательной системы в цепи обратной связи необходим элемент задержки как минимум на один интервал между выборками. Это обеспечивает устойчивость автоколебаний.
Наклон эквивалентной ФЧХ автоколебательной системы должен быть типичным. В противном случае возникает эффект частотной неустойчивости. В процессе возбуждения автоколебаний происходит смещение частоты в сторону границы полосы фильтра. Нарушается баланс амплитуд и происходит срыв автоколебаний.
Полученные результаты позволяют говорить о перспективности данного нового класса цифровых генераторных преобразователей.
Список литературы:
- Иванов В. В., Шакурский В. К. Генераторные, фазовые и частотные преобразователи и модуляторы.— М.: Радио и связь, 2003.;
- Иванов В. В., Шакурский В. К. Эффект преобразования в комбинационном генераторе девиации частоты сигнала синхро- низации // Радиотехника.— 2004.— № 4.— С. 37—40.;
- Иванов В. В., Шакурский В. К. Анализ свойств управляе- мого генератора в режиме повышенной чувствительности // Элек- тросвязь.— 2004.— № 7.— С. 43—51.;
- Иванов В. В., Шакурский В. К. Увеличение чувствитель- ности генераторных параметрических преобразователей // Изв. вузов. Приборостроение.— 2005.— № 7.— С. 47—51.;
- Иванов В. В. Частотно-фазовые преобразователи повышен- ной чувствительности // Изв. вузов. Приборостроение.— 2005.— № 9.— С. 13—17.
- Иванов В. В., Нагаев Д. А. Цифровые генераторные пре- образователи сигналов с угловой модуляцией // Изв. Самарского научного центра РАН.— 2006.— Спец. выпуск.— С. 31—34.