Источник: Прохоров В.Г. Использование сверточных нейронных сетей для распознавания рукописных символов // УкрПрог, Киев, Украина. 2008.
УДК 004.934
ИСПОЛЬЗОВАНИЕ СВЕРТОЧНЫХ СЕТЕЙ ДЛЯ РАСПОЗНАВАНИЯ
РУКОПИСНЫХ СИМВОЛОВ
В. Г. Прохоров
Институт программных систем НАН Украины.
03187, Киев-187, проспект Академика Глушкова, 40.
E-mail: makumazan84@yahoo.com
Рассмотрены особенности классического метода распознавания символов с помощью нейронных сетей. Предложен алгоритм распознавания символов, использующий сети свертки, отмечен ряд особенностей данного подхода. Приведены экспериментальные данные, иллюстрирующие эффективность предложенного алгоритма.
Features of classical recognition using neural network were
reviewed. A new approach, which uses convolutional networks, was given along
with its characteristics. An experimental data, illustrating the proposed
algorithm’s efficiency was given.
Введение
Способность многослойных нейронных сетей, обученных методом градиентного спуска к построению сложных многомерных областей на основе большого числа обучающих примеров, позволяет применять их в качестве классификатора для распознавания образов. Несмотря на это, в традиционной полносвязной нейронной сети есть ряд недостатков, понижающих эффективность их работы.
Прежде всего, это большой размер изображений (под изображением понимается графическое представление распознаваемого образа, представленное в виде набора пикселов), который может достигать нескольких сотен. Для корректного обучения таким данным требуется увеличить число скрытых нейронов, что приводит к увеличению числа параметров, и, как следствие, понижает скорость обучения, требует большую обучающую выборку. Но самым большим ограничением таких сетей является то, что они не отличаются инвариантностью к различным деформациям, например, переносу или незначительному искажению входного сигнала. Следует заметить, что вариации написания символов содержат такие деформации (одной из них можно считать индивидуальный почерк, который существенно меняет написание символа). В принципе, эту проблему можно решить за счет пополнения обучающей выборки примерами таких искаженных символов, однако это приведет к низкой скорости обучения и, что хуже, может привести к плохой обобщающей способности сети [1].
Еще одним недостатком классических полносвязных сетей является то, что они игнорируют топологию входного изображения. Пиксели можно подавать на вход в любом фиксированном порядке, и это не повлияет на исход обучения. С другой стороны, изображения имеют четкую двухмерную структуру: соседние пиксели связаны между собой, и эта структура несет в себе ценную информацию об изображении. Локальная связь пикселов – основная причина использования определенных механизмов извлечения локальных признаков на определенной области изображения с последующим формированием некой системы таких признаков. Такая система является интуитивно понятной: различные конфигурации соседних пикселов формируют определенные категории (углы, края, и т.д.). Очевидно, что эффективная система распознавания образов должна основываться на алгоритме, учитывающем такие особенности входных данных.
В настоящей работе рассмотрены сверточные сети – один из подвидов нейронных сетей, который в значительной мере устраняет вышеописанные недостатки полносвязных нейронных сетей и гарантирует быстрое обучение и распознавание образов. Далее будет подробно рассмотрена архитектура такой сети, особенности ее слоев и принцип действия.
1. Общие свойства и особенности функционирования сверточных сетей. Описание типичной сверточной сети
В основе сверточных сетей лежат три
механизма, используемые для достижения инвариантности к переносу,
масштабированию, незначительным искажениям:
Локальное извлечение
признаков. Каждый нейрон получает входной сигнал от локального рецептивного
поля в предыдущем слое, извлекая, таким образом, его локальные признаки. Как
только признак извлечен – его точное расположение уже не имеет значение,
поскольку установлено его местонахождение относительно других признаков.
Формирование слоев в виде набора карт признаков. Каждый вычислительный слой состоит из множества карт-признаков – плоскостей, на которых все нейроны должны использовать одно и то же множество синаптических весов. Такая форма усложняет структуру сети, однако имеет два важных преимущества: инвариантность к смещению, которое достигается с помощью свертки с ядром небольшого размера, и сокращение числа свободных параметров, которое достигается за счет совместного использования синаптических весов нейронами одной и той же карты.
Подвыборка. За каждым слоем свертки следует вычислительный слой, осуществляющий локальное усреднение и подвыборку. За счет этого, достигается уменьшение разрешения для карт признаков. Такая операция приводит к понижению чувствительности выходного сигнала оператора отображения признаков к незначительному смещению и прочим формам деформации. В качестве такого оператора выступает одна из сигмоидальных функций, используемых при построении нейронных сетей, например гиперболический тангенс.
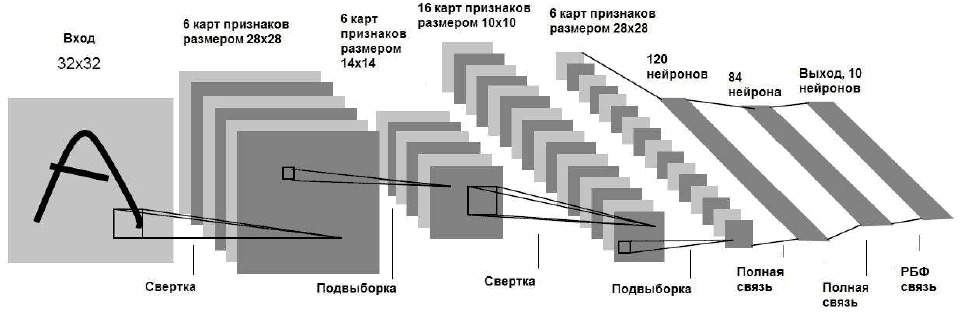
Следует заметить, что последовательное применение свертки и подвыборки приводит к так назывемому повышению уровня признаков: если первый слой извлекает локальные признаки, из областей изображения, то последующие слои извлекают общие признаки, которые также называются признаками высокого порядка. На рисунке показана сеть свертки, реализующая распознавание изображений. Рассмотрим особенности ее функционирования.

Рисунок
Во входной слой поступает центрированное изображение символа. Такая операция делается для того, чтобы характерные признаки рисунка (дуги, концевые точки) находились в центре рецептивного поля при извлечении признаков высокого порядка. В вышеописанной сети, стандартные символы базы MNIST размером 28х28 пикселов позиционировались в центр изображения 32х32 пикселя. Значения входных пикселов затем нормализируется для ускорения сходимости обучения. Точные нормализированные значения пикселов вычисляется в зависимости от типа используемой активационной функции, в данном случае фоновому пикселю соответствует значение –0.1, а формирующему символ – 1.175.[2]
Первый скрытый слой является слоем свертки. Он состоит из 6 карт признаков размером 28х28. Рассмотрим процесс формирования этого слоя, поскольку остальные сверточные слои формируются подобным образом. Каждый элемент карты признаков соединен с областью размером 5х5 на входном изображении. Следственно, каждый элемент карты имеет 25 обучаемых коэффициентов и обучаемый сдвиг. Значение элемента карты вычисляется по формуле
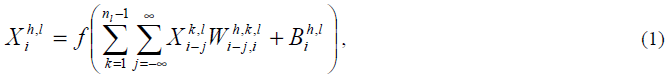
где Xih,l – значение элемента i в карте признаков h слоя l, nl – количество карт признаков в слое l, Bih,l – значение сдвига для элемента i в карте признаков h слоя l, W - синаптический вес связи между элементом i в карте признаков h слоя l и элементом i-j карты k слоя l-1.
Рецептивные поля соседних элементов на карте признаков соединены с соседними областями предыдущего слоя, следственно эти поля частично накладываются друг на друга. Как было сказано ранее, все элементы карты признаков имеют общий набор из 25 весов и сдвига, поэтому можно сказать, что они извлекают один и тот же признак во всевозможных областях предыдущего слоя. В данном случае, 6 различных карт второго слоя извлекают 6 различных признаков для разных областей изображения. Значения всех элементов карты признаков вычисляются путем последовательного прохода по входному слою и применению формулы (1) к тем, областям, которые являются локальными рецептивными для данных элементов карты признаков. Интересной особенностью сверточных слоев является тот факт, что при сдвиге входного изображения значения карт признаков будут сдвинуты на ту же самую величину. За счет этого сверточные сети обладают инвариантностью к сдвигам и искажениям входного сигнала [3].
Итак, первый скрытый слой является слоем свертки, который содержит 6 карт признаков размером 28х28. Каждый его элемент соединен с областью размером 5х5 на входном изображении. Первый скрытый слой содержит 122,304 связей и 156 обучаемых параметров. Такая экономия памяти и, что главное, вычислительных затрат достигается за счет совместного использования весов элементами одной карты.
Второй скрытый слой является слоем подвыборки. Он состоит из 6 карт признаков размером 14х14, причем каждый из элементов карт этого слоя соединен с областью 2х2 в соответствующей карте признаков предыдущего слоя. Значения элементов слоев свертки также вычисляются по формуле (1). Важно понимать, что рецептивные поля для элементов слоя подвыборки не перекрываются, следственно карты признаков этого слоя содержат в 2 раза меньше строк и столбцов, чем в предыдущем слое. Стоит заметить, что поскольку задачей данного слоя является подвыборка (т.е. локальное усреднение), не обязательно хранить для карт 4 веса и сдвиг, а достаточно обойтись одним общим весом и сдвигом [4]. Таким образом, второй скрытый слой содержит 5,880 связей и 12 обучаемых параметров.
Третий скрытый слой является сверточным слоем с 16 картами признаков размером 10х10. Каждый элемент в каждой карте признаков связан с несколькими областями размером 5х5 определенных карт предыдущего слоя. Такому необычному способу связи этих двух слоев есть ряд объяснений. Во-первых, соединение всех карт второго слоя со всеми картами третьего слоя значительно увеличило бы количество связей. Соединение карт «одна к одной» (при условии, что в третьем слое всего 6 карт) не дало бы каких либо результатов – это стало бы еще одним повторением свертки, которое уже присутствовало между первым и вторым слоями [5]. С другой стороны, соединение карт третьего слоя с определенными картами второго слоя нарушает симметрию сети, и заставляет ее извлекать совсем другие признаки, которые будут дополнять ранее извлеченные [6]. Как правило, архитектор сети сам принимает решение о том, по какому принципу организовывать соединение карт второго и третьего слоев. Связь карт, используемая при проектировании данной сети, приведена в таб. 1.
Таблица 1. Параметры соединения третьего и четвертого слоев

Рассмотрим принцип формирования связей в таб. 1. Первые 6 карт третьего слоя соединены с наборами из трех последовательных карт второго слоя. Следующие 6 карт связаны с наборами 4 последовательных карт. Карты 13–15 третьего слоя связаны с непоследовательными наборами из 4 карт. И последняя карта третьего слоя связана со всеми картами предыдущего слоя. В общем, третий слой содержит 151,600 связей и 1,516 обучаемых параметров.
Четвертый слой реализует подвыборку и состоит из 16 карт признаков размером 5х5. Этот слой мало чем отличается от второго подвыборочного слоя: каждый его элемент связан с областью 2х2 на соответствующей карте предыдущего слоя. Четвертый скрытый слой содержит 2,000 соединений и 32 обучаемых параметра. Пятый скрытый слой являет полносвязным сверточным слоем и содержит 120 элементов. Каждый из них соединен 5х5 областями со всеми 16 картами четвертого слоя. В этом смысле он является гибридом сверточного и полносвязного слоев – поскольку размер его карт равен 1х1, он может принимать сигнал рецепторного поля размером 5х5 и при этом, он связан со всеми картами предыдущего слоя. Пятый слой содержит 48,120 обучаемых параметров.
Шестой слой содержит 84 элемента-нейрона и также является полносвязным. Он содержит 10,164 обучаемых параметров. Перед тем, как перейти к описанию седьмого, последнего слоя, стоит рассмотреть особенности формирования сигнала и активирующей функции, используемой в вышеупомянутых слоях сверточной сети. Как и в случае с классическими нейронными сетями, на вход каждого элемента сети поступает взвешенная сумма – скалярное произведение между входным вектором сигналов и весовым вектором, который затем подается в качестве аргумента активирующей функции. В данном случае, такой функцией является гиперболический тангенс:
![]()
где, f (a) – искомое значение элемента, a – взвешенная сумма сигналов предыдущего слоя, A, S – параметры активирующей функции.
Такая активирующая функция является нечетной, с горизонтальными асимптотами +A и –A, а параметр S определяет наклон функции в начале координат. В данном случае, в качестве параметров брались значения A = 1.7159 и S = 2/3. Такие значения параметров были выбраны не случайно – при них активирующая функция обладает рядом полезных свойств [7].
![]()
В начале координат тангенс угла наклона близок к единице.
Вторая производная достигает максимума при a = 1. В отличии от первых шести слоев, последний слой формирует сигнал с помощью так называемых Радиально Базисной Функции (РБФ) для каждого из классов, используя 84 входных сигнала предыдущего уровня:

где xj
– значение сигнала j-того
элемента предыдущего слоя, wij
– значение весового коэффициента для связи данных элементов.
Другими словами, РБФ вычисляет
Евклидово расстояние между входным и весовым векторами. Чем больше отличаются
эти векторы – тем больше значение функции. Такая сущность РБФ функции крайне
полезна для последнего слоя нейросети: фактически, она показывает насколько
отличаются входной вектор и эталонный вектор данного класса. В этом случае
функция потерь должна быть настроена таким образом, чтоб выходной вектор шестого
слоя был максимально приближен к параметрическому вектору, описывающему эталон
данного класса.
Следует заметить, что в контексте данной задачи (распознавание рукописных цифр), использование РБФ функций не является оптимальным решением. Действительно, использование сигмоида (как и в предыдущих слоях) вместе с классическим эталонным вектором вида «1 из N» проще в программной реализации и требует меньших вычислительных ресурсов. Однако такое решение не является оптимальным при расширении задачи, например, распознавании не только цифр (10 эталонных классов), но и букв алфавита (больших и малых), знаков пунктуации, и так далее. В этом случае число возможных классов равно нескольким десяткам. При использовании эталонных векторов вида «1 из N» для распознавания объектов, принадлежащих к большому количеству классов, у сети резко падает эффективность. Это связано, прежде всего, с малой чувствительностью сигмоида к распознаванию многих классов и приводит к медленному обучению и низкой точности распознавания. Особенно осложняет распознавание наличие похожих символов: «О» и «0», «l» и «1», а также больших и малых букв [8]. Таким образом, использование РБФ функций является необходимым условием для адаптации сверточной сети к решению новых задач, подразумевающих наличие большого числа различных классов образов.
Кратко рассмотрим этап обратного прохода при обучении. По своей сути, он не отличается от прохода по классической нейронной сети, но при реализации необходимо учитывать особенности архитектуры сверточной сети – совместного использования весов нейронами одной карты признаков. Для оптимизации сходимости сверточных сетей можно использовать стандартные механизмы оптимизации нейронных сетей: пакетное обучение, использование матрицы Гессе, пропуск обратного хода в случае малой ошибки и другие. На практике, лучшая способность сети к обобщению достигается пополнением обучающей выборки деформированными примерами, а также изъятием чрезмерно искаженных примеров, на изучение которых сеть тратит много времени.
2. Экспериментальная оценка эффективности работы сверточной сети. Сравнение с аналогичными алгоритмами
Для оценки
эффективности предложенного подхода разработана программа Cunning Eye
Convolutional, реализующая распознавание символов с помощью сверточной сети, а
также программа Cunning Eye Neuro, использующая классическую полносвязную
нейросеть. Поскольку целью данного эксперимента являлась оценка эффективности
работы различных нейросетей, в сравнении не участвовали другие методы
распознавания (линейные классификаторы, SVN машины и пр.), принадлежащие к
принципиально другим
семействам алгоритмов распознавания.
Обе системы распознавания обучались на одной и той же выборке, а затем тестировались на единой для всех проверочной выборке. В качестве таких выборок были взяты обучающая и проверочная базы рукописных символов MNIST. Данная база является общепринятым эталоном для оценки эффективности алгоритмов распознавания цифр и используется учеными, и энтузиастами со всего мира. Размер обучающей выборки – 60,000 символов, размер проверочной – 10,000 символов. Исходный размер образов в базе – 28х28 пикселов. Во всех случаях, графические образы цифр не проходили предварительную обработку (центрирование, фильтрация, масштабирование).
В качестве основных параметров оценки работы системы оценивались такие
характеристики:
– скорость обучения;
– точность распознавания символов из обучающей выборки;
– точность распознавания символов из тестировочной выборки.
Кратко рассмотрим используемые в экспериментах системы распознавания символов. Cunning Eye Convolutional. Данная система реализует распознавание цифр с помощью сверточной сети, показанной на рисунке. Для подачи на вход графические образы из базы позиционировались в центр изображения 32х32 пикселя. Cunning Eye Neuro. Данная система проводит распознавание символов с помощью классических трехслойных нейросетей с архитектурами 784-50-10, 196-50-10, 361-50-10. В первом случае, цифры с разрешением 28х28 пикселей без изменений поступают на вход нейросети. В остальных случаях цифры масштабировались и приводились к размерам 14х14 и 19х19 пикселей. Количество нейронов скрытого слоя было определено методом проб и ошибок. Проанализируем результаты экспериментов, записанные в таб. 2. Необходимо отметить, что обе системы не смогли запомнить некоторое число символов. В этих случаях в качестве времени обучения бралось время, за которое система обучалась распознаванию максимального числа символов.
Таблица 2. Результаты экспериментов

Что касается
непосредственных результатов эксперимента, то стоит отметить малую эффективность
классических нейронных сетей по сравнению со сверточными сетями.
Превосходство последних видно при сравнении обобщающих
способностей классической и сверточной сетей. Как видно из таб. 2, классическая
нейросеть способна эффективно обучаться значительному числу образов,
однако плохая способность к обобщению приводит к плохим
результатам распознавания неизвестных системе символов из обучающей
выборки. Таким образом, можно констатировать большую эффективность сверточной
сети при распознавании рукописных цифр.
3. Параллельный алгоритм обучения сверточных сетей
Единственным недостатком сверточных сетей является их низкая, по сравнению с классическими алгоритмами, скорость обучения. Тем не менее, архитектура сверточных сетей позволяет значительно уменьшить время обучения. Поскольку первые 4 слоя не являются полносвязными, эта часть сети легко поддается распараллеливанию, и, как результат – уменьшению времени обучения. На данный момент лидирующие производители центральных процессоров предлагают различные многоядерные решения, которые позволяют значительно ускорить обучение сверточной сети [9].
Существует несколько способов распараллеливания нейросетевых алгоритмов обучения: распараллеливание действий над первыми 4 слоями, распределение в разные потоки прямого и обратного хода, и др. Выбор одного из них для последующего использования при обучении, определяется особенностями сети, и, что особенно важно, особенностями архитектуры компьютера. Стоит заметить, что распараллеливание нейросетевых алгоритмов имеет смысл при использовании 2 или больше физических процессоров, установленных на компьютере.
Рассмотрим распараллеливание нейронной сверточной сети с использованием двуядерного процессора. Вначале, необходимо создать два потока, каждый из которых берет пример из обучающей выборки и выполняют прямой проход для этих примеров. На данном этапе, появляется проблема хранения значений сигналов нейронов, так как эти сигналы используются на этапе обратного прохода. Такая проблема решается хранением значений нейронов для каждого примера. Независимое хранение сигналов позволяет разным потокам не перезаписывать общие промежуточные данные.
Еще одной трудностью распараллеливания при обратном проходе может стать обеспечение корректного изменения весов, т.е. непосредственно обучения сети. Действительно, в случае совместного изменения значений связей несколькими потоками, существует теоретическая угроза того, что сеть будет сходится медленно, поскольку изменения связей проводятся для двух разных примеров. Существует несколько вариантов решения этой проблемы, например вычисление градиента для изменения значений весов между эпохами. Однако, наиболее эффективным решением является уменьшение скорости обучения.
Для иллюстрации правильности последнего утверждения рассмотрим самый нежелательный вариант при изменении весов. Пусть, для определенного выходного сигнала сети, значение, соответствующие двум разным примерам равны 1 и –1 соответственно (данные значения являются максимальным и минимальным значениями активационной функции). В этом случае, ошибка для данного нейрона равна 2. Проследим обратное распространение этой ошибки. При распределении этой ошибки по различным связям, ведущих из предпоследнего в последний слой, проводится умножение суммарной ошибки на производную активирующей функции. Поскольку максимальное значение производной равно 1, ошибка все еще равна 2 (на этом этапе такую ошибку называют частной, поскольку она представляет собой погрешность определенного сигнала). При изменении значения веса коррекция определяется как произведение частной ошибки на скорость обучения. При малых значениях скорости обучения, например, 0.001, общая погрешность коррекции равна 0.002, т.е. в самом плохом случае погрешность составляет 0.2 % (для выходного сигнала, с максимальным значением 1). Такая погрешность коррекции относительно мала, и не может сильно влиять на сходимость сети. С другой стороны, время, выигранное на распараллеливании алгоритма, позволяет провести больше итераций и компенсировать ошибки обучения, вызванные незначительные погрешности коррекции.
В работе [9] приводятся результаты распараллеленного обучения сверточной сети на компьютере с процессором AMD Athlon X2 4400+. Скорость обработки примеров выросла со 12 до 23 примеров в секунду, что соответствует приросту скорости на 92 % (низкая скорость обработки примеров объясняется ее измененной структурой и особенностями реализации). Стоит заметить, что вышеописанный параллельный алгоритм не учитывает неполносвязность первых слоев сверточной сети, а следственно может быть оптимизирован.
Выводы
Еще одним преимуществом сверточных сетей является их универсальность в задачах распознавания: этот подвид нейронных сетей можно использовать для распознавания лиц, проектирования систем компьютерного зрения. Как показано в [10], применение сверточных сетей вместе с классификатором Витерби позволяет достаточно распознавать отдельные рукописные слова. Подвид сверточных сетей, так называемые TDNN сети (Time Delay Neural Networks) применяется при распознавании речи. В этом случае, операции свертки и подвыборки выявляют определенные значения сигналов, а карты признаков хранят привязаны к временной составляющей сигнала и их нейроны также совместно используют веса.
Подводя итог, стоит упомянуть, что сверточные сети являются наилучшим алгоритмом распознавания символов с искажениями, например так называемых CAPTCHA тестов. Распознавание таких изображений является серьезной задачей, которую неспособны эффективно решать нейронные сети других видов. Для решения такой задачи необходимо использовать многомодульную систему распознавания, которая использует сверточные сети, классификатор Витерби и графотрансформирующую сеть для определения отдельных символов на изображении.
1. Le Cunn Y., Bottou L., Orr G. B. “Neural Networks: Tricks of the trade”,
Springer . – 1998. – Р. 1 – 5.
2. Форсайт Д., Понс Д. “Компьютерное зрение. Современный подход.”– М.: Вильямс,
2004. – С. 603 – 610.
3. Burges C.J.C. “A Method for Training Neural Network to Recognize Character
Strings”, AT&T Bell Laboratories. – 1992. – Р. 1 – 8.
4. Simard P.Y. “Best Practices for Convolutional Neural Networks Applied to
Visual Document Analysis”, Microsoft . – 1998. – Р. 23 – 24.
5. Simard P.Y. “Transformation Invariance in Pattern Recognition”, Speech and
Image Processing Services Research AT&T Lab. – 1998. – Р.
23 – 24.
6. Vaillant R. “Localization of Objects in Images”, Speech and Image Processing
Services Research AT&T Lab. – 1994. – Р. 1 – 13.
7. Хайкин C. «Нейронные сети. Полный курс» Изд. второе (исправленное). Прэнтис
Холл. – 2006. – С. 239 – 298 ; 308 – 315.
8. Le Cunn Y., Bottou L., Haffner P. “Gradient Based Learning Applied to
Document Recognition”, IEEE Press. – 1998 – Р. 4 – 12.
9. O’Neal M. “Neural Networks for recognition of Handwritten Digits”, 2006. – Р
.1.
http://www.codeproject.com/KB/library/NeuralNetRecognition.aspx .
10. Le Cunn Y., Bottou L., Bengio Y. “Reading checks with multilayer graph
transforming networks”, Speech and Image Processing Services Research
AT&T Lab. – 1997. – Р. 1 – 4.