ОБЩАЯ НЕЭФФЕКТИВНОСТЬ ИСПОЛЬЗОВАНИЯ СУММАРНОГО ГРАДИЕНТА ВЫБОРКИ ПРИ ОБУЧЕНИИ НЕЙРОННОЙ СЕТИ
Царегородцев В.Г.
www.NeuroPro.ru tsar@neuropro.ru
На наборе сложных реальных задач обучения
нейросети-классификатора сравнивается эффективность теоретических методов
оптимизации(наискорейший спуск по суммарному градиенту выборки, метод
сопряженных градиентов, одномерная оптимизация шага вдоль направления спуска) со
стохастическими методами обучением с постоянным шагом и/или коррекцией нейросети
после просмотра очередного примера обучающей выборки. Подтверждается
преимущество и потенциальные возможности стохастических методов.
1. Введение
В качестве одной из нейросетевых парадигм, используемых при решении задач регрессии и классификации с учителем, широко применяются нейронные сети, обучаемые методом обратного распространения ошибки [1], эффективно и параллельно вычисляющим вектор градиента целевой функции по адаптивным параметрам сети. Коррекция адаптивных параметров нейросети вдоль направления антиградиента называется обучением. При этом используется обучающая выборка из набора векторов входных воздействий, и сопоставленных с ними векторов требуемых откликов нейросети. Возможность быстрого вычисления градиента позволяет применить весь спектр методов градиентной оптимизации для ускорения обучения сети. Предполагая, что упорядочение алгоритмов оптимизации по эффективности сохранится и при применении их для обучения нейросетей, обычно алгоритмы оптимизации упорядочивают следующим образом по нарастанию сложности реализации и предположительному росту скорости обучения-оптимизации [2]:
коррекция сети после просмотра очередного примера выборки по антиградиенту текущего примера (попримерное обучение нейросети, т.н. online-обучение);
накопление суммарного градиента по примерам выборки и шаг в сторону минимизации суммарного критерия качества суммы невязок отдельных примеров (обучение по суммарному градиенту, т.н. batch-обучение);
адаптация шага вдоль суммарного антиградиента (в общем случае одномерная оптимизация величины шага вдоль направления спуска: использование динамически изменяющегося шага вместо обучения с постоянным шагом в п.1-2;
надстроенные над суммарным градиентом метод сопряженных градиентов или квазиньютоновские методы с ограниченной памятью и оптимизацией шага, либо свободные от оптимизации шага псевдоньютоновские методы [3].
Обзор этих методов применительно к нейронным сетям дан, например, в [2,4]. Однако, недавние работы [5,6] показывают неэффективность batch-обучения по сравнению с online-обучением при неадаптивном шаге коррекции и достаточно больших обучающих выборках. Статья [6] описывает и критикует многие мифы, связанные с batch-обучением как более "теоретическим" по своей природе и являющимся базой для применения быстрых антиовражных алгоритмов оптимизации, поскольку часто на практике "?on large problems, a carefully tuned online algorithm outperforms most accelerated or second-order batch techniques, including conjugate gradient" [7, с.157] т.е. на сложных задачах online-обучение превосходит по методы batch-обучения, включая такие эффективные реализации последних, как метод сопряженных градиентов. В [5,6] рассмотрен именно случай сложных реальных практических задач, а многие ранее описанные неудачи базовых методов объясняются неоптимальными настройками этих алгоритмов, например, слишком консервативным выбором шага. Настоящая работа проверяет выводы [5,6] при обучающих выборках в среднем бóльшего, по сравнению со взятыми в [6], размера, и сравнивает более широкий круг методов обучения. Так, несмотря на процитированное выше замечание из [7], нет публикаций со сравнением именно предельных случаев online-обучения с постоянным шагом с одной стороны и хорошего антиовражного метода оптимизации (метода сопряженных градиентов или квазиньютоновского с ограниченной памятью), использующего при этом одномерную оптимизацию вдоль направления спуска, с другой стороны. Здесь этот пробел восполняется. Результаты экспериментов говорят, что затраты на одномерную оптимизацию шага не дают практической пользы, обучение по суммарному градиенту (с оптимизацией шага или без неё) всегда проигрывает online-обучению, online-обучение часто обгоняет метод сопряженных градиентов.
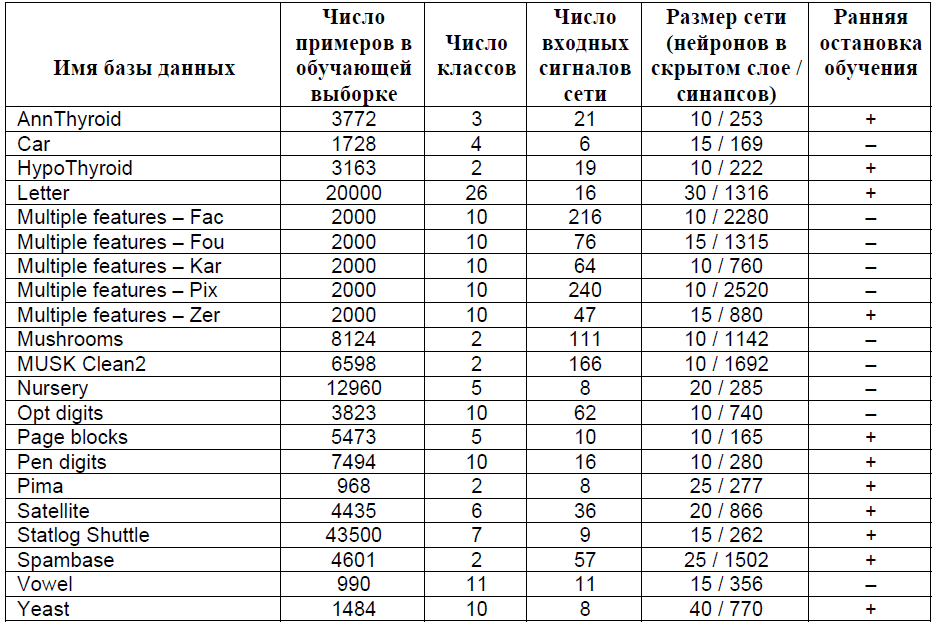
Таблица 1. Свойства задач (баз данных) и размеры нейронных сетей для них.

2. Задачи и базы данных, использованные в экспериментах
Взята 21 база реальных данных из UCI KDD Database Repository (http://kdd.ics.uci.edu/), во всех случая решается задача классификации с учителем. Свойства баз данных (число примеров, входов сети, число классов), размер нейросетей в виде числа нейронов в скрытом слое указаны в Таблице 1. Остановка обучения при достижении правильного решения заданного числа примеров применяется для случаев, когда присутствуют противоречивые данные или безошибочное обучение возможно только после значительного увеличения размера нейросети. Дополнительные независимые тестовые выборки имеются только у пяти задач, поэтому в работе не анализируется влияние алгоритмов обучения на обобщающие способности обученных сетей из-за невозможности показать стабильность отдельных замеченных эффектов.
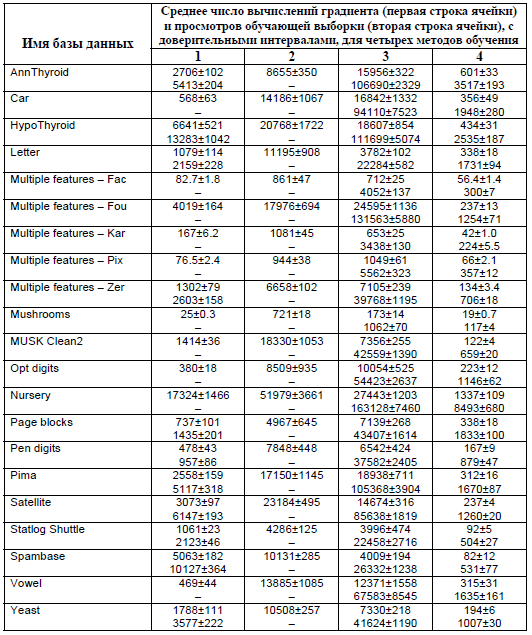
Таблица 2. Скорости разных методов обучения.
3. Результаты экспериментов: скорость обучения
Сравниваются между собой 4 следующих метода, соответствующие приведенной ранее во Введении иерархии:
Метод попримерной коррекции (online-обучение) с предварительно задаваемым неадаптивным шагом.
Метод спуска по суммарному антиградиенту (batch-обучение) с предварительно задаваемым неадаптивным шагом.
Метод наискорейшего спуска по суммарному антиградиенту (batch-обучение) с адаптацией шага на каждой итерации методом квадратичной аппроксимации. Процедура оптимизации шага использует пробные оценки, т.е. требует несколько просмотров обучающей выборки для сопоставления с каждой предлагаемой величиной шага соответствующего значения суммарной целевой функции.
Метод сопряженных градиентов,
надстроенный над суммарным градиентом, тоже с адаптацией длины шага на
каждой итерации.
Выбранные методы позволяют сравнить между собой online- и batch-принципы
обучения, оценить эффект от динамической адаптации шага и от использования
быстрых антиовражных методов оптимизации.
Для предварительного определения длины шага для методов 1,2 использовалась эмпирика [8,6] на основе пробного сканирования. В [8,6] вдобавок показана малая чувствительность online-обучения к величине шага: высокая скорость сходимости обеспечивается при величинах шагов из интервала длиной чуть ли не в два порядка, а существенное замедление сходимости или расхождение обучения возникает вне этого широкого интервала. Но для batch-обучения с фиксированным шагом графики из [9] говорят, что интервал оптимальных длин шага может быть очень узким и лежать внутри одного порядка величины, т.е. может требоваться очень детальное сканирование с соответствующим увеличением времени расчета. Тем не менее, метод [8,6] идентификации длины шага показал здесь себя эффективно и для обоих классов алгоритмов применялся с одинаковыми настройками, сначала грубо сканируя интервал значений, а потом детальнее уточняя окрестности вокруг найденного минимума. При этом требовалось порядка 50-80 просмотров выборки и коррекций нейросети.
Результаты экспериментов даны в Таблице 2, где указаны число вычислений градиента и общее число просмотров обучающей выборки, усредненные по 25 пробам. При online-обучении и остановке обучения при достижении заданного уровня точности число просмотров выборки будет в 2 раза больше числа вычислений градиента потому, что после каждой эпохи обучения выполняется вычисление ошибки обучения при зафиксированных адаптивных параметрах сети. При оптимизации шага число просмотров выборки в 5-6 раз превосходит количество вычислений градиента из-за проб нескольких величин шагов на каждой итерации обучения такова процедура динамической оптимизации шага на основе параболической аппроксимации. После коррекции указанных в Таблице 2 чисел просмотров выборки для первых двух методов на величины трудозатрат, необходимых для предварительного определения приемлемой длины шага, можно сделать следующие выводы.
Online-обучение с неадаптивным шагом в 20
из 21 случая быстрее batch-обучения с
неадаптивным шагом (только на задаче Spambase трудозатраты методов
одинаковы), что подтверждает результаты [5,6] о проигрыше обучения по
суммарному градиенту в этой паре алгоритмов.
Batch-обучение с неадаптивным шагом и
batch-обучение с адаптацией шага обычно
требуют сопоставимого числа вычислений градиента, но по общему числу
просмотров выборки случай с адаптацией шага всегда проигрывает, иногда даже
на
порядок. Это означает, что желательно применять не требующую пробных тестов
процедуру оценивания длины шага на каждой итерации.
Использование метода сопряженных
градиентов и других быстрых антиовражных
методов оптимизации значительно ускоряет, по сравнению с обычным
наискорейшим спуском, обучение нейросети. Таким образом, использование более
эффективных, по сравнению с градиентом, направлений не просто компенсирует
негативный эффект множественных проб при одномерной оптимизации, но и
значительно обгоняет по числу просмотров выборки случай обучения по
суммарному градиенту с постоянным шагом.
Online-обучение с фиксированным шагом сопоставимо по эффективности с наиболее сложным из рассмотренных здесь алгоритмов методом сопряженных градиентов, оптимизирующем длину шага на каждой итерации. Online-обучение (с учетом трудозатрат на предварительное определение длины фиксированного шага) выигрывало у сопряженных градиентов на семи задачах из 21 (подтверждая при этом процитированные во Введении слова [7]), в остальных случаях проигрывало меньше, чем оба варианта обучения по суммарному градиенту. В случае online-обучения и использования критерия ранней остановки обучения (требует выполнения дополнительной эпохи тестирования после каждой эпохи обучения) тест не после каждой эпохи обучения, а после двух таких эпох снизит среднее число просмотров выборки на четверть, что позволит еще на двух задачах, а именно, на задачах Letter, Pen digits превзойти метод сопряженных градиентов. Раздел 4 далее показывает возможности дальнейшего ускорения обучения в online-парадигме, поэтому здесь можно сказать, что при batch-обучении привлечение дополнительных мощных методов градиентной оптимизации не позволяет существенно и стабильно превзойти эффективность online-обучения с оптимальным для него шагом: только в единственной задаче Spambase выигрыш составил величину порядка 20 это никак не соответствует оценкам [2] о стабильном выигрыше двух-трёх и более порядков.
Пункты 1,4 представляются наиболее интересными подтверждаются отсутствие необходимости в накоплении суммарного градиента всей выборки и оптимальность проведения коррекции сети после просмотра малого фрагмента выборки (одного примера в рассмотренном случае). Подобный же вывод о необходимости как можно более частой коррекции был получен ранее [10] и в задаче оптимального распараллеливания процесса обучения для многопроцессорной ЭВМ.
Таким образом, многие, во многом эмпирические, выводы, существующие в нейросетевой практике относительно высокой эффективности применения отдельных приёмов из теории оптимизации, являются неверными, как и отмечено в [5,6].
4. Способы ускорения обучения и другие вопросы
Для обучения с постоянным шагом (как в online-, так и в batch-парадигмах) предварительное определение длины фиксированного шага может быть заменено процедурой "Bold driver" [11] адаптации шага от итерации к итерации. Алгоритм "bold driver" ускоряет обучение по сравнению с использованием фиксированного шага, но в данной работе эти результаты не приводятся из-за обнаруженной необходимости оптимизации настроек алгоритма под каждый способ обучения (online- и batch-) по отдельности, чтобы в среднем по набору задач настройки алгоритма максимизировали скорость обучения и минимизировали амплитуду колебаний эффективности. Более того, эксперименты автора и здесь показывают желательность стохастизации обучения путём повышения степени оптимистичности настроек алгоритма "bold driver".
Результаты тестирования обученных сетей на независимых тестовых выборках во многом подтверждают выводы [12,13] о том, что batch-обучение с оптимизацией шага и особенно эффективные методы оптимизации типа сопряженных градиентов часто приводят к переобучению нейросети. Однако, поскольку всего 5 задач из 21 имеют тестовые выборки, то утвердительно подтверждать эти результаты и приводить их здесь не представляется возможным. Для online-обучения же с фиксированным шагом результаты [8] говорят о снижении ошибки обобщения с уменьшением шага, что тоже указывает на нежелательность адаптации шага, но широкий интервал близких к оптимальным значений шага при обучении в online-парадигме позволяет легко максимизировать как скорость обучения, так и последующие обобщающие способности нейросети путем выбора наименьших значений шагов из тех, при которых наблюдается высокая скорость обучения [8].
Эффективность свободных от оптимизации шага квазиньютоновских методов для обучения нейросети исследована недостаточно: использование метода Дэвидона в [14] нельзя признать успешным, поскольку оперирование с оценкой полной обратной матрицы Гессе в нейросетях даже среднего размера (тысяча и более адаптивных переменных в сети с несколькими десятками нейронов) может приводить к негативным численным эффектам. Да и эксперименты [14] проводились на единственной реальной задаче не ясны степень и стабильность ускорения обучения при применении этого метода. Поэтому при обучении нейросетей алгоритмами оптимизации со сверхлинейной сходимостью, фактически, единственным способом избавления от процедуры оптимизации шага является применение псевдоньютоновского метода [4], явно вычисляющего диагональ матрицы Гессе, при увеличении длительности каждой эпохи обучения примерно в 1.5 раза (к прямому и обратному распространению сигналов по сети добавляется еще обратное распространение вторых производных). А обращение диагональной матрицы тривиально.
Способы же специального предварительного или динамического отбора малого числа обучающих примеров из всей обучающей выборки (например, методы [15-18]) применимы ко всем алгоритмам обучения. Переформулирование целевой функции как зависящей еще и от величины шага (для возможности вычисления градиента и по этому показателю [19]) тоже не вносит ограничений на собственно алгоритм коррекции. Поэтому перспективы ускорения обучения (при одновременном избавлении от эффекта переобучения нейросети) лежат преимущественно в области online-алгоритмов обучения, стохастизации алгоритмов обучения и управления шагом коррекции. Возможно введение отдельного значения шага для каждого адаптивного коэффициента нейросети ([4,9,20] и др.) возвращение к локальности правил управления коррекцией значений адаптивных переменных, т.е к базовому архитектурному принципу нейросеть обучает сама себя вместо заместившего его принципа надстройки внешнего учителя, управляющего обучением нейросети путем указания векторов поправок (соответствующих отличным от направления градиента направлениям коррекции) и/или значений шагов коррекции.
Заключение
Эксперименты показывают сравнимую практическую эффективность ростейшего метода попримерной градиентной адаптации нейросети с постоянным шагом коррекции и одного из наиболее эффективных для задач большой размерности методов градиентной оптимизации метода сопряженных градиентов с одномерной оптимизацией шага на каждой итерации спуска. Подтверждено, что использование суммарного градиента проигрывает по эффективности обучения по сравнению с коррекцией вдоль градиентов отдельных примеров. Показано, что поисковые методы одномерной оптимизации шага приводят к значительному росту накладных расходов при обучении. Недавние теоретические результаты [21] дают дополнительную информацию о том, какими должны быть оптимальные методы online- и batch-обучения, и доказывают асимптотическое превосходство попримерного обучения, в том числе и возможность достижения для него минимума ошибки обобщения после единственного прохода по обучающей выборке.
Литература
1. Осовский С. Нейронные сети для обработки информации. - М.: Финансы и
статистика, 2002. 344с.
2. Gilev S.E., Gorban A.N., Mirkes E.M. Several methods for accelerating the
training process of neural networks in pattern recognition / Preprint №146Б.
Institute of biophysics USSR Acad. Sci, Sib Branch. Krasnoyarsk, 1990. 16p.
3. Becker S., LeCun Y. Improving the convergence for back-propagation learning
with second order methods / Proc. 1988 Connectionist Models Summer School.
Morgan
Kaufmann, 1989. pp.29-37.
4. Battiti R. First- and second-order methods for learning: between steepest
descent and Newton’s method / Neural Computation, 1992. Vol.4. No.2. pp.141-166.
5. Wilson D.R., Martinez T.R. The inefficiency of batch training for large
training sets / Proc. Int. Joint Conf. Neural Networks (IJCNN’2000), Como, Italy,
2000. Vol.2. pp.113-117.
6. Wilson D.R., Martinez T.R. The general inefficiency of batch training for
gradient descent learning / Neural Networks. 2003, Vol.16. Issue 10.
pp.1429-1451.
7. LeCun Y., Simard P.Y., Pearlmutter B. Automatic learning rate maximization by
on-line estimation of the Hessian’s eigenvectors / Advances in Neural
Information Processing Systems 5 (1992). Morgan Kaufmann, 1993. pp.156-163.
8. Wilson D.R., Martinez T.R. The need for small learning rates on large
problems / Proc. Int. Joint Conf. Neural Networks (IJCNN’2001), Washington, DC,
USA. 2001. pp.115-119.
9. Riedmiller M. Advanced supervised learning in multi-layer perceptrons from
backpropagation to adaptive learning algorithms / Computer Standards and
Interfaces,
1994. Vol.16. pp.265-278.
10. Torresen J., Tomita S., Landsverk O. The relation of weight update frequency
to convergence of BP / Proc. World Conf. Neural Networks (WCNN’1995), Washington,
DC, USA. 1995. pp.679-682.
11. Battiti R. Accelerated backpropagation learning: two optimization methods /
Complex Systems, 1989. Vol.3. pp.331-342.
12. Fukumizu K. Effect of batch learning in multilayer neural networks / Proc.
5th Intl. Conf. Neural Information Processing (ICONIP1998). 1998. pp.67-70.
13. Lawrence S., Giles C.L. Overfitting and neural networks: conjugate gradient
and backpropagation / Proc. Int. Joint Conf. Neural Networks (IJCNN’2000), Como,
Italy. 2000. pp.114-119.
14. Beigi H.S.M. Neural network learning through optimally conditioned
quadratically convergent methods requiring no line search / Proc. 36th Symposium
on Circuits and
Systems, Detroit, Michigan, USA, 1993.
15. Röbel A. Dynamic pattern selection for faster learning and controlled
generalization of neural networks / Proc. European Symposium on Neural Networks
(ESANN’1994), Brussels, Belgium, 1994. pp.187-192.
16. Engelbrecht A.P., Cloete I. Selective learning using sensitivity analysis /
Proc. Int. Joint Conf. Neural Networks (IJCNN’1998), Anchorage, Alaska, USA,
1998. pp.1150-1155.
17. Hara K., Nakayama K., Kharaf A.A.M. A training data selection in
online-training for multilayer neural networks / ibid. pp.2247-2252.
18. Rimer M.E., Andersen T.L., Martinez T.R. Speed training: improving the rate
of backpropagation learning through stochastic sample presentation / Proc. Int.
Joint Conf.
Neural Networks (IJCNN’2001), Washington, DC, USA. 2001. pp.2661-2666.
19. Zhang Y. Updating learning rates for backpropagation networks / Proc. Int.
Joint Conf.Neural Networks (IJCNN’1993), Nagoya, Japan. 1993. Vol.1. pp.569-572.
20. Jacobs R. Increased rates of convergence through learning rate adaptation /
Neural Networks, 1988. Vol.1. pp.295-307.
21. Bottou L., LeCun Y. Large scale online learning / Advances in Neural
Information Processing Systems 16 (2003). MIT Press, 2004. pp.217-224.