Общие правила и стратегии разработки связанных систем
Yann le Cun
Перевод с английского: Умяров Н.Х.
Аннотация
Интересное свойство связанных систем - способность обучаться по примерам. Хотя самые последние работы концентрируются на сокращение времени обучения, наиболее важное преимущество обучающей машины - обобщение производительности. Считается, что хорошая производительность в реальных задачах обобщения не может сохраняться без предварительных знаний о разрабатываемой задаче в системе. Сети обратного распространения ошибки (back-propagation) обеспечивают способ задания таких знаний путем введения ограничений как на архитектуру сети, так и на ее веса. В общем случае, могут рассматриваться некоторые ограничения, в частности, специфические преобразования пространства параметров.
Построение связанной сети с ограничениями для распознавания изображений представляется посильной задачей. Мы опишем маленькую проблему распознавания рукописных цифр и покажем, что хотя проблема линейно разделима, однослойная сеть получается с плохой производительностью. Связанная многослойная сеть с ограничениями выполняется очень хорошо на этой задаче, когда организуется иерархическая структура с обнаружением сдвигов (изменений) инвариантных признаков, свойств.
Эти результаты подтверждают идею, что минимизация числа свободных параметров в сети увеличивает обобщающую характеристику сети.
1 Введение
Связные архитектуры привлекли значительное внимание в последние годы, так как они обладают рядом интересных свойств. Среди многочисленных обучающих алгоритмов, которые были предложены для комплексных связных сетей, алгоритм обратного распространения ошибки являются наиболее широко распространенными. Обратное распространение было предложено в 1986 году, но был разработан несколькими независимыми группами в разных контекстах и для разных задач (Бризон и Хо, 1969; Вербос, 1974; Ле Кун, 1985; Паркер, 1985; Ле Кун, 1986). Было указано использовать сеть для оптимального управления и систем идентификации. Некоторые могут доказывать, что базовой идеей использования обратного распространения была оптимизация контроля, пока машина обучается (Ле Кун, 1988).
Для измерения могут быть рассмотрены две характеристики, которые во время обучения алгоритм узнавал - это скорость и обобщающая характеристика. Обобщение - главное свойство, которое может быть найдено, оно определяет количество данных, нужных для тренировки системы так, чтобы система выдала правильный ответ, когда представленный шаблон не попадает в пределы обучающего множества. Мы увидим, что скорость обучения и обобщение тесно связаны. Хотя разные успешные приложения на сети обратного распространения ошибки описаны в литературе, условия, при которых будет хорошее обобщение производительности, не известно. Считается, что обратное распространение ошибки - общее правило, которое может использоваться как черный ящик для разных проблем и, конечно, представляются желаемыми. Хотя некоторые средние проблемы могут быть решены использованием неструктурированных сетей, мы не можем надеяться, что такую сеть можно будет использовать для решения любой проблемы. Главной целью данного документа - показать, что хорошее обобщение производительности может быть достигнуто, если у нас имеются знания о решаемой задаче на данной сети. Хотя, в общем случае, некоторые знания могут быть достаточно сложными, они хорошо подходят к таким задачам, как распознавание изображений и речи.
Приспособление сетевой архитектуры для решения задач может быть обдумано изменением размера пространства возможных функций, которые сеть может генерировать без чрезмерного объема вычислительной мощности. Теоретические учения (Денкер, 1987) (Патанелло и Карневах, 1987) показал, что вероятность правильного обобщения зависит от размера пространства гипотез (принимается во внимание общее число сетей) и размера обучающей выборки. Если пространство гипотез слишком большое и/или размер обучающей выборки маленький, тогда будет большое число сетей, которые совместимы с обучающими данными. Обратно же, если требуется хорошее обобщение при увеличении архитектуры сети, размер обучающей выборки может быть тоже увеличен. В особенности, требуемое число примеров масштабируются в логарифмической зависимости от числа функций, которые сетевая архитектура может включать.
2 Преобразования пространства весов
Сокращение числа свободных параметров в сети не обязательно подразумевает снижение размера сети. Некоторые технологии, например общие веса, описывают для решения так называемых проблем Т-С и может использоваться для построения сети меньшего размера (уменьшением числа свободных параметров).
По факту, 3 главные технологии могут быть использованы для построения сокращенной сети.
Первая технология - проблемно-независима и заключается в динамическом удалении ненужных связей в течение обучения. Это может быть совершено добавлением термина стоимости функции, которая наказывает большие сети с большим числом параметров. Некоторые авторы описали схемы, обычно включающие непропорциональные распады весов (Румелхарт, 1988), (Чаувин, 1989, Хансон и Пратт, 1989) или использование пропускного механизма для коэффициентов (Мозер и Смоленский, 1989). Производительность обобщения может быть использована для увеличения значительных или мелких проблем. В этом процессе могут возникать две помехи: требуется идеальная настройка отсеченных коэффициентов для предотвращения катастрофических эффектов и также значительное падение сходимости.
2.1 Общие веса
Вторая технология - общие веса. Общие веса - наличие нескольких связей (ссылок), которые управляются одним параметром (весовой коэффициент). Общие веса могут быть интерпретированы как представление равенства среди сильных соединений. Интересная особенность общих весов - они могут реализовываться с очень низкими вычислительными затратами. Это общая парадигма, которая может использоваться для описания TDNN (time delay neural network - нейронная сеть с временными задержками) для распознавания речи, развернутых рекуррентных сетей, для выделения инвариантных слоев.
2.2 Общее преобразование пространства весов
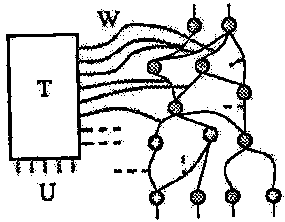
Третья технология, которая обобщает понятие общих весов - преобразование пространства весов (WST) (Ле Кун, 1988) WST базируется на факте, что поиск, выполняемый процедурой обучения, не должен делаться в полносвязном пространстве, который подходит для задачи. Это может быть архивом при условии, что сильные связи могут быть вычислены из параметров через преобразование, и предвидит, что матрица Якоби этого преобразования известна, поэтому, мы можем вычислить части целевой функции по параметрам. Градиент стоимостной функции в отношении параметров есть произведение матрицы преобразования на градиент связи по сильным сторонам. Это иллюстрирует рисунок 1.

Рисунок 1 - Преобразования пространства весов
3 Пример: небольшая проблема распознавания цифр
Следующие эксперименты показывают стратегии разработки сетей для специфических задач. Задача, описанная ниже не является реальным приложением, но этого достаточно для понимания сути проблемы. Средний размер базы данных делает задачу нетривиальной, но также позволяет построить исчерпывающее число тестов скорости обучения и увеличения производительности.
3.1 Описание задачи
База данных является композицией 480 примеров цифр, представленных изображением в виде 16 на 16 пикселей. 12 примеров каждой из 10 цифр были написаны от руки одним человеком на 16 * 13 bmp с использованием мыши. Каждое изображение обычно использовалось для генерации 4 примеров помещением оригинального изображения в 4 последовательные горизонтальные позиции 16 * 16 bmp. Обучающее множество формируется выбором 32 примеров каждого класса цифры случайно среди 480 изображений, остальные 16 примеров используются в тестируемом множестве. Так, обучение осуществляется на 320 изображениях, а тестирование - на 160. На рисунке 2 представлены некоторые из обучающих примеров.

Рисунок 2 - Некоторые примеры входных образцов
3.2 Установки эксперимента
Все опыты были произведены в BP симуляторе SN (Боттоу и Ле Кун, 1988). Каждый нейрон сети вычисляет скалярное произведение между входным вектором и вектором весов. Из этой суммы вычитается ai для модуля i, затем проходит через функцию активации - сигмоид для производства состояния модуля i, обозначаемое xi:
xi = f (ai)
Функция активации - масштабированный гиперболический тангенс:
f (a) = A tanh Sa
где A - амплитуда функции и S - определяет ее наклон в оригинале, f - нечетная функция с горизонтальными ассимптотами +A и -A.
Симметричные функции предполагают получение более быстрой сходимости, несмотря на то что обучение может стать чрезвычайно медленным, если веса слишком маленькие. Причина этой проблемы в том, что начальные значения пространства весов - стабильная точка для обучения в динамике и, хотя это точка перевала, она является привлекательной в большинстве направлений. Для наших вычислений мы используем A=1.7159 и S = 2/3. С этими параметрами мы получаем удовлетворительные для нас значения функции f(1) = 1 и f(-1) = -1. Мы получаем общее усиление функции активации вокруг окресности 1 в обычных условиях и интерпретация состояний сети упрощается. Более того, абсолютное значение второй производной функции f будут максимальными в точках +1 и -1, которые улучшают сходимость в конце этапа обучения.
Перед этапом обучения, веса инициализируются случайными значениями, используя равномерное распределение между -2.4/Fi и 2.4/Fi, где Fi - число входных элементов (нагрузочная способность по входу), с соединениями. С несколькими соединениями, разделяющих веса, это правило сложно применить, но в нашем случае все связи разделяют один и тот-же вес среди модулей с идентичными нагрузочными способностями по входу. Если начальные значения весов слишком маленькие, градиенты слишком малы и обучение долго длится, а если начальные значения весов большие, то сигмоиды являются насыщенными и градиент также очень маленький. Стандартное отклонение взвешенной суммы масштабируется как квадратный корень от числа входных сигналов, когда они независимы и масштабируются линейно, если входные сигналы сильно кореллируют между собой. Мы выбираем вторую гипотезу, по которой модули получают высококореллированные входные сигналы.
Дальше, если мы говорим о слоях сетей, мы ссылаемся на число слоев, модифицируемых весов. Таким образом, сеть с одним скрытым слоем является двухслойной сетью.
3.3 Net-1: Однослойная сеть
Простейшая сеть, которая может решить нашу задачу, является однослойная сеть, полносвязная сеть с 10 сигмоидами на выходе (2570 весов, включая смещение). Такая сеть успешно обучается на обучающем множестве, которое означает, что проблема - линейно разрешима. Но, даже, если обучающее множество обучает отменно, производительные характеристики падают - 80% и 72% распознавание показали полностью обученные сети, когда остановили обучение (см. рис. 3, Net-1). Интересно, что производительность на тестируемом множестве достигает максимума слишком рано, а потом постепенно падает. Этот феномен описан многими авторами и выходит за рамки данной статьи. В результате, становится видно, что наша сеть не может распознать даже тривиальные ситуации, так как система согласованных фильтров создает усредненный шаблон, формируемый наложением обучаемых примеров.
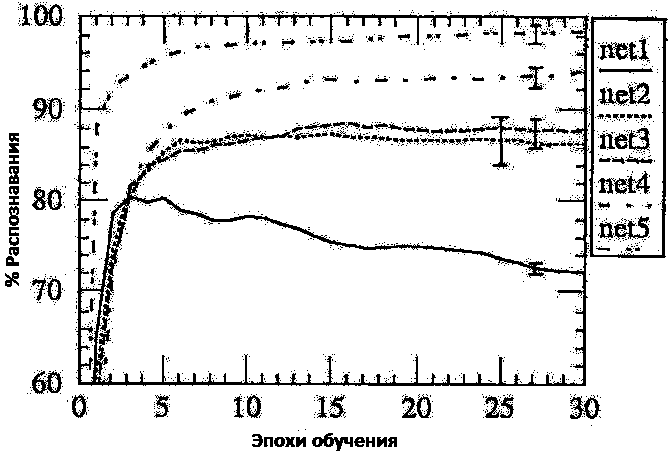
Рисунок 3 - Производительность и время обучения для 5 архитектур сетей: Net-1: однослойная сеть, Net-2: 12 скрытых нейронов являются полносвязными, Net-3: 2 скрытых слоя локально связаны, Net-4: 2 скрытых слоя, локально связаны с ограничениями, Net-5: 2 скрытых слоя, локальные связи, 2 уровня связей с ограничениями.
3.4 Net-2: Двуслойная полносвязная сеть
Вторым шагом можно добавить скрытый слой между входом и выходом сети. 12 скрытых нейронов, полносвязных и со входом, и с выходом. Всего 3240 весов, включая смещение. предсказуемо, эта сеть может обучаться очень хорошо за несколько эпох (между 7 и 15). Эпоха - один проход по обучаемому множеству. Обобщительная характеристика лучше, чем в сети Net-1, достигает 87% успешного распознавания, после 6 эпох обучения (см. рис. 3, Net-2). Также наблюдался легкий эффект переобучения, который имел значительно меньший размах по сравнению с предыдущей сетью. Интересно отметить, что стандартное отклонение по обобщенной производительности больше, чем в первой сети. Это значит, что сеть более недетерминированна и число решений, которые согласуются с обучающим множеством - слишком большое. К несчастью, эти разные решения не дают эквивалентных результатов на тестовом множестве. Этот результат показывает, что наша сеть слишком большая, или имеет большое число степеней свободы.
3.5 Net-3: Локально связанные 3-слойные сети
Часто изменение размера сети также изменяет ее общую часть, некоторые знания о задаче понадобятся для сохранения способности сети решать задачу. Простое решение нашей перенасыщенной параметрами задачи, может быть найдено, если мы помним, что сеть должна распознавать изображение. Классическая работа визуального шаблона распознавания образов должна демонстрировать преимущества выделение локальных свойств и комбинировать их для формирования высшего уровня свойств (признаков). Архитектура сети включает 2 скрытых слоя, так называемых H1 и H2. Первый скрытый слой, Н1 - двумерный массив 8*8. Каждый нейрон в Н1 получает свой вход из девяти нейронов входного слоя, расположенного в окресности 3 на 3. Для нейронов Н1-го слоя, которые отстают друг от друга, рецептивные поля (во входном слое) являются отдельными двумя пикселями в отдалении. Так, рецептивные поля двух соседних скрытых узлов перекрываются один другим по строке/столбцу. Информация будет компактно с помощью множителя-посредника (уплотняется в 4 раза) от входа к слою H1.
Слой Н2 - плоскость, размерами 4*4, но рецептивные поля уже имеют размеры 5*5. Н2 - полносвязная сеть с 10 выходами. Сеть имеет 1226 связей (см. рис. 4).

Рисунок 4 - Три нейросетевые архитектуры: Net-1, Net-2 и Net-3
Производительность немного лучше, чем в Net-2, достигается распознавание в 88,5% случаев, но мы добиваемся значительной экономии вычислительных ресурсов - в 3 раза по сравнению с Net-2. Также следует помнить, что среднеквадратичное отклонение производительности в сети Net-3 меньше, чем в сети Net-2.
3.6 Net-4: Ограниченная сеть
Одной из главнейших проблем распознавания изображений - характерные признаки изображения могут появиться в разных местах входного изображения. Поэтому будет полезным иметь детекторы признаков, которые смогут определять конкретные образцы признаков в любой точке входной плоскости. Так как точное местоположение признаков не имеет значения к классификации, мы можем позволить себе потерять некоторые позиции информации в процессе. Тем не менее, приблизительная информация должна быть сохранена с тем, чтобы в следующем слое ей можно было воспользоваться для выявления признаков высшего порядка.
Распознавание признаков в любой точке входного изображения может быть легко сделано использованием общих весов. Первый скрытый слой может состоять из нескольких плоскостей, которые мы назовем картами признаков. Все нейроны плоскости разделяют одинаковое множество весов, тем самым определяя одинаковые признаки в разных позициях. Поскольку точное расположение признаков не важно, карты признаков не должны быть такими большими, как входные изображения. Интересен побочный эффект этой технологии: она снижает число свободных весов в сети.
Архитектура сети Net-4 очень похожа на Net-3, данная сеть включает в себя также два скрытых слоя. Первый скрытый слой состоит из двух карт признаков размерами 8*8. Каждый нейрон карты признаков принимает на вход область изображения размерами 3*3. Для нейронов в карте признаков, которые являются одной единицей друг друга, их рецептивные поля являются субдискретизованы. Главное отличие от сети Net-3 - все нейроны карты признаков разделяют множество из девяти весов (но каждый из них имеет независимое смещение). Технология субдискретезации преследует две цели. Первая - поддержать размер сети в разумных пределах. Вторая - для обеспечения гарантии, что некоторая информация будет отброшена в процессе распознавания признаков.
Даже если распознавание признаков является инвариантным к сдвигам, это не означает, что операция, выполняемая коллективно, будет выполняться. Когда входное изображение сдвигается, выход карт признаков также сдвигается, иначе - также не меняется. Когда сдвиг входа небольшой, выход карт признаков не сдвигается, но немного деформируется из-за субдискретизации.
Как и в предыдущей сети, Н2 - плоскость, размерами 4*4, но рецептивные поля уже имеют размеры 5*5. Выходной слой - полносвязный со вторым слоем и имеет 10 нейронов. Сеть имеет 2266 связей, но только 1132 (свободных) весов (см. рис. 5).
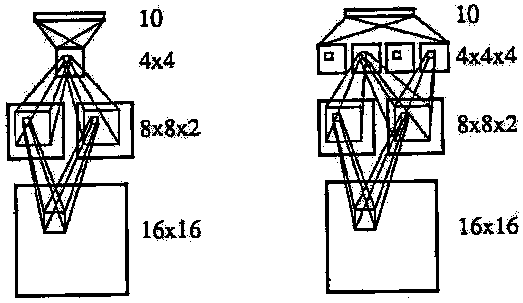
Рисунок 5 - Две нейросетевые архитектуры с общими весами: Net-4 и Net-5
Качество распознавания для этой сети составляет порядка 94%, это говорит о том, что использование инвариантности признаков полезно для решения этой задачи. Этот результат также говорит о том, что несмотря на маленькое число независимых весов, вычислительная сила сети повышается.
3.7 Net-5: Сеть с иерархическим выделением признаков
Подобная идея может быть развернута дальше, с указанием использовать иерархическую структуру с несколькими уровнями ограниченных карт признаков.
Архитектура сети Net-5 является очень простой в сравнении с Net-4, предполагается второй скрытый слой Н2 был заменен четырьмя картами признаков, каждая из которых является плоскостью размерами 4*4. Нейроны этого слоя имеют рецептивное поле размером 5*5 в первом скрытом слое. Также, все нейроны в картах признаков разделяют тоже множество 25 весов и имеют независимые смещения. И снова, субдискретизация два-к-одному имеет место между первым и вторым слоями сети.
Сеть имеет 5194 связей, но только 1060 свободных параметров, наименьшее число среди всех сетей, описанных в данной статье (см. рис. 5).
Распознавание происходит с точностью 98.4% (дважды было достигнуто 100% распознавание в десяти попытках) и увеличивается чрезвычайно быстро в начале обучения. Это предполагает, что используя несколько уровней ограниченных карт признаков является большой помощью для достижения инвариантности к сдвигам.
4 Обсуждение
Результаты объединены в таблицу 1.
Таблица 1: Обобщение производительности на 5 разных архитектурах сетей

Как и следовало ожидать, обобщенная производительность повышается с уменьшением числа свободных параметров сети. Достойным внимания исключением является результат однослойной сети и двуслойной полносвязной сетью. Даже когда двуслойная сеть имеет больше параметров, производительность значительно лучше. Одно объяснение может заключаться в том, что однослойная сеть не может классифицировать полное множество (обучающее и проверочное) корректно, но эксперименты показывают, что это возможно. Мы видим два разных возможных объяснения. Первое заключается в том, что знание неявным образом добавляется в скрытый слой: мы сообщаем системе, что проблема не первоочередная. Второе объяснение - эффективность процедуры обучения (как определено Денкером в 1987 году) лучше в двухслойной сети, чем в однослойной, это означает, что больше информации может быть извлечено из каждого примера с шаблоном. Это сложная теория должна быть изучена в дальнейшем.