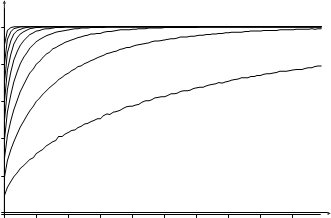
Рисунок 1. – Зависимости достоверности результатов D от сложности распознавания Sl и репрезентативности данных.
Источник: Сайт компании Vidicon
Распознавание образов является процессом, которым можно управлять, изменяя поток поступающей информации или выбирая методы распознавания и их характеристики [1]. Описанная в работе [1] модель системы управления процессом распознавания в реальном времени показывает, что, изменяя параметры управления, можно добиваться требуемых результатов системы распознавания образов (СРО) по достоверности и производительности. В качестве критерия эффективности при управлении процессом распознавания в системах реального времени лучше использовать компромисс между уровнем достоверности распознавания образов и производительностью работы, определяющийся значением некоторых (например, стоимостных) затрат [1]:
где ∆tω – интервал времени, потраченный на распознавание образа ωx; ∆t – ограничивающий интервал времени; Dз, D – соответственно заданное и фактическое значение достоверности распознавания; Pз, P – соответственно заданная и фактическая производительность работы СРО реального времени.
В данной работе предлагается подход к расчѐту эффективности СРО реального времени путѐм оценки достоверности и производительности.
Рассмотрим некоторую вычислительную систему, на которой в реальном времени одновременно распознаются 1 или более образов. Пусть условием к работе системы является необходимость распознать эти образы с достоверностью большей либо равной Dз за минимальное время. Различные образы можно распознавать с уровнем Dз за разное время. В работе [1] показано, что в зависимости от сложности распознавания образов можно выбирать различное количество информации для обеспечения уровня Dз в каждом конкретном случае. На рисунке 1 изображены зависимости достоверности результатов от сложности распознавания и репрезентативности данных для двух образов с нормальными распределениями признаков.
Понятие сложности распознавания характеризует меру близости образов и определяется, как вероятность ошибки распознавания [1] при объѐме характеризующих объект данных N равном 1.
Как видно из рисунка 1, для Dз = 0,9 образы с различной сложностью можно распознать при разном объѐме данных N. Зная сложность распознавания образов можно выбирать такие режимы работы СРО, при которых Dз ≤ D и объѐм данных для распознавания минимален.

Рисунок 1. – Зависимости достоверности результатов D от сложности распознавания Sl и репрезентативности данных.
Основным вопросом при применении описанного подхода к выбору режима. распознавания является определение значения сложности распознавания конкретного образа. В идеале при решении задачи на вход должны поступать не только признаки неизвестного образа, но и его сложность распознавания. На практике это трудно осуществимо, т.к. обычно для того, чтобы оценить значение сложности распознавания образа, необходимо его идентифицировать. Однако можно использовать сложность распознавания предыдущего образа для распознавания текущего образа. Данный подход применим в случае, когда на СРО в потоке через интервал времени поступают порциями неизвестные образы, причѐм изменение образов в потоке происходит постепенно. Такая ситуация возможна, например, при анализе видеопотока с видеокамеры, геофизических исследованиях скважин [2] и т.п. Негативным эффектом от описанного подхода является то, что, при переходе от анализа образа с малой сложностью распознавания к большей, может возникнуть ситуация, когда система работает в режиме Dз > D. Поэтому необходимо оценить эффективность управления процессом распознавания образов.D Sl=0,1;0,2;0,3;0,4;0,5;0,6;0,9.
Допустим, что на СРО реального времени поступают неизвестные образы из возможной группы образов:
Дгде K > 1 – количество классов образов, а вероятность их появления не зависит от номера испытания. Тогда последовательность образов, поступающих на СРО, можно описать однородной цепью Маркова [3]. Матрица переходов последовательности на шаге 1 описывается следующим образом: условная вероятность перехода из i-го состояния в j-ое. Номер состояния характеризует режим СРО для анализа образа с тем же номером.
Режим характеризуется объѐмом данных для распознавания в соответствии с выражением (2) и рисунком 1. При установившемся режиме СРО в одном состоянии D ~ Dз, поэтому матрица статистического уровня достоверности при переходе из одного состояния в другое имеет следующий вид Для того, чтобы вычислить безусловную вероятность появления каждого образа достаточно рассчитать матрицу перехода за L шагов (где вычисляется согласно следующему выражению [3]. Результирующая матрица будет содержать одинаковые строки с безусловными вероятностями для каждого состояния
Согласно теореме умножения вероятностей [3] можно найти вероятность каждого перехода в выражении (3), которая будет равна произведению безусловной вероятности состояния на условную вероятность перехода в то же или другое состояние. Данные вероятности необходимы для определения среднего значения достоверности распознавания образов:
Производительность работы СРО напрямую связана с объѐмом анализируемых данных, поэтому достаточно вычислить средний объѐм данных на распознавания одного образа для оценки производительности:

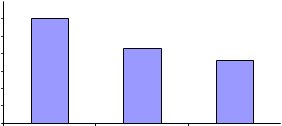
Рисунок 2. – Достоверность распознавания и средний объём данных для режимов СРО: без управления
Зная показатели достоверности и производительности работы СРО не сложно вычислить режим, удовлетворяющий (1), для этого необходимо знать показатели функций затрат:
Z = Z0 + Z1(N ) + Z 2 (1 - D) , (12)
где Z0 – затраты независящие от производительности и достоверности распознавания СРО, Z1 – затраты, обусловленные производительностью, Z2 – затраты обусловленные ошибками при распознавании образов.
Описанный подход позволяет оценить возможность применения методики управления процессом распознавания образов в реальном времени и возможный эффект от применения.
Литература
1. Кручинин, А.Ю. Управление процессом распознавания образов в реальном времени / А.Ю. Кручинин // Автоматизация и современные технологии. –
2010. – №3. – С. 33-37.
2. Кручинин А.Ю., Аралбаев Т.З. Оптимизация геофизических исследований скважин на основе многофакторной имитационной модели // Вестник Самарского государственного университете, серия «Технические науки».
2007. № 2 (20).
3. Гмурман, В.Е. Теория вероятностей и математическая статистика / В.Е.
Гмурман. М. : Высш. шк., 2004. 479 с.