Проведен анализ напряженно-деформированного состояния разрушенных горных пород с учетом критерия Кулона Мора методом конечных элементов. В последние годы значительный рост информационных технологий обусловил широкое применение компьютерной техники для анализа напряженно-деформированного остояний тел в различных отраслях науки. Для этой цели применяются различного рода расчетные пакеты, основанные на численных методах решения. Наиболее распространенным из них является метод конечных элементов (МКЭ) или метод Ритца. Хотя основные принципы МКЭ сформулированы давно, широкое распространение метод получил во второй половине двадцатого столетия, что связано с развитием вычислительной техники. Несмотря на свою популярность, этот метод, равно как и любой другой вариационный метод, имеет существенный недостаток сложность получения априорных оценок. Поэтому для применения метода с достаточной точностью, необходимо производить сравнение каждой расчетной программы с экспериментальными данными, то есть, необходима верификация модели. При решении вопросов горной геомеханики зачастую возникает необходимость смоделировать некоторую область массива, представленную разрушенными или дискретизированными породами. На пример, при моделировании зоны разрушенных пород (ЗРП) или искусственных охранных сооружений из рядовой породы. В этом случае использование упругой линейной модели, априори заложенной в МКЭ, когда напряжения пропорциональны деформациям, а поведение материала описывается законом Гука, не является корректным. Энергетическая теория прочности, широко применяемая для металлов, также не подходит для горных пород. В механике грунтов и строительной механике для материалов с хрупким разрушением рекомендуется использовать критерий, предложенный Кулоном, совпадающий с условием пластичности Треска: i j c = 2, где j, i, j = 1, 2, 3; 3, 2, 1 – главные напряжения, МПа; с – const. Разрушение, согласно этому условию происходит при достижении максимальными касательными напряжениями некоторой физической константы пород с. Эта закономерность известна также как теория прочности Кулона-Мора l = c + tgl, (1) где с – сцепление, количественно равное пределу прочности среды на срез при отсутствии нормальных напряжений, МПа; l – угол внутреннего трения, град. Применительно к дискретным несвязным средам, коэффициент сцепления равен нулю, и выражение (1) показывает, что разрушение (движение) сыпучих сред произойдет, когда максимальное касательное напряжение в данном месте выйдет за огибающую кругов Мора [1].

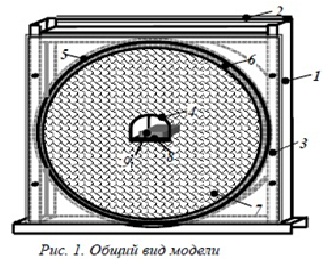
Для проверки верности приведенных выше соображений авторами было проведено математическое моделирование процесса выдавливания дискретизированных пород почвы в полость выработки, обусловленного нарушением равновесного состояния системы «крепь зона разрушенных пород-окружающий породный массив» в результате проведения подрывки почвы без применения и с применением механического отпора этому процессу. При этом в качестве эталона были приняты результаты экспериментов на структурных моделях, проведенных в лабораторных условиях. Целью лабораторных исследований на структурных моделях было установление влияния механического отпора выдавливанию пород почвы горных выработок на характер их смещения в процессе формирования зоны разрушенных пород вокруг выработки. Модель (рис. 1) с масштабом моделирования 1:30, представляла собой сварную металлическую конструкцию (1) со швеллера [60 размерами 0, 720, 52 м, к которой крепилась задняя (2) и прозрачная передняя (3) стенки. Внутри конструкции размещался макет выработки арочного сечения (4) размерами 0,10,15 м, а также металлическая полоса (5), выгнутая в виде круга, шириной равной толщине модели. Эта полоса устанавливалась как ограничитель, определяющий границу зоны разрушенных пород вокруг выработки. Выработка и ограничитель жестко крепились к каркасу и задней стенке модели. По периметру ограничителя, для имитации давления на внешней границе ЗРП, улаживалась пневмокамера (6). В рабочую полость модели помещался объем породы (7) с размером фракции 0,003–0,01 м. На почве выработки для обеспечения равномерной пригрузки по ее поверхности размещалась деревянная пластина (8), на которую устанавливался груз (9). Математическое моделирование проводилось методом конечных элементов с использованием программного комплекса ANSYS. Задача решалась в объемной постановке. В силу осесимметричности задачи моделировалась половина сечения вдоль вертикальной оси (рис. 2).

На основании проведенных исследований можно сделать вывод, что учет в расчетной модели критерия Кулона-Мора позволяет более качественно описать деформационные процессы в разрушенных породах и при наличии исходных данных с помощью МКЭ с большой достоверностью можно моделировать разрушенные породы и сыпучие тела.


1. Ершов Л.В., Либерман Л.К., Нейман И.Б. «Механика горных пород» – М.: Недра, 1987. – 192 с.
2. Касьян Н.Н., Негрей С.Г., Сахно И.Г. О влиянии механического отпора выдавливанию пород почвы горных выработок на их смещения // Разработка рудных месторождений. – 2004. – Вып. 87. – С. 28–29.