Назад в библиотеку
УДК 622.45

СИММЕТРИЯ ДИАГОНАЛЬНОГО СОЕДИНЕНИЯ

Авторы: Трофимов В.А.

Источник: І Известия Донецкого горного института. 2005, № 2. – с. 16–17.


В статье рассматривается возможность точного аналитического расчета аэродинамического сопротивления диагонального соединения из пяти ветвей и особенности трансформации таких вентиляционных соединений.

Анализ особенностей определения аэродинамического сопротивления диагонального соединения [1], состоящего из пяти ветвей, показал, что в некоторых случаях существует возможность точного аналитического расчета этой величины по величинам сопротивлений отдельных ветвей. Рассмотрим условия такого решения (рис.1). Допустим, что диагональное соединение состоит из двух элементарных вентиляционных контуров.

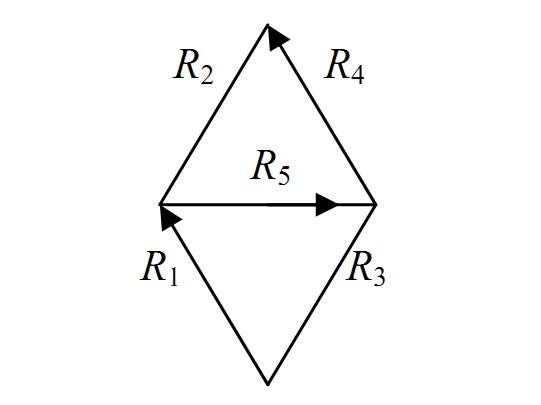
Рис. 1 – Схема диагонального соединения

Для них можно записать следующие уравнения

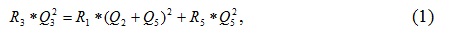
где R1, R2, R3, R4, R5 – аэродинамические сопротивления ветвей составляющих вентиляционное соединение;
Q1, Q2, Q3, Q4, Q5 – расходы воздуха в ветвях диагонального соединения. Разделим все члены этих уравнений на Q5–2 и примем условие, что Q3/Q5=Q2/Q5=Х. Это означает также, что R2=R3, а R1=R4. Тогда величина Х будет равна

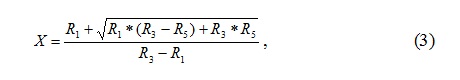
Аэродинамическое сопротивление всего диагонального соединения можно определить, используя величины сопротивлений любой пары ветвей – R1 и R2 или R3 и R4

Понятие аэродинамической симметрии в данном случае означает парное равенство сопротивлений для определяющих ветвей диагонального соединения – R1=R4 и R2=R3.

Вышеописанную закономерность (3,4) можно считать частным случаем, однако существует и общая закономерность, характеризующая аэродинамическую симметрию любого диагонального соединения. Она проявляется в том, что диагональное соединение можно трансформировать, как минимум, еще в одно соединение с таким же сопротивлением (рис.2).

Так, если известны сопротивления всех ветвей диагонального соединения (см. рис.1), то, соответственно, новые сопротивления ветвей диагонального соединения (Rа, Rб, Rс, Rе)

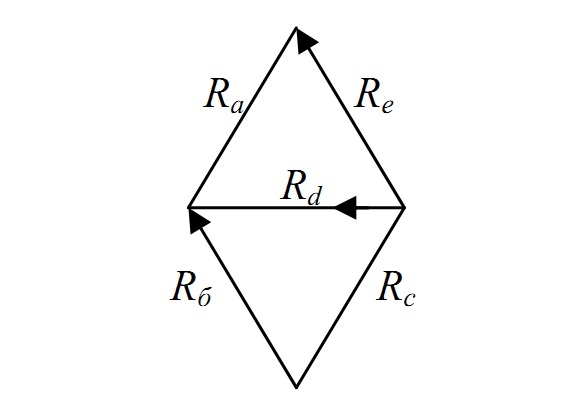
Рис. 2 – Схема движения воздуха в диагональном соединении определяются из следующих соотношений (сопротивление ветви-диагонали не изменяется):

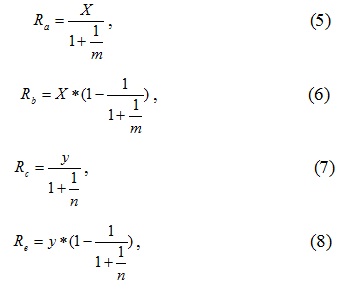
где X – сумма сопротивлений ветвей R1 и R2;
m – отношение сопротивлений R4 к R3;
у – сумма сопротивлений вервей R3 и R4;
n – отношение сопротивлений R2 к R1.

Таким образом, одно и тоже диагональное соединение имеет, как минимум, два набора сопротивлений для четырех определяющих ветвей (при неизменном сопротивлении ветви-диагонали), при котором общее сопротивление диагонального соединения остается неизменным. Одним из признаков этого является то, что сумма сопротивлений ветвей диагонального соединения до трансформации и после нее, не изменяется

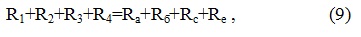
Все вышеприведенное позволяет считать, что использование известных закономерностей, описывающих распределение воздуха в параллельных соединениях, позволяет формировать диагональные соединения с заранее заданными аэродинамическими параметрами.

Другими словами, задаваясь величиной сопротивления всего диагонального соединения можно формировать необходимое соотношение расходов воздуха (газа или жидкости) в его отдельных ветвях.


Библиографический список