Автор: А.И. Федоренко
Эффективность и безопасность отработки месторождений подземным способом во многом зависит от характера и величины горного давления, а также от принятого метода управления им. Поскольку скальные горные породы по своим свойствам могут рассматриваться как упругие тела, при образовании в их массиве любой выемки происходит перераспределение напряжений вокруг нее, а следовательно, происходит изменение напряженно-деформированного состояния массива, особенно в его приконтурной части. Форма проявления горного давления может быть различной и зависит в основном от свойств горного массива, величины и характера изменения напряженного состояния. Большую роль играет исходное напряженно-дефор-мированное состояние нетронутого массива. Зная напряженное состояние массива и его физико-механические свойства можно производить оценку проявления горного давления в удароопасных условиях в том или ином подземном сооружении.
В настоящее время очистные работы ведутся на глубине 600-750 м от уровня земной поверхности, подготовительные достигают 850-900 м и неуклонно понижаются. С глубиной происходит рост исходного поля напряжений горного массива. Проходка выработок, отработка рудных блоков вызывают дополнительную концентрацию напряжений в отдельных частях массива, напряжения здесь могут в несколько раз превышать исходные значения. Их уровень сопоставим с пределами прочности горных пород на разрушение и поэтому при отработке блоков в рудном и вмещающем массивах регистрируется большое количество динамических проявлений горного давления в виде заколообразований,стреляний, толчков [1]. Глубокие рудники характеризуются значительным ухудшением горно-геологических условий и переходом горного массива в предельно-напряженное состояние. Это ведет к пересмотру положений по управлению состоянием приконтурного массива. Ведутся интенсивные исследования в вопросах крепления горных выработок путем использования самого массива горных пород в качестве крепежного материала в сочетании с анкерами, решетчатой затяжкой набрызгбетоном и т.д. Однако, до настоящего времени недостаточно изученными остаются вопросы взаимодействия горных пород, окружающих выработанное пространство с элементами крепей в удароопасных условиях, методы управления состоянием массива.
На наш взгляд существенную роль в управлении состоянием массива горных пород, окружающих выработку, играют роль горные породы, оснащенные анкерами, установленными особым образом.

Однако, теоретического обоснования расположения анкеров в массиве в литературных источниках практически не встречается. Поэтому за основу были приняты исследования, выполненные в работе [2], на основании которых композиционные материалы с однонаправленным армированием обладают высокими механическими характеристиками только при нагружении вдоль армирования. При нагружении поперек армирования и при сдвиге жесткость и особенно прочность материала оказываются весьма низкими, так как они определяются свойствами матрицы. В связи с этим однонаправленные материалы в чистом виде практически не используются в конструкциях.
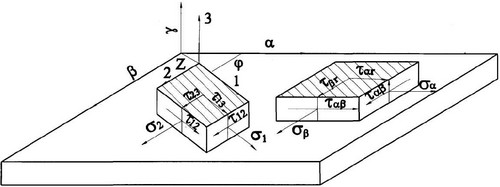
Рассмотрим слой, отнесенный к координатам 1, 2, 3 связанным с направлением армирования (рис. 1).
В однонаправленном материале ось 1 совместима с направлением армировния. Предположим, что элемент слоя находится в условиях плоского напряженного состояния. Поскольку оси координат 1, 2 являются осями ортотропии, закон Гука для слоя может быть записан в виде
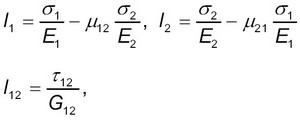 (1)
(1)где:
Е1, Е2 и G12 – модули упругости в направлениях 1, 2 и модуль сдвига в плоскости слоя; μ12, μ21 , – коэффициенты Пуассона.
Из выражения (1) определим напряжения
 (2)
(2)
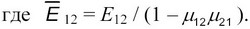
Здесь имеет место условие симметрии упругих постоянных
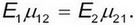 (3)
(3)Введем ортогональные координаты α, β, γ и предположим, что ось 1 армированного слоя составляет с осью α угол φ (рис.1).
Статические соотношения, связывающие напряжения в системах координат α, β и 1, 2 следующие:
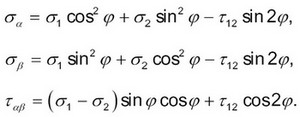 (4)
(4)Геометрические соотношения, позволяющие выразить деформации в системе координат 1,2 через деформации в осях α, β, можно записать следующим образом [3]
 (5)
(5)Получим теперь соотношения, связывающие напряжения σα, σβ, τα β с деформациями lα, lβ, lαβ. С этой целью подставим деформации l1, l2, l12 в закон Гука (2), а полученные в результате этой подстановки напряжения σ1, σ2, τ12 в соотношения (4). После некоторых преобразований с помощью условия симметрии (3) запишем физические соотношения для слоя, армированного под углом φ к оси α:
 (6)
(6)
Для получения обратных соотношений можно разрешить уравнение (6) от- носительно деформаций. Однако проще повторить их вывод, используя статические и геометрические соотношения, обратные (4) и (5). Разрешая (4) относительно напряжений σ1, σ2, τ12 и (5) относительно lα, lβ, lαβ имеем:
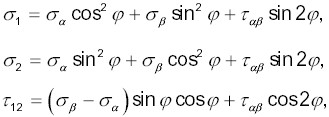 (8)
(8) (9)
(9)Равенство (8) может быть получено, если сложить первое соотношение (4) умноженное на cos2 φ, второе - умноженное на sin 2 2φ Остальные выводятся аналогичным образом. Подставляя теперь напряжения σ1, σ2, τ12 (8) в Закон Гука (1), а полученные таким образом деформации l1, l2, l3 - в правые части равенства (9), запишем выражения, обратные (4)
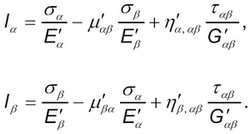 (10)
(10)где:
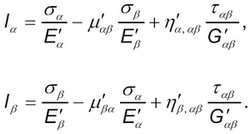
где:
где Eα ', Eβ ', Gαβ – модули упругости слоя в направлении α и β и модуль сдвига в плоскости армирования в этих осях; μ'α β μ'β α – коэффициенты Пуассона; η– коэффициенты, определяющие влияние касательных напряжений на удлинение и нормальных напряжений на деформацию сдвига. Наличие этих коэффициентов показывает, что слой, ортотропный в координатах 1, 2, является анизотропным в координатах α, β.
На основе изложенного примем, что x = 0,01. Это объемное содержание анкеров в породе; x1 = 0,3 - доля вертикальных анкеров, установленных в приконтурном массиве; x2 = 0,5 (1 – x1) – доля наклонных анкеров второго семейства; x3 = 1 – x1 – x2 – доля наклонных анкеров третьего семейства; E=2∙105 МПа – модуль упругости породы, МПа; G = 1000 МПа – модуль сдвига породы с трещинами; μ=0.25 - коэффициент Пуассона; E1=E∙x+En(1-x) - породный модуль упругости породы с анкерами. Деформации на единицу напряжения равны:
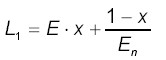 (12)
(12)Деформация массива с анкерами при cдвиге на единицу напряжения равна:
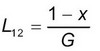 (13)
(13)Поперечный модуль упругости поперек анкеров равен:
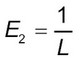 (14)
(14)Модуль сдвига в осях 1,2 G12=1 / L12
Деформация массива с анкерами, расположенными под углом α на основе выражения (11) равна:
 (15)
(15)Модуль упругости массива с анкерами, расположенными под углом α равен:
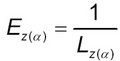 (16)
(16)Деформация массива с анкерами, расположенными под углом α равна:
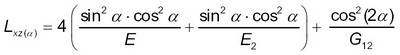 (17)
(17)Модуль сдвига массива с анкерами, расположенными под углом α в осях x, z равен:
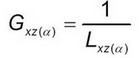 (18)
(18)Модуль упругости массива, оснащенного анкерами всех семейств равен:
 (19)
(19)Модуль сдвига массива, оснащенного анкерами всех семейств равен:
 (20)
(20)Модуль сдвига для всех семейств во второй плоскости равен:
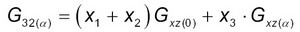 (21)
(21)Угол расположения анкеров в массиве приведен в радианах и изменяется от 0 до 1°.
На основании выполненных расчетов установлено, что по сравнению с вертикальным расположением анкеров
наклонное расположение под углом 45° увеличивает несущую способность массива до 16 %. Однако, с технической точки зрения устанавливать анкера следует под углом 50-60° и даже в
этом случае устойчивость системы порода-крепь
будет выше более чем на 10 %. Для повышения несущей способности кровли выработок особенно в удароопасных условиях целесообразно применять трубчатые анкеры взрывного закрепления, которые в процессе взрывной установки уменьшают напряжения в кровле выработок. Кроме того, шпуры с установленными в них трубчатыми анкерами остаются полыми (свободными), что способствуют разгрузке массива постоянно.
В породах третьей и четвертой категорий устойчивости целесообразно на анкеры навешивать сетку и на кровлю выработки наносить набрызгбетон регулируемой толщины в зависимости от состояния массива. Таким образом, использование горных пород как прочного заполнителя крепи в сочетании с анкерами, расположенными особым образом, сеткой и набрызгбетоном создают в кровле выработки замкнутую устойчивую систему, способную работать в широком диапазоне горно-геологических условий.