Учет рисков в сетевом планировании развития горных работ при отработке выемочного участка угольной шахты

Авторы: В.В. Назимко, д.т.н., профессор, И.В. Назимко, к.т.н., доцент, Донецкий национальный технический университет А.А. Яйцов,

Источник: Національна бібліотека України імені В.І. Вернадського, Київ [элетронный ресурс]. – Режим доступа: http://www.nbuv.gov.ua

Планирование развития горных работ связано с высоким уровнем рисков. Риски связаны с неопределенностью горно-геологических условий отработки запасов полезного ископаемого, ценовой политики, неустойчивостью экономики, уровнем надежности горнодобывающей техники, человеческим фактором и т. д. Указанные риски существенно усложняют решение задач сетевого планирования. Последнее время интенсивно развивается новое научное направление в экономике и технике, связанное с количественной оценкой рисков, обусловленных неопределенностями геологической природы , экономической ситуации и другими факторами [1-9]. Это дает возможность повысить надежность планирования и снизить сроки реализации проектов, а также обеспечить гарантийную окупаемость инвестиций, социальных и политических условий, в которых реализуется проект.

Целью данной работы является разработка и апробация модели сетевого планирования с учетом неопределенности экономических, природных условий.

В данной статье описаны результаты математического моделирования рисков, которые возникают при сетевом планировании развития горных работ. Компьютерная система оценки рисков основана на пакете компьютерных программ, которые позволяют выполнить детальный статистический анализ исходной горно-геологической, горнотехнической и экономической ситуации, характерной для конкретного выемочного участка или шахты (рис. 1). На основе такого анализа устанавливают законы распределения входных параметров. Например, известно, что предел прочности горных пород на одноосное сжатие распределяется согласно логнормальному закону [10].

Величина износа (или остаточный ресурс) крепи очистного забоя распределена крайне неравномерно и обычно не противоречит распределению Вейбула [11]. Распределения могут иметь любую форму и модальность. Так, в известном пакете [6] используется 38 распределений. Следует отметить, что в подавляющем числе реальных ситуаций входные величины не являются детерминированными, а заменяются распределениями того или иного вида , закон которого устанавливается в процессе предварительного анализа исходных данных. При этом не обязательно все данные анализировать экспериментально. Часть распределений можно построить на основе экспертных оценок или на основании известных закономерностей, примеры которых цитировались выше для распределения прочности пород и ресурса крепей очистного забоя.

Подавляющее число производственных процессов неразрывно связано с экономической и политической ситуацией. Поэтому одной из важнейших групп исходных данных являются экономические показатели и социальные параметры среды , в которой производственный процесс протекает. Именно поэтому необходим анализ экономических показателей и социальной ситуации.

Второй блок системы оценки рисков содержит построение модели исследуемого процесса. В данной статье будет анализироваться процесс подготовки и отработки выемочного столба на угольной шахте, однако данная система применима для анализа рисков в любых процессах. Так, возможен анализ риска потери устойчивости горной выработки по анализу бифуркации кластерной мозаики массива горных пород [12].

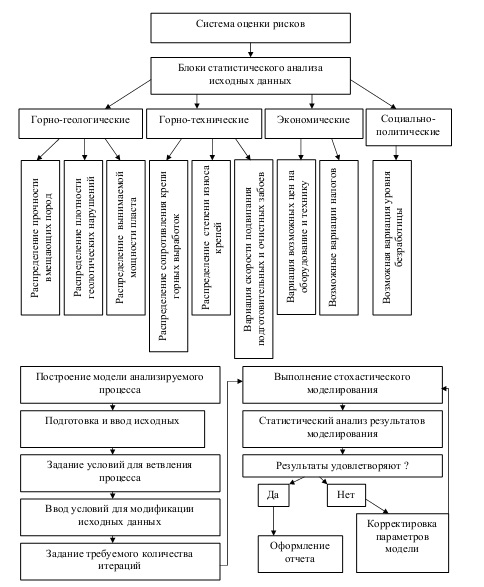
Рисунок 1. Блок-схема стохастического моделирования риска

Процесс подготовки и отработки выемочного участка наиболее удобно описать с помощью сетевой модели [13]. Такая модель строится на основе графа, в котором события связаны между собой во времени в определенной последовательности . Например, подготовка выемочных штреков происходит между моментами времени 1 и 3 и длится в среднем 4 месяца (рис. 2). Параллельно производится закупка и доставка горнодобывающего оборудования (механизированного комплекса, конвейеров, вентиляторов и т. д.), что планируется выполнить в среднем за 1 месяц (вектор 1 между моментами времени 1 и 2 на рис. 2).

Только после этого можно проводить монтажную камеру (стрелка между моментами времени 2 и 4) и монтировать очистной комплекс ( стрелка между моментами времени 4 и 7).

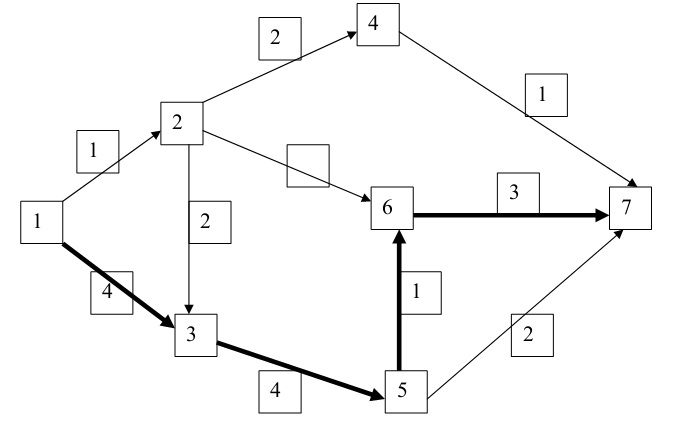
Рисунок 2. Упрощенный сетевой граф планирования подготовки и отработки выемочного участка

Параллельно планируется сооружение системы дегазации, транспорта и других технологических процессов, которые необходимо для отработки выемочного участка. Важно подчеркнуть, что длительность отдельных операций заранее неизвестна и можно предположить только наиболее вероятное значение длительности процесса, а также указать диапазоны его разброса в меньшую и большую стороны (не обязательно одинаково), а также указать закон распределения возможных величин длительности процесса. Отсюда возникает неоднозначность результатов планирования, причем величина этой неоднозначности может быть выражена степенью риска [2-6].

Под риском в данной статье понимается степень неопределенности возможных исходов планируемого процесса в будущем. Для того чтобы выразить количественно степень риска, отметим его основные характеристики. Риск может быть объективен или субъективен. Так при бросании монеты риск выпадения орла или решки объективен и зависит от физических законов тяготения и динамики. Даже, несмотря на то, что результат бросания монеты заранее неизвестен, степень риска может быть определена совершенно точно, исходя из предыдущего опыта и здравого смысла.

Предсказание погоды на завтра носит явно выраженный субъективный риск, поскольку на основании одной и той же исходной информации, компьютеров и программ специалист А может дать вероятность дождя в пределах 30 %, а синоптик В определит ее на уровне 50 %. Оба специалиста будут правы, и для описания субъективного риска разработана теория нечетких множеств, которая оперирует такими субъективными параметрами, как «завтра может быть дождь» или «завтра, скорее всего, будет дождь» и т. п . [14]. Важно, что прогноз субъективного риска остается открытым и его вероятность может быть всегда уточнена на основе дополнительной информации.

В большинстве реальных случаев риск является субъективным, и это является главной причиной сложностей, которые возникают при попытках количественной оценки степени субъективного риска. Так при ставке выигрыша 1 гривны в случае выпадения решки и проигрыша 1 гривны при выпадении орла большинство людей пренебрегут риском проигрыша в игре. Если же ставки поднимутся до +1000 и -1000 гривен, большинство людей сочтут такую игру рискованной. Однако найдется небольшое количество людей, которые пренебрегут риском и при повышенном уровне ставок.

Наконец, мы всегда имеем возможность избежать риска или принять его сознательно. Существуют персональные предпочтения для принятия или уклонения от риска.

В нашей задаче будет оцениваться реалистичная длительность проекта, который состоит в подготовке и отработке выемочного столба . Для того чтобы дать количественную оценку риска, мы должны определить возможные значения ключевого параметра процесса (в данном случае длительности проекта подготовки и отработки выемочного столба ) и оценить вероятность каждого из возможных зна- чений. Теоретически можно использовать теорию вероятности и математическую статистику для вычисления указанных параметров . Однако в подавляющем числе реальных ситуаций вывод формул становится настолько громоздким и трудоемким, что такую задачу можно решить только численным методом. Лишь при совокупном действии независимых событий дисперсия погрешности определения определенной величины вычисляется относительно просто, и то необходимо знать частные производные распределений ошибок по всем влияющим факторам [15]. Если исследуемый процесс описывается совокупностью условных вероятностей, тогда строгое решение задачи в формулах становится практически невозможным. Именно поэтому задача любой сложности решается достаточно просто численным методом стохастического моделирования.

Вначале строится модель процесса, в данном случае сетевой граф процесса подготовки и отработки выемочного столба (рис. 2). Затем подготавливаются и вводятся исходные данные. В качестве исходных данных в данном случае используются такие параметры, как средняя длительность отдельных процессов, их диапазон разброса в меньшую и большую сторону и закон распределения. Точно такие же законы распределения задаются для прочности вмещающих пород , степени износа оборудования и т. д. Основная масса исходной информации вводится по результатам анализа исход- ных данных, которые изображены блок-схемой на верхней части рис. 1.

Затем задаются условия ветвления процесса. Например, при уровне безработицы свыше 10 % проходка выемочных штреков планируется собственными силами, а в противном случае подрядчиками. Соответственно используются разные сроки выполнения данной операции и ее стоимость.

Вводится также информация для модификации исходных условий. Например, средняя продолжительность и диапазон разброса сроков проходки выемочных штреков будет уменьшаться обратно пропорционально ценам на уголь. Затем задается требуемое количество итераций и начинается стохастическое моделирование. Технически такой процесс выполняется компьютером так, что выполняется решение одной и той же задачи определенное число раз, равное количеству итераций. Однако при каждом решении исходные данные с помощью генератора случайных чисел выбираются из возможного диапазона, заданного исходными распределениями. В результате на выходе получаем не одну величину искомого параметра, например, срока завершения проекта, а распределение возможных сроков.

В таблице 1 приведено описание исходных данных, используемых в демонстрационном примере процесса , сетевой граф которого изображен на рис. 2. В первых двух столбцах задается топология графа (откуда и куда направлен вектор процесса). В третьем столбце задана длительность процесса в месяцах. Для упрощения программы длительность задается в целых числах, например в сутках , часах, сменах и т. п .

Таблица 1. Описание исходных данных

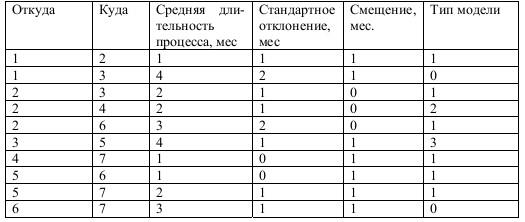
В четвертом столбце задано стандартное отклонение распределения длительности каждого элементарного процесса , а в столбце пятом смещение для несимметричных распределений. В последнем столбце обозначается тип модели распределения, где 0 обозначает равномерное распределение, 1 – нормальное, 2 – логнормальное, 3 – Вейбула. При задании нулевого стандартного отклонения в конкретном элементарном процессе стохастичность отсутствует , то есть процесс становится абсолютно детерминированным. Полезно начать моделирование с одной итерации , в которой все входы являются детерминированными. Это дает возможность сопоставить результаты детерминированного и стохастического моделирования. Наглядно это сопоставление на планограмме работ, на которой наносятся графики самого раннего начала и самого позднего завершения каждой работы, их моды и / или медианы , а также процент времени , который конкретная работа пребывает на критическом пути.

Решение для детерминированного варианта приведено в таблице 2. В столбцах 1, 2, 3 приведены топология графа и средняя длительность элементарных процессов. Далее в столбцах 4 и 5 приведены самый ранний и самый поздний сроки начала, а в столбцах 6 и 7 самые ранние и поздние сроки завершения процессов. В столбцах под номерами 8 и 9 приведены полный и свободный резервы времени, по которым определен критический путь графа 1-3-5-6-7. Этот путь отмечен жирными стрелками на рис. 2.

Результаты стохастического моделирования не столь лаконичны и были обработаны с помощью статистических пакетов. В данном примере при проведении стохастического моделирования использовано 100 итераций.

На рис. 3, а показано равномерное распределение возможных длительностей элементарного процесса 6-7. Такое распределение было задано в качестве исходного в данном звене сети (см. табл . 1).

С учетом всех исходных данных были получены результирующие распределения искомых параметров сети. Прежде всего, заметим , что все параметры распределены неравномерно . В данном звене сети самый ранний срок начала процесса 6-7 изменяется от 8 до 12 месяцев, причем наиболее вероятное начало смещено в правую сторону и совпадает примерно с 11 месяцами (рис. 3, б).

Самый поздний срок начала (а) и самый ранний срок завершения (б) процесса 6-7 распределены так, что более вероятные величины размещены в левой части распределения (рис. 4) Наоборот, самый поздний срок завершения проекта распределен с предпочтением сроков в правую сторону ( рис. 5). На отдельных распределениях можно обнаружить многомодальность, которую, тем не менее, следует проверить дополнительным количеством итераций.

Важно, что теперь критический путь сети не является детерминированным. В зависимости от случая, выпадают такие пути, как 1-2-3-5-6-7, 1-2-3-5-7 и другие, что свидетельствует о неопределенности возможных реализаций всего технологического процесса. Вероятность реализации отдельных вариантов определяется с помощью распределений, примеры которых приведены на рис. 3-5. При этом субъективность оценки степени риска минимизируется. Элемент субъективности вносится только на конечном этапе анализа всего процесса стохастического моделирования, когда специалисты-эксперты принимают решение о приемлемости проекта или необходимости его модификации, поскольку риск неблагоприятных исходов очень велик с учетом всех возможностей шахты и социально-экономической ситуации.

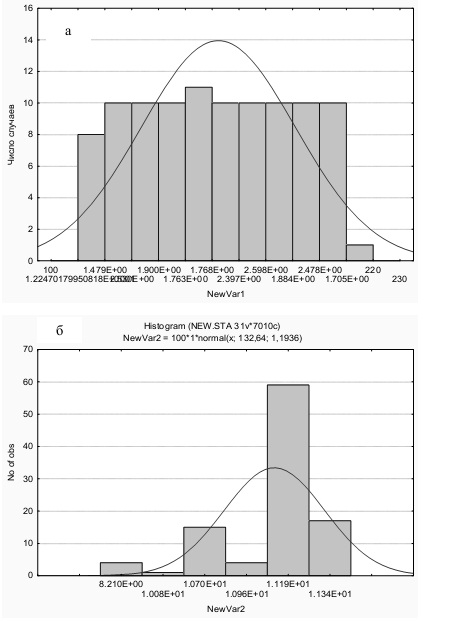
Рисунок 3. Распределение длительности процесса 6-7 (а) и самого раннего срока его начала (б)

Таблица 2. Результаты моделирования детерминированного варианта

Надежность принятия успешного варианта усиливается возможностями детального анализа результатов стохастического моделирования. На рис. 6 показан пример анализа корреляционной связи между самым ранним сроком начала процесса 6-7 и самым ранним сроком его завершения. Видно, что такая связь существует и выражается экспоненциальной зависимостью. Эллипсом очерчены точки, вошедшие в 95 % доверительный интервал оценок. Возможности оптимизации сетевой модели существенно расширяются благодаря использованию таких продвинутых методов математической статистики, как проверка чувствительности модели к входным факторам с помощью ранговой корреляции Спирмана, методов six sigma и др. [2-4].

В рассматриваемой в данной статье модели встроен алгоритм оптимизатора, базирующийся на генетическом алгоритме. Этот алгоритм позволяет достаточно быстро и надежно находить среди огромного количества возможных вариантов реализации проекта такой , срок или экономические показатели которого минимальны при заранее заданных граничных условиях.

В настоящее время разработанная система используется на шахте Красноармейская-Западная № 1 при совершенствовании проекта отработки выемочного участка 4 южной лавы блока 10. При этом благодаря стохастическому моделированию удалось избежать возможных неблагоприятных исходов, когда сроки подготовки и отработки запасов могли превысит плановые в 2,2 раза, что привело бы к потере годовой добычи в размере 34 % от плановой.

Разработанная система является эффективным инструментом планирования горных работ в сложных современных рыночных условиях и кризисной ситуации. Такая система может быть использована при планировании инвестиционных проектов , строительства, разработки месторождений полезных ископаемых . Модель позволяет в 1,5 – 2,2 раза уменьшить сроки строительства и отдачи от вложенных инвестиций, а также повысить прибыль на 25 – 50 % от реализации планируемых проектов. В дальнейшем предусматривается проверка и апробация разработанной системы при строительстве очистных сооружений, оценка эффективности и надежности планов ликвидации аварий, освоения новых технологий добычи газа при разработке угольных месторождений.

Рисунок 4. Распределение самого позднего срока начала (а) и самого раннего срока завершения (б) процесса 6-7

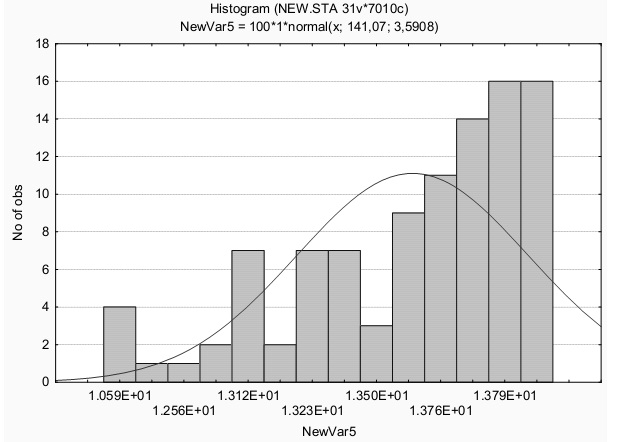
Рисунок 5. Распределение самого позднего срока завершения процесса 6-7

Рисунок 6. Корреляция между самым ранним сроком начала процесса 6-7 и самым ранним сроком его завершения

Литература

1. Herz D.B., Thomas H. Practical Risk Analysis – An Approach Through Case Histories. – New York: John Wiley and Sons, 1984. – 562 p.
2. James A.M. Decisions Involving Uncertainity: An @RISK Tutorial for the Petroleum Industry. – Newfield: Palisade Corp, 2000. – 347 p.
3. Nersesian R.L. @RISK Bank Credit. – Newfield: Palisade Corp, 2001. – 428 p.
4. Newendrop P.D., Schuyler J. Decision Analysis for Petroleum Exploration, 2nd Ed. – Aurora: Planning Press, 2000. – 395 p.
5. Pouliquen L.Y. Risk Analysis in Project Appraisal // World Bank Staff Occasional Papers. – Baltimore: John Hopkins Press, #11, 1970. – pp. 156-158.
6. Winston W. Financial Models Using Simulation and Optimization. – Newfield: Palisade Corp, 2000. – 265 p.
7. Winston W., Albright C. Practical Management Science. Thomson Learning, 2000. – 312 p.
8. Winston W. Spreadsheet Modeling Using@RISK. Thomson Learning, 2000. – 372 p.
9. Хобта В. М. Формирование хозяйственных решений. – Донецк: Каштан, 2003. – 416 с.
10. Шашенко А.Н., Сдвижкова Е.Н., Кужель С.В. Масшатбный эффект в горных породах. – Днепропетровск: НГУ, 2005. – 146 с.
11. Назимко В.В., Красько А.Н. Учет неопределенности при оценке устойчивости непосредственной кровли в действующем очистном забое // Проблемы горного давления. – Донецк: ДонНТУ, вып. 9, 2003. – С. 45–67.
12. Бокий Б.В., Александров С.Н., Назимко И. В. Кластерный механизм динамики сдвижения подрабатываемого движущейся лавой массива горных пород // Матеріали міжнародної конференції «Форум гірників». – Дніпропетровськ : Національний гірничий університет, 2007. – С .55–59.
13. Петрова Л. Г. Введение в сетевое планирование. – Новосибирск: НГУ, 1969. – 214 с.
14. Zadeh L. The role of fuzzy logic in the management of uncertainty in expert systems. Gupta M., Kandel A., Bandler W. // Approximate Reasoning in Expert Systems. – North Holland. – 1985. – 538 p.
15. Афири А., Эйзен С . Статистический анализационный подход с использованием ЭВМ. М .: – Мир, 1982. – 488 с.