ПСЕВДООБРАЩЕНИЕ МАТРИЦЫ НОРМАЛЬНЫХ УРАВНЕНИЙ СВОБОДНЫХ ГЕОДЕЗИЧЕСКИХ СЕТЕЙ
Автор: Профессор, доктор техн. наук В.Н. Ганьшин.
Источник: Известия вузов. Геодезия и аэрофотосъемка. – 1989, вып. 6. – с. 3-5.
Автор: Профессор, доктор техн. наук В.Н. Ганьшин.
Источник: Известия вузов. Геодезия и аэрофотосъемка. – 1989, вып. 6. – с. 3-5.
В статье предлагается псевдообращение матрицы  нормальной системы уравнений свободной сети, имеющей дефект, равный размерности l (практически
нормальной системы уравнений свободной сети, имеющей дефект, равный размерности l (практически 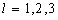 с помощью стандартных матриц
с помощью стандартных матриц 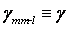 (прием этот предложен в книге [1]). Используя полученный результат, вычисление матрицы
(прием этот предложен в книге [1]). Используя полученный результат, вычисление матрицы 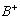 можно свести к суммированию четырех матриц.
можно свести к суммированию четырех матриц.
Пусть  - неособенная матрица размерами
- неособенная матрица размерами 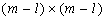 , получаемая из матрицы В вычеркиванием в ней l строчек и l столбцов, относящихся к некоторому произвольному пункту сети. Для определенности и удобства записи будем считать, что таким пунктом является последний
, получаемая из матрицы В вычеркиванием в ней l строчек и l столбцов, относящихся к некоторому произвольному пункту сети. Для определенности и удобства записи будем считать, что таким пунктом является последний 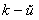 , где
, где 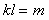 ; ранг матрицы В обозначим
; ранг матрицы В обозначим 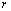 , т.е.
, т.е. 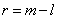 .
.
Известно [2;3;1], что матрица 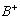 , псевдообратная по отношению к матрице В, представляется произведением
, псевдообратная по отношению к матрице В, представляется произведением
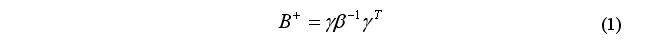
Где 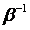 - матрица обратная по отношению к матрице
- матрица обратная по отношению к матрице  .
.
В работе [1] дано правило написания матрицы  для любого
для любого  и
и 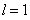 . Обобщая это правило на случай произвольного значения l, в блочной записи получаем для
. Обобщая это правило на случай произвольного значения l, в блочной записи получаем для 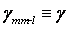 следующее значение:
следующее значение:
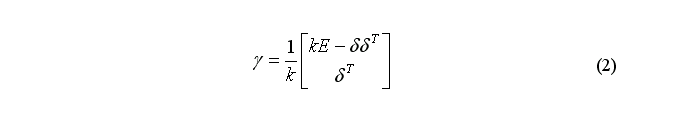
Где 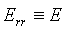 - единичная матрица размером
- единичная матрица размером 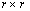 ;
;
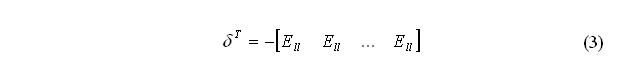
Т.е. блочная матрица 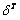 содержит
содержит 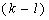 единичных блоков размерами
единичных блоков размерами 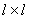 ;
;
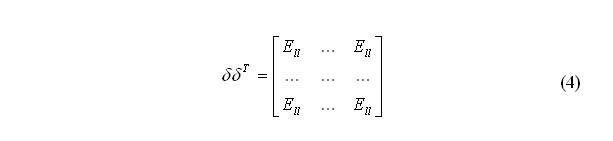
Так, применительно к случаю 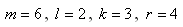 получим
получим
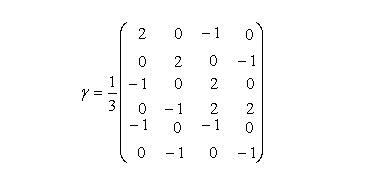
Подчеркнем, что матрица 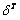 находится на месте вычеркнутых l строчек (в данном случае, принадлежащих данному пункту).
находится на месте вычеркнутых l строчек (в данном случае, принадлежащих данному пункту).
Произведение, стоящее в правой части выражения (1), может быть представлено в виде алгебраической суммы четырех матриц
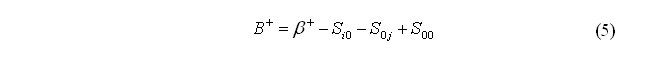
Где три последних матрицы являются производными от первой.
Матрица 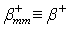 получается из матрицы
получается из матрицы 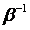 добавлением в ней l строчек и l столбцов (на места, соответствующие строкам и столбцам вычеркнутым в матрице В), все элементы которых нули. В нашем примере были вычеркнуты строки и столбцы, соответствующие последнему пункту, поэтому матрицу
добавлением в ней l строчек и l столбцов (на места, соответствующие строкам и столбцам вычеркнутым в матрице В), все элементы которых нули. В нашем примере были вычеркнуты строки и столбцы, соответствующие последнему пункту, поэтому матрицу 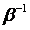 для перехода к матрице
для перехода к матрице 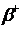 надлежит окаймить l строками и l столбцами с нулевыми элементами.
надлежит окаймить l строками и l столбцами с нулевыми элементами.
Матрицу 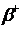 разобьем на блоки размерами
разобьем на блоки размерами 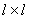 , которые будт содержать элементы, находящиеся на пересечении строчек
, которые будт содержать элементы, находящиеся на пересечении строчек 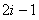 и
и 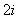 (соответствующие
(соответствующие 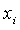 и
и  ) и столбцами
) и столбцами 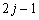 и
и  (соответствующие
(соответствующие 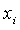 и
и  ), где
), где 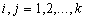 .
.
Так в случае 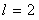 , образованный нами блок будет иметь вид
, образованный нами блок будет иметь вид
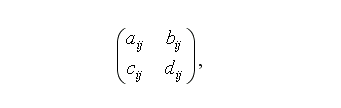
Где 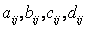 - соответствующие элементы матрицы
- соответствующие элементы матрицы 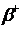 (в нашем примере последние блоки будут нулевыми).
(в нашем примере последние блоки будут нулевыми).
Аналогичным образом на блоки разбиваются и матрицы 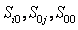 . Эти блоки соответственно будут:
. Эти блоки соответственно будут:

Где

И т.д. (для c и d).
Переход от элементов матрицы 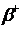 к элементам матрицы
к элементам матрицы 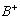 сводится к последовательному «осереднению» элементов блоков матрицы
сводится к последовательному «осереднению» элементов блоков матрицы 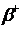 сначала по строкам, затем – по столбцам и, наконец, по совокупности всех одноименных элементов в блоках матрицы
сначала по строкам, затем – по столбцам и, наконец, по совокупности всех одноименных элементов в блоках матрицы 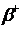 .
.
В заключении подчеркнем, что обосновать верность формулы (5) можно непосредственно, исходя из условий, связывающих матрицы В и 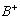 , - правая часть выражения (5) удовлетворяет всем этим условиям.
, - правая часть выражения (5) удовлетворяет всем этим условиям.
1. Ганьшин В.Н., Стороженко А.Ф., Ильин А.Г., Буденков Н.А., Цюнько В.И. Измерение вертикальных смещений сооружений и анализ устойчивости реперов. М.: Недра, 1981, 216с.
2. Гантмахер Ф.Р. Теория матриц. М.: Наука, 1967, 576с.
3. Альберт А. Регрессия, псевдообращение и рекуррентное оценивание. М:. Наука, 1977, 223 с.