Картавенков И.Г. - О методике построения равноточных нуль-свободных нивелирных сетей

Предпосылки

При анализе точности геодезических измерений и их функций они делятся на неравноточные и равноточные. Последние являются частным случаем первых, а для их характеристики пользуются весами. В практике эмпирические веса достаточно вычислять с двумя значащими цифрами, а в отдельных случаях с двумя десятичными знаками, исходя из известной зависимости 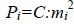, где - средняя квадратическая погрешность (ошибка), так как она определяется не надежно. Если в геодезической (нивелирной) сети, кроме необходимых (t), в ней есть избыточные величины (r), то все измеренные величины (n) подлежат уравниванию под известным условием метода наименьших квадратов При этом составляется и решается система нормальных уравнений, которая в параметрическом способе уравнивания имеет вид:

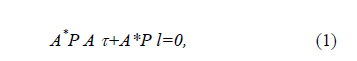
а вектор неизвестных поправок в выбранные параметры (отметки реперов) будет:

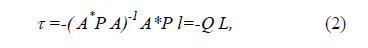
где элементы обратной матрицы коэффициентов системы нормальных уравнений, играющие роль обратных весов, в развернутом виде представляются матрицей

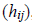Кроме отмеченного, последнее выражение позволяет выполнить оценку точности отметок и превышений , вычислить коэффициенты корреляции между ними , а также среднее значение средней квадратической ошибки отметки всех реперов вместе взятых (N), входящих в нивелирную сеть, по известным формулам:

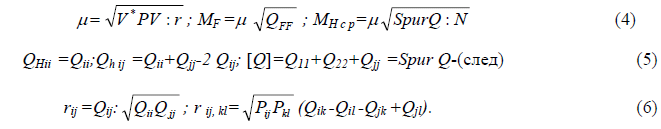
Приведенные формулы справедливы как для свободных (с одним исходным репером), так и для несвободных нивелирных сетей и ходов. Уравнивание превышений в нуль-свободных нивелирных сетях имеет особенность, когда превышения являются разностями отметок. Значения отметок при отсутствии исходных высот однозначно определить невозможно, так как решение приводит к вырожденной квадратной матрице 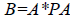, а поэтому требуются использования обобщенных обратных (псевдообратных) матрицы 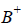, элементы 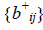которых играют такую же роль, что и обратные веса в формулах (3–6).

При уравнивании превышений в нуль-свободных нивелирных сетях под условием метода наименьших квадратов (или ) для получения единственного решения используется матрица 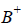и вводится дополнительное условие (требование) равенства нулю суммы уравненных отметок реперов 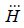(что равносильно условию 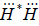[1]) или поправок :

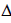где t — число реперов в сети; C — параметр, определяющий положение плоскости, относительно которой отсчитываются отметки.

Введение дополнительного условия соответствует реализации предположения о неизменности средней высоты (средней плоскости) реперов, однако порядок выбора параметра C в выражениях 7 и 8 (и связанное с ним положение плоскости) не определен. Поэтому получение элементов матрицы 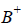будет иметь некоторую особенность по сравнению с получением их из выражения [1 и др.]:

где

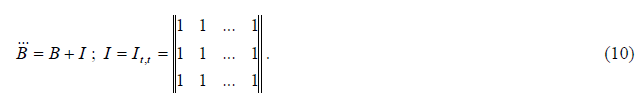
Если в 7 или 8 С не равно 1, то в выражении 9 при получении элементов 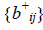следует вычитать сумму строки (столбца) матрицы 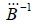в квадрате, умноженную на коэффициент С:

Выражение 9 реализовано в одной из программ профессора В.И. Мицкевича и используется для обоснования методики получения равноточной нуль-свободной нивелирной сети [3], а сделано это на примере сети с нашими дополнениями (рис. 1).

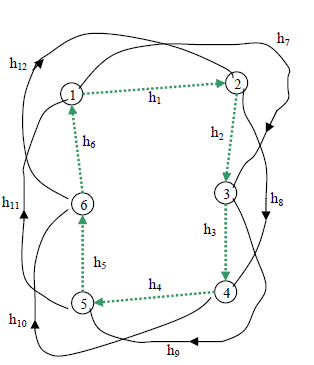
Рис. 1 - Замкнутый полигон и нивелирная сеть

В соответствии с выводами в работе Д.В. Усова [3] сеть считается равноточной, если (1) равны диагональные элементы матрицы 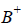или Q; (2) сеть является замкнутой; (3) исполненные измерения равноточны и уравнены под условием с дополнительным условием (7), соответствующим отсутствию в сети исходных пунктов. Сеть может иметь расположенные симметрично замыкающие. На рисунке видно, что, например, длины (число станций) звеньев 56 и 61 меньше длины (числа станций) замыкающей 51 примерно в два раза. Следовательно, чтобы замыкающая стала равноточной звену, измерения в ней должны выполняется два раза, что увеличивает объем работ. Если же предположить, что в замыкающей и звеньях превышения измеряются с одной установки прибора, то и в этом случае превышения будут, из-за разности плеч, измерены не совсем равноточно. Хотя, как известно, это мало отразится на конечных результатах.

Однако в ковариационной матрице, кроме диагональных элементов, имеются и недиагональные элементы, с помощью которых высчитывают величины обратных весов превышений (ошибки взаимного положения реперов), нормированную корреляционную матрицу отметок, а также коэффициенты корреляции между превышениями по известным формулам (5 и 6). Для их вычисления приведем данные [3] ( 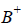), полученные для замкнутого полигона без замыкающих , но, учитывая симметричность матриц, запишем только их верхние треугольники.

Из приведенных матриц видно, что в каждой из них диагональные элементы равны, а поэтому каждая из них приводит к равноточному определению отметок, хотя след первой равен 1,09, а второй 2,92. Следовательно, в сети (рис. 1) точность определения отметок выше в 1,6 раза по сравнению с их точностью в замкнутом полигоне, но не прямо пропорциональна увеличению объема работ.

Используя численные значения элементов записанных матриц, вычислим по формуле (5) величины обратных весов уравненных превышений (взаимного положения определяемых реперов). При этом получим:

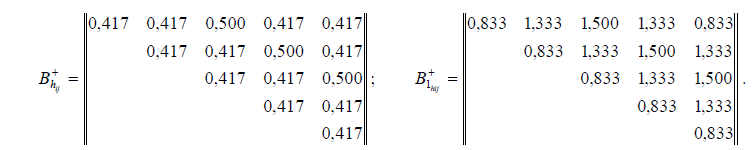
Таким образом, в сети с замыкающими веса соответствующих превышений равны 2,4 и 2,0, а в замкнутом полигоне они меньше и равны: 1,2, 0,75 и 0,67. Следовательно, по данному критерию рассматриваемые построения не являются равноточными.

Будут разными численные значения и коэффициентов корреляции между отметками 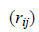в нормированной корреляционной матрице :

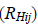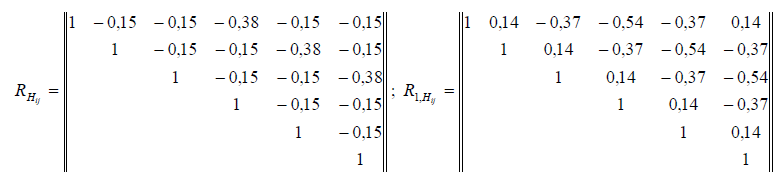
Неодинаковыми будут и коэффициенты корреляции между превышениями 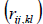. Например:

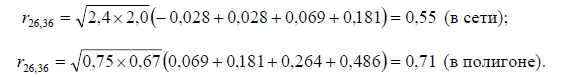
Далее приведем еще несколько их значений:

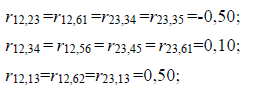
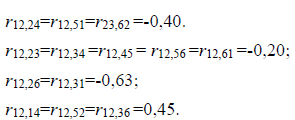
Представленные данные еще раз подтверждают, что каждое в отдельности рассматриваемое построение не является равноточным. Вместе с тем превышения в рассматриваемой сети можно уравнять шесть раз с одним из шести исходных реперов. Во всех шести случаях след обратной матрицы будет одинаков, как и квадратичная форма. Так, приняв за исходный репер 6, получим обратную матрицу Q коэффициентов системы нормальных уравнений и матрицу 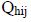обратных весов уравненных превышений (взаимного положения):

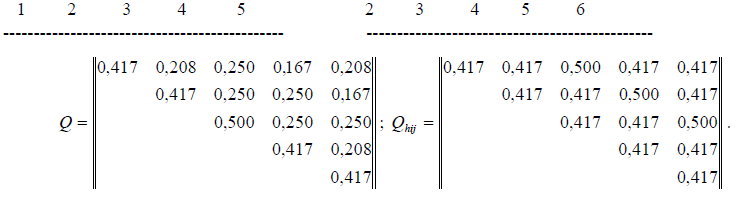
Сравнивания численные значения матриц и 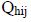, видим, что они одинаковы, а поэтому и веса превышений равны 2,4 и 2,0. Останутся одинаковыми и коэффициенты корреляции .

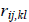В тоже время след матрицы Q=2,17, а матрицы 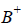=1,08. Таким образом, в рассматриваемом примере при уравнивании превышений в нуль-свободной сети произошло повышение (искажение) точности определяемых величин в 1,4 раза по сравнению с результатами в свободной сети, хотя средняя квадратическая ошибка единицы веса одинакова и конфигурация сети не изменялась. Вызвано это тем, что меняется начало отчета (система координат). В нуль-свободной сети оценка точности выполняется относительно средней плоскости и точки, являющейся центром тяжести лежащей на этой плоскости сети, в свободной — относительно точки совмещенной с исходным репером. Выбор дополнительного условия (средней плоскости) произволен [1]. Следовательно, в нуль-свободных сетях можно получать различные оценки, а это существенный недостаток упомянутых построений.

Примеры.

Приведем несколько простых построений, отвечающих требованиям нормативных документов [4, 5], когда «число реперов должно быть не менее трех», в которых погрешности определения отметок и уравненных превышений одинаковы при уравнивании измеренных величин как в нуль-свободной, так и в свободной сетях (рис. 2).

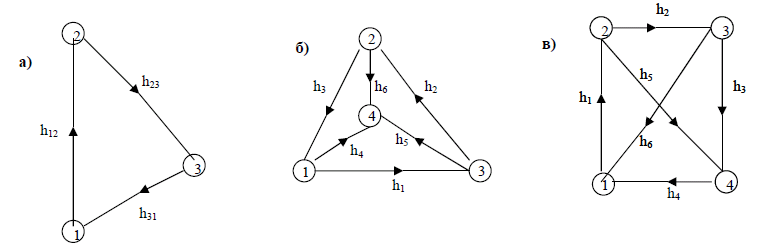
Рис. 2 - Построения без исходных пунктов

Первые два построения и их матрицы 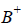заимствованы [1], а вычисление в этих построениях элементов матриц Q просто. Запишем (для рис. 2, а):

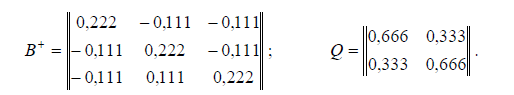
Из записанного видно, что 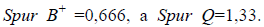Следовательно, в первом случае точность определения отметок в 1,4 раза выше, чем во втором. В это же время а 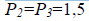и коэффициенты корреляции поменяли знаки Веса уравненных превышений в обоих случаях одинаковы — 1,5.

Для второго построения (рис. 2, б) запишем матрицы 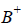и Q, приняв за исходный пункт 4:

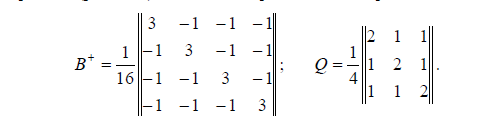
Из приведенного следует, что 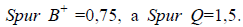Таким образом, в первом случае точность определения отметок в 1,4 раза выше, чем во втором. В это же время 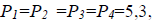а и коэффициенты корреляции поменяли не только знаки, но и величину 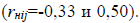Веса уравненных превышений в обоих случаях одинаковы 2,0, как и коэффициенты корреляции между уравненными превышениями:

Элементы матриц 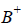и Q для построения 2, в совпадают с их значениями для построения (2, б), а поэтому не приводятся. Если же сравнить диагональные элементы матриц 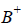соответствующие построениям (рис. 2, б и 2, в) с их значениями (рис. 1) (0,188 и 0,181), то видно, что точность определения отметок в них практически одинакова (расхождение весов не превышает 4%). Однако, последние построения более просты по исполнению и ближе к практике. Трудно представить граф сети (рис. 1), если добавить в нем еще дополнительно 18 замыкающих, как это может быть в соответствии с рекомендациями в работе Д.В. Усова [3]. Ведь "для нивелирной сети оптимальными и необходимыми измерениями (звеньями) будут те измерения, которые образуют дерево графа с наименьшим периметром" [6, с. 76].

Таким образом, рассмотренные три построения действительно равноточны, если каждое из них анализировать отдельно. Веса (величины обратных весов — диагональные элементы) в каждом построении одинаковы, а также одинаковы веса уравненных превышений (во взаимном положении реперов). Последнее наиболее важно не только для высотных, но и плановых сетей, что уже находит отражение в учебной литературе [7] и должно находить в программных комплексах.

С целью получения равенства диагональных элементов ковариационной матрицы в нивелирной сети в работе [3] ставится требование о необходимости отсутствия исходных пунктов. Вместе с этим равенство диагональных элементов может быть в свободных и несвободных сетях. Покажем это на примерах (рис. 3).

Рис. 3 - Построения с исходными пунктами

На рисунке приведены три построения [1, с. 121]: ход (разомкнутый полигон) с двумя исходными реперами (а); сеть с двумя узловыми точками (система разомкнутых полигонов) и четырьмя исходными реперами (б); свободная сеть (в). Выполним анализ матриц Q для первого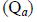 и второго 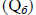построений:

Здесь диагональные элементы каждой матрицы равны, но первое построение приводит к равноточному определению отметок и всех превышений 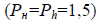. Во втором этого не наблюдается, так как вес превышения между узловыми пунктами равен 2,0, а все остальные превышения и отметки имеют вес 2,7. Таким образом, с позиции равенства погрешностей отметок (диагональные элементы равны) построения равноточны, хотя и присутствуют исходные пункты, а с позиции равенства погрешностей превышений, второе построение не равноточно.

Если рассматривать построения как нуль-свободные (метод "free netwoork adjustment" E. Mitermayer, 1971 [8]), то в этом случае из-за отсутствия невязок задача уравнивания не возникает. Матрица 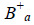приведена в работе В.Н. Ганьшина [1, с. 117], а матрица нами получена, но здесь не приводится. В обеих из них диагональные элементы не равны между собой. Заметим, что метод "free netwoork adjustment" не применим в таких построениях, где его использование приводит к уменьшению или исключению из уравнивания избыточно измеренных величин.

Теперь обратимся к сети (рис. 3, в) [1] и рассмотрим результаты в двух вариантах. В первом, в качестве исходного примем пункт 1, а во втором будем использовать метод "free netwoork adjustment" и данные [1, c. 124]. Запишем матрицы Q и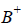

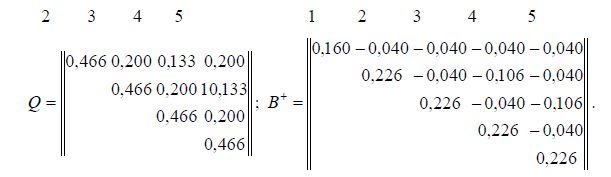
Из приведенных данных следует, что диагональные элементы матрицы Q равны (веса отметок 2,14) и, по мнению авторов [3], сеть будет равноточной, но она свободная (имеет исходный пункт). Коэффициенты корреляции между отметками 0,43 и 0,29, а ее след равен 1,86. Если в качестве исходного последовательно принимать пункты 2, 3, 4 или 5, то в матрице Q диагональные элементы становятся не равными; во всех случаях ее след остается одинаковым и равным 2,20. Коэффициенты корреляции между отметками принимают значения 0,53, 0,60 и 38. Среднее арифметическое из пяти следов матрицы Q будет равно 2,13.

Диагональные элементы второй матрицы 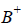не равны (веса отметок 6,25 и 4,4), а поэтому она не равноточна. Однако (рис. 3, в) видно, что она имеет симметричные замыкающие, равноточные превышения уравниваются под условием метода наименьших квадратов с дополнительным условием (нуль-свободная), т.е. выполняются все требования, предъявляемые [3] к топологии сети и методу уравнивания результатов измерений. Вместе с этим, коэффициенты корреляции между отметками поменяли знаки на противоположные и приняли значения -0,18, -0,21, -0,47, а ее след стал равен 1,07. Следовательно, во втором случае за счет изменения начала отсчета произойдет повышение (искажение) точности в 1,4 раза 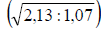, что противоречит классической теории.

Опустив промежуточные вычисления, приведем значения весов уравненных превышений в обоих вариантах по каждому ходу:

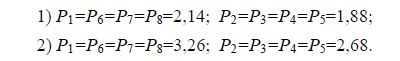
Среднее значение этих весов равно 2,0 и 3,0, в то время как по правилу Ансермета веса измеренных величин при уравнивании повышаются в среднем как отношение n:t (в рассматриваем примере 8:4=2). Значит, во втором случае, когда применяется метод "free netwoork adjustment", правило Ансермета о среднем отношении весов измеренных величин нарушается 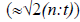. Появление величины 1,41 объясняется введением второго дополнительного условия (7 или 8).

Выводы и предложения.

Таким образом, обработка представленных построений (рис. 1–3) показала, что равенство диагональных элементов обратных матриц может быть в несвободных, свободных и нуль-свободных нивелирных сетях, у которых одинаковое число звеньев (ходов) на каждом определяемом пункте. Уравнивание измеренных превышений в нуль-свободной сети вместо их уравнивания в свободной сети приводит к повышению (искажению) точности уравненных величин в 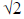раз, что совпадает с выводами [8] для строительных сеток; пропорционально увеличивается и отношение n:t. Однако при такой замене происходит изменение величин и знаков коэффициентов корреляции между определяемыми отметками, но остаются одинаковыми погрешности между уравненными превышениями, т.е. во взаимном положении реперов между которыми измерено(ы) превышение(я), на что ранее уже указывалось [1, 9].

Уравнивание превышений в нуль-свободных нивелирных сетях и ходах без исходных пунктов не согласуется с законом Республики Беларусь "О геодезической и картографической деятельности" от 14 июля 2008 г. №396-З, где в ст.1 даны следующие определения нивелирной сети и специальных геодезических сетей:

нивелирная сеть — система геодезических пунктов на земной поверхности, высоты которых определены относительно исходного пункта, принятого за начало отсчета, или над уровнем моря в общей для них системе высот;
специальные геодезические сети — геодезические сети, создаваемые на локальных участках местности для решения специальных научных и инженерно-технических задач (строительство и эксплуатация сложных инженерных сооружений и др.), требующих определения взаимного положения точек земной поверхности в плане и по высоте со специально заданной точностью, и имеющие связь с государственной геодезической сетью (выделено нами – И.К.).

Из этого следует, что в нивелирной сети специального назначения должен быть исходный пункт и должно определяться взаимное расположение точек (реперов) по высоте. Поэтому, если вводить отсутствующие в законе понятие "равноточная сеть", то следует говорить о равенстве весов уравненных превышений в любой нивелирной сети, а не о равенстве весов отметок определяемых реперов в нуль-свободной сети.

Создать и поддерживать равноточную нивелирную сеть на объекте во время его строительства проблематично, но в этом, видимо, нет и необходимости. На первом этапе следует определить число необходимых реперов [10] и среднюю квадратическую погрешность единицы веса с таким расчетом, чтобы по техническим условиям погрешность определения осадки марки не превышала установленной величины [4, 5] (например, на сжимаемых грунтах 2—5 мм). При этом граф сети должен иметь минимальный периметр [6] и обеспечивать возможность надежной оценки устойчивости реперов в последующих циклах наблюдений. Таким примером на территории Республики Беларусь являлась нивелирная сеть Лукомольской ГРЭС, созданная в 1965 г. Она включала 6 реперов, по 2 рядом (60 м), расположенных по углам равнобедренного треугольника со сторонами 400 и 700 м. К сожалению, в ней в настоящее время осталось 4 репера.

Выявленные смещения являются относительными, так как сравниваются изменения взаимного положения равноценных, с точки устойчивости, реперов. Из-за относительности и неоднозначности разделения величин смещений от их возможных ошибок, задача оценки стабильности реперов и выбора исходного не имеет единственного решения [11].

Однако при оценке устойчивости реперов исходной сети следует отдавать предпочтение методам, основанным на анализе изменений взаимного положения исследуемых реперов при последовательном пересмотре за исходный каждого, входящего в сеть.

Уменьшать число циклов (эпох), как это рекомендовано [3] нельзя. Периодичность и число циклов определяется техническим заданием и проектом производства геодезических работ, который разрабатывается "при строительстве зданий выше девяти этажей, а также других технически сложных и крупных объектов" [5, c.7]. Известно, что время между циклами зависит от завершения отдельных этапов строительства, а не от точности геодезических работ. В каждом цикле исходный репер должен быть определен, а этим исключается оценка точности относительно виртуальной плоскости и точки, имеющим место в нуль-свободной сети. Хотя в ней псевдообратная матрица и обладает наименьшей нормой и следом, а если 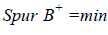, то это соответствует А — оптимальному плану геодезического построения [6, c.11].

В развитие предложений, сделанных авторами [3], в новой работе [12] вводится еще одно понятие "квазиравноточная сеть" (почти равноточная), делается вывод, "что симметричные сети, как правило, жестче несимметричных", а в преамбуле статьи записано: "В практике уравнительных вычислений используется понятие равноточных измерений, соответствующее случаю, когда измерения выполнены с неодинаковой точностью". Приведенные здесь предложения и вычисления, на наш взгляд, требуют более широкого обсуждения.

Список использованной литературы

1. Ганьшин В.Н. Стороженко А.Ф., Ильин А.Г. и др. Измерение вертикальных смещений сооружений и анализ устойчивости реперов. М., «Недра», 1981.
2. Стороженко А.Ф. Еще раз к вопросу об устойчивости глубинных реперов. Сборник научных трудов по геодезии. Под ред. Н.А. Буденкова и А.В. Клименко. Волгоград, 1971, с. 57—61.
3. Усов Д.В., Усова О.О., Ялтыхов В.В. Методика построения равноточных нуль-свободных нивелирных и спутниковых геодезических сетей. «Земля Беларуси», 2009, №1, 38—40.
4. ГОСТ 24846 – 81 Грунты. Методы измерения деформаций оснований зданий и сооружений. М., Изд-во стандартов, 1981.
5. Технический кодекс установившейся практики. Геодезические работы в строительстве. Правила проведения: ТКП 45-1.03-26-2006 (02250) — Введ.1.07.06 взамен СНиП 3.01.03-84.Мн., Мин.-во строительства и архитектуры, 2006.
6. Тамутис З.П. Оптимальные методы проектирования геодезических сетей. М., «Недра», 1979.
7. Harvey B.R. Practical Least Squares and Statistics for Survey. Monograph 13, School of Geomatic Engineering. The University of New South Wales, 2nd Ed., 1994.
8. Василевски А., Сикорски К. Исследование точности уравненных координат пунктов строительных сеток с применением обобщенной обратной матрицы. Республиканский межведомственный научно- технический сборник. Инженерная геодезия, выпуск 23. Под ред. В.Е. Михайленко. Киев, «Будiвельник», 1980, с. 47—49.
9. Барсук А.В., Картавенков И.Г. О свойстве псевдообратной матрицы в свободных сетях. Новополоцкий политех. ин-т., Новополоцк, 1988. Деп. в ОНИПР ЦНИИГАиК 11.07.88. №328-ГД.
10. Цюнько В.И. Графоаналитический способ определения необходимого количества реперов для наблюдений за осадками сооружений. Сборник научных трудов по геодезии. Под ред. Н.А. Буденкова и А.В. Клименко. Волгоград, 1971, с. 68—70.
11. Михелев Д.Ш., Рунов И.В., Голубцов А.И. Геодезические измерения при изучении деформаций крупных инженерных сооружений. М., «Недра», 1977.
12. Мицкевич В.И., Куприенко Н.О., Усов Д.В. О квазиравноточных нивелирных сетях, получаемых при уравнивании равноточных построений методом Lp-оценок. Вестник Полоцкого госуд. ун-та. Серия F «Строительство». Прикладные науки, 2009, №12, с. 132—135.