ТЕНДЕНЦІЇ ВИКОРИСТАННЯ БАГАТОВИМІРНОГО РОЗПОДІЛУ ПРИ АНАЛІЗІ РЕЗУЛЬТАТІВ ГЕОДЕЗИЧНИХ ВИМІРЮВАНЬ
Автор: Войтенко С.П., Білоус М.В.
Розглянуто шляхи використання числових характеристик багатовимірного розподілу для виявлення стану стабільності пунктів геодезичних мереж, дослідження деформацій інженерних споруд та ін.
Постановка проблеми.
При дослідженні різноманітних виробничих процесів геодезичними методами постає ряд практичних завдань з виявлення їх стану, стабільності, характеру можливих деформацій для прийняття конкретних рішень щодо їх подальшого використання, або для розробки інженерних рішень щодо їх стабілізації. Для цього пропонується використати числові характеристики багатовимірного розподілу результатів геодезичних вимірювань.
Огляд попередніх публікацій.
Питання дослідження багатовимірного розподілу і встановлення функцій розподілу та його числових характеристик висвітлено в роботах з теорії ймовірності та математичній статистиці [1-3]. Проблема полягає в тому, щоб використати властивості багатовимірного розподілу при аналізі результатів геодезичних вимірів.
Постановка завдання.
Завданням наукового дослідження є визначення оптимальних характеристик параметрів багатовимірного розподілу результатів вимірів, і на основі їх аналізу виявити внутрішні процеси, що відбуваються під час спостережень на об’єкті.
Основний зміст роботи.
В геодезичних мережах при дослідженнях деформацій інженерних споруд може одночасно вимірюватись n-величини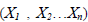 
. За результатами багаторазових вимірів отримують n-вимірну матрицю вектор X:
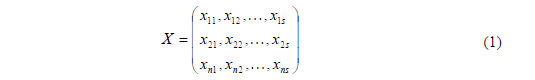
Його можна характеризувати інтегральною функцією розподілу 
та диференційною функцією розподілу
Однак для багатовимірного розподілу функцій розподіл (2) має досить складний вигляд [2]. Тому для системи n-випадкових величин за результатами вимірювань 
можна визначити числові характеристики параметрів n-вимірного розподілу. При практично незмінному комплексі умов, коли результати вимірів підкорюються нормальному закону розподілу можна обчислити емпіричні (статистичні) математичні сподівання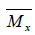 
, або середні арифметичні із кожного ряду вимірів
де 
Вони характеризують найбільш імовірне значення кожної випадкової величини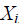 
.
Другою важливою характеристикою n-вимірного розподілу є узагальнене поняття дисперсії або міри точності n-вимірного вектора Х.
Згідно [1] для n-отриманих результатів системи 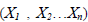узагальненим значенням дисперсії є кореляційна матриця 
:
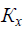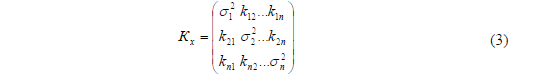
Аналіз формули (3) показує, що по діагоналі розміщені дисперсії випадкових величин 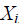, які і характеризують міру їх точності.
За результатами вимірів можна обчислити емпіричні значення дисперсій
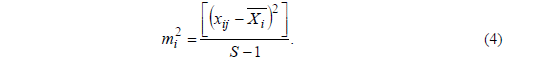
Кореляційна матриця 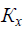містить кореляційні моменти 
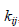, які симетричні відносно головної діагоналі, яку утворюють дисперсії 
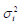, їх обчислюють за формулою
де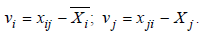 
Відомо, що елементи 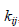кореляційної матриці 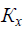характеризують міру залежності або зв’язку між випадковими величинами 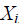та 
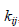. Тому по величині можна оцінити як в експерименті взаємодіють досліджувані величини. В якості досліджуваних величин можуть бути пункти геодезичних мереж, кути, перевищення, деформаційні марки і т.п. Тому аналіз величин отриманих кореляційних моментів дозволяє визначити якісні характеристики поведінки випадкових величин в просторі або часі.
Однак кореляційні моменти мають розмірність і тому в практичному використанні не досить зручні, оскільки не дозволяють виконувати порівняльний аналіз із аналогічними дослідженнями виконаними в іншій період часу або на іншому об’єкті.
Для зручності розраховують нормовану кореляційну матрицю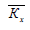 
[1].
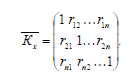
Коефіцієнти кореляції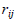 
обчислюють за формулою
Середні квадратичні похибки 
обчислюють за формулою (4). Відомо, що коефіцієнти кореляції 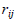є безрозмірними і можуть приймати значення 
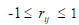. Тому вони дозволяють більш об’єктивно виконувати порівняльний аналіз складових n-вимірного вектора X як в окремому експерименті, так і в часі та просторі. Вважається, що коли 
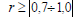, то залежність сильна або має прямолінійний характер. При 
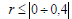– вона вважається незначною.
Достовірність коефіцієнта кореляції обчислюється за формулою
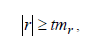
де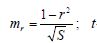 
- параметр, який вибирається із таблиць розподілу Лапласа або Стюдента залежно від кількості вимірів.
Так, при дослідженнях осідань інженерних споруд поблизу їх створюють кущ, як правило, із трьох глибинних реперів, які за умовами повинні зберігати високий рівень стабільності у вертикальному відношенні. Для цього виконують визначення перевищень між ними в кожному циклі спостережень.
Відомо декілька способів математичного обґрунтування їх стабільності. Однак застосування вищенаведеного математичного апарату дозволить більш достовірно встановити найбільш стабільний репер на основі аналізу емпіричних математичних сподівань, дисперсій виміряних перевищень та міри залежності між ними (коефіцієнтів кореляції 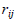) за наведеними формулами. При цьому в матриці - векторі X (1) за приймають виміряні перевищення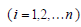 
в циклах спостережень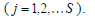 
Теорію багатовимірного розподілу доцільно застосовувати при дослідженнях деформацій інженерних споруд. Тоді в матриці (1) за величину n беруть позначки осідальних марок або реперів, які визначаються в S циклах спостережень. Це дає змогу визначити як їх стабільність, так і залежність між ними. А це в свою чергу буде характеризувати і взаємодію конструктивних елементів, дозволить конструкторам більш якісно розробляти проекти з усунення деформацій споруди в цілому і її окремих вузлів та елементів.
Можливі інші сфери використання властивостей характеристик багатовимірного розподілу.
Розглянемо більш глибокий приклад використання запропонованого математичного апарату. Відомо, що характер поведінки деформаційних знаків у часі та між собою можна описати певним видом функціональної залежності. Разом з тим можна математично описати функціональну залежність стабільності по кожному деформаційному знаку.
Для кожного випадку отримаємо систему функцій, що дасть можливість визначити математичні сподівання та кореляційну залежність між функціями. Їх комплексний аналіз приведе до більш глибокого вивчення причин деформаційних процесів та розробки проектів щодо їх стабілізації.
Висновки.
Література
1. Войтенко С.П. Математична обробка геодезичних вимірів. Теорія похибок вимірів / С.П. Войтенко. – К.: вид-во. Бучасової С.Г., 2003. – 215 с.
2. Войтенко С.П. Теория математической обработки геодезических измерений / С.П. Войтенко, В.С. Заречный. – Краснодар: ООО "Издательский дом - ЮГ". – 2007. – 238 с.
3. Большаков В.Д., Маркузе Ю.И. Практикум по теории математической обработки геодезических измерений / В.Д. Большаков, Ю.И. Маркузе. – М.: Недра, 1984.-352 с.