Кудряшов А.П - Извлечение и сопоставление точечных особенностей

В статье представлен метод извлечения точечных особенностей изображения, которые используются для нахождения соответствия между различными видами объекта или сцены. Найденные особенности инвариантны к изменению освещения сцены, и достаточно устойчивы к изменению точки наблюдения. Предлагаемый подход позволяет достаточно хорошо определять и отслеживать точечные особенности на серии изображений одной сцены, снятой с разных точек наблюдения. По найденным соответствиям строится фундаментальная матрица, необходимая в задачах реконструкции трехмерных сцен. Время расчета определяется количеством найденных особенностей и практически не зависит от размера изображения.

Введение

Нахождение соответствий на изображениях – одна из основных проблем в машинном зрении. Без этого невозможно сопоставление объектов и восстановление трехмерной структуры. Также задача отслеживания особенностей актуальна при отслеживании движения [9], определении местоположения мобильного робота, калибровки камеры [8] и других приложений [1].

В последнее время указанной проблеме было уделено достаточно много внимания и, как следствие, достигнут существенный прогресс в этом направлении, однако в целом задача сохраняет свою актуальность из-за растущих потребностей приложений. С обзором по этой теме можно познакомиться, например, в работах [4, 6]. Наиболее известным и широко применяемым методом является детектор Харриса [2], который позволяет находить большое количество точечных особенностей с высокой скоростью. Сопоставление особенностей происходит путем сравнения их окрестностей кросскорреляционным [5] или другим методом. Но на больших по размеру изображениях сразу несколько особенностей на первом изображении могут оказаться близкими к одной и той же особенности на втором изображении. И отличить ложные соответствия от верных не всегда возможно. Более эффективным является алгоритм Scale Invariant Feature Transform (SIFT) [6]. Он лишен части недостатков вышеописанного алгоритма, но обладает высокой сложностью обработки. Хотя авторы пишут, что алгоритм SIFT работает в реальном масштабе времени, эксперименты с рабочей версией программы. показали, что данная скорость достигается лишь при размере входного изображения примерно 320*240 точек. При размере изображения в 3 мегапикселя обработка пары снимков требует уже 2-3 минут. Но для решения задач некоторых задач, например, реконструкции трехмерных сцен городской обстановки по фотоизображениям необходимо более высокое разрешение, порядка 5-10 мегапикселей. Поэтому в данной работе была поставлена задача разработки алгоритма с более высокой скоростью выделения точечных особенностей и с приемлемыми для указанного приложения достоверностью и количеством особенностей. Результатом выполненной работы стал описываемый ниже алгоритм, который обеспечивает достаточно устойчивое нахождение точечных особенностей на больших по размеру изображениях со сравнительно высокой скоростью обработки.

Описание алгоритма

Схематично работа алгоритма может быть представлена следующим образом:

Уменьшение разрешения изображения до оптимального. Для рассматриваемого приложения оптимальное разрешение было установлено экспериментальным путем и составило примерно 400*300 точек. Указанное разрешение при необходимости может изменяться.
На уменьшенном изображении ищутся точечные особенности с помощью метода, получившего название Difference-of-Gaussian (DoG) [6].
По полученным на предыдущей стадии точечным особенностям на паре уменьшенных изображений ищутся соответствия. Поиск происходит с помощью двух методов: кросскорреляционного [5] и метода нормированного евклидового расстояния.
Перерасчет полученных соответствий с уменьшенных изображений на исходные. При этом, поскольку каждому пикселю на малом изображении соответствует участок пикселей на большом, учитывается возможное неточное сопоставление.
Применение фильтра, позволяющего избавиться от большинства ложных сопоставлений.
Расчет фундаментальной матрицы [3,7] с помощью выбора наиболее правдоподобных особенностей или методом RANSAC [9].

Главная особенность данного метода заключается в том, что, поскольку, большая часть вычислений проводится на уменьшенных изображениях, вычислительная сложность алгоритма уменьшается на порядок, по сравнению с тем, если бы вычисления производились на исходных изображениях.

Нахождение точечных особенностей

В большинстве работ, посвященным выделению и отслеживанию точечных особенностей [2,4,5,9], рекомендуемый размер изображения в большинстве случаев лежит в диапазоне от 320*240 до 800*600 пикселей, и это не случайно. Поскольку большие исходные изображения больше подвержены цифровому шуму матрицы, то верные сопоставления имеют меньший коэффициент сходства, а при снижении проходного порога этого коэффициента в обработку попадает большое количество ложных сопоставлений. Также на больших изображениях приходится рассматривать физически более мелкие участки сцены, и при их сопоставлении также возникает большое количество ложных участков.

Поэтому в данном методе первым шагом разрешение изображений уменьшается с исходного до 400*300 пикселей. Это позволяет, во-первых, уменьшить влияние шума на изображении, а во-вторых, позволяет рассматривать физически более крупные участки сцены. Например, на 1-мегапиксельном снимке участок 10*10 пикселей вокруг найденной особой точки соответствует размеру 30*30 сантиметров, а такой же участок на снимке размера 400*300 соответствует 260*260 сантиметров. Поэтому, наряду с увеличением скорости обработки уменьшенные снимки позволяют избавиться от большинства неоднозначностей сопоставления особенностей, как показано на рисунке 1.

Рисунок 1 – Неоднозначность на исходном изображении (1.а) и определенность на уменьшенном (1.б) при одинаковом размере окрестности

Как было указано выше, нахождение точечных особенностей выполняется с помощью функции Difference-of-Gaussian. Для каждой точки изображения определяется функция сглаживания:

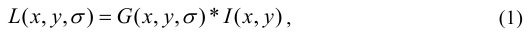
где I(x, y) - цвет точки с координатами (x, y), а 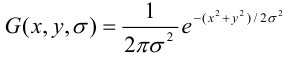– функция Гаусса.

Для нахождения особых точек необходимо получить функцию D(x, y) , которая вычисляется как разница двух различных функций размытия с различными значениями σ :

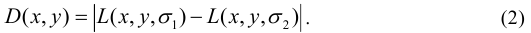
Далее необходимо вычислить локальные максимумы, которые и будут являться особыми точками. Для каждой точки рассмотрим окрестность заданного радиуса. Если в этой окрестности есть точка, значение D(x, y) которой больше чем у рассматриваемой точки, то рассматриваемую точку удаляем из дальнейшего рассмотрения, иначе оставляем и переходим к следующей точке. Следует заметить, что для двух сравниваемых изображений особые точки необходимо находить по-разному. На втором изображении необходимо получить более плотное облако особенностей, чем на первом. Это связано с тем, что изменение точки наблюдения ведет к изменению освещенности, что может повлиять на нахождение особых точек при тех же параметрах, что и на первом изображении. Этот эффект можно уменьшить уменьшением окрестности поиска локального экстремума, что приведет к более плотному облаку особенностей на втором снимке.

Сопоставление точечных особенностей

После нахождения особых точек на паре изображений необходимо их сопоставить. В ходе экспериментов было выяснено, что кросскорреляционный метод и метод евклидовых расстояний дают приемлемые, но часто различные результаты, поэтому было принято решение использовать их совместно, для нахождения большего числа сопоставлений. Далее кратко рассмотрим эти методы.

Кросскорреляционный метод заключается в том, что окрестность каждой найденной особенности на первом изображении сравнивается с окрестностью каждой особенности на втором изображении по следующей формуле:

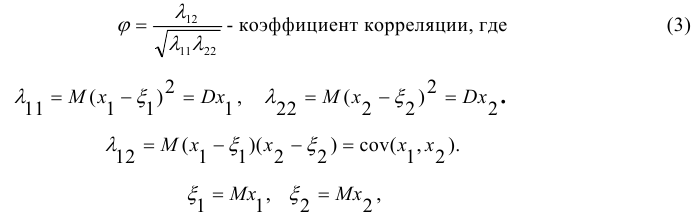
x₁ - изображение участка с первого снимка,

x₂ - изображение участка со второго снимка.

M(x)- математическое ожидание

D(x)- дисперсия

Для ускорения алгоритма можно сравнивать не все особенности второго изображения, а только лежащие в определенной окрестности особенности первого изображения.

Метод евклидовых расстояний также заключается в сравнении окрестностей особенностей с двух снимков, но коэффициент сходства ищется по другой формуле:

где C_i,j – нормированный цвет точки окрестности особой точки с первого и второго изображения.

В общем случае метод евклидовых расстояний сильно зависит от изменения освещенности, поэтому вместо цвета пикселя берется нормированный цвет по окрестности вокруг рассматриваемой особой точки:

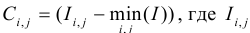- цвет точки окрестности.

Теоретически коэффициент сходства между правильно сопоставленными особенностями должен быть равен единице. Но в действительности коэффициент корреляции будет меньше. В проводимых экспериментах его значение обычно составляло 0.75. Повышение порога (увеличение коэффициента) позволяет понизить количество ложных сопоставлений, однако при этом уменьшается и количество сопоставленных пар. Поэтому был разработан метод рекуррентной достройки соответствий по следу ближайшей сопоставленной пары особенностей. Для каждой несопоставленной особенности первого изображения ищется ближайшая сопоставленная особенность. Поскольку мы знаем в ней направления перехода особенности первого изображения в особенность второго, то можно для несопоставленной особенности также указать направление и провести поиск в небольшой окрестности найденной точки, и получить еще одно сопоставление. Данный метод иллюстрируется на рис. 2.

Рисунок 2 – Зеленым цветом показана сопоставленная пара особенностей; на основе ее направления, для несопоставленной особенности из первого изображения строится небольшая окрестность на втором изображении, в которой ищется сопоставление.

Перерасчет сопоставленных пар на исходных изображениях

Каждому пикселю на уменьшенном изображении соответствует участок пикселей на большом исходном изображении. Размер этого участка составляет nxn, где 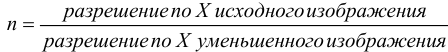. На этом участке необходимо найти особую точку. Для этого рассчитаем средний цвет пикселей на этом участке по формуле: 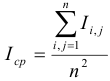Затем найдем наиболее отличающуюся точку по формуле: 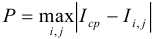- это и будет искомая особая точка на первом изображении. Для поиска соответствующей ей точки на втором изображении необходимо сравнить кросскорреляционным методом все точки на участке размерности mЧm,г де m = 2 . Увелиnчение размера участка сделано для того, чтобы учесть возможное отклонение соответствующих точек на уменьшенном изображении на 1 пиксель. Как было отмечено выше, коэффициент корреляции одной и той же пары точек на исходном изображении будет меньше, чем на уменьшенном, поэтому пороговое значение коэффициента корреляции уменьшаем на 0.1.

Фильтрация полученных соответствий

Среди найденных соответствий могут быть ложные, так называемые выбросы. Если построить векторное поле соответствующих пар, где началом вектора является координаты точки на первом изображении, а концом - координаты на втором, то правильные соответствия будут иметь определенную закономерность, а выбросы этой закономерности подчиняться не будут. Это показано на рис. 3.

Рисунок 3 – Векторное поле соответствий.

Выбросы можно удалить рекуррентным фильтром. Для каждой группы векторов, лежащих в заданной окрестности, рассчитывается средняя длина вектора и угол наклона. Все вектора, чьи длина и угол отличаются более чем на заданную величину отклонения от среднего - удаляются, и вся процедура повторяется с более жесткими значениями максимально допустимого отклонения от среднего. Эта процедура работает при количестве трех и более векторов в группе. Если же в группе всего один вектор, то ищется ближайший и добавляется в эту группу. Если в группе два вектора, то рассчитывается угол и длина отличия одного от другого, и если они не превосходят порогового значения, то вектора считаются верными. Иначе к этой группе добавляется ближайший вектор, и расчет проводится как для групп, где три и более векторов. Результат работы фильтра продемонстрирован на рис. 4.

Рисунок 4 – Векторное поле соответствий после применения фильтра.

После нахождения соответствий может быть построена фундаментальная матрица [3]. Она строится с помощью 8-ми точечного алгоритма [7], либо по восьми точкам с наибольшим коэффициентом сходства, либо с помощью алгоритма RANSAC.

Обсуждение результатов

В вычислительных экспериментах использовались серии фотоизображений реальной городской обстановки с различными величинами разрешения. Для оценки эффективности предложенного алгоритма было выполнено сравнение характеристик его работы с упомянутым во введении алгоритмом SIFT. Результаты сравнения приведены в таблице 1.

Таблица 1

№	Размер изображения	Кол-во найденных пар	Ложных	Время (сек)	Кол-во найденных пар(SIFT)	Ложных	Время (сек)
1	1632*1224	51	3	7	104	2	47
2	2048*1536	92	2	5	217	2	116
3	800*600	18	0	3	13	0	7

Из таблицы видно, что предлагаемый алгоритм в сравнении с алгоритмом SIFT за счет меньшего количества сопоставлений (но вполне приемлемого для целей рассматриваемого приложения) обеспечивает существенно более высокую скорость работы при практически такой же достоверности результатов.

Заключение

В статье представлен метод выделения/сопоставления точечных особенностей по паре изображений и нахождение по ним фундаментальной матрицы. Проведенные вычислительные эксперименты позволяют говорить об эффективности и достаточной устойчивости работы алгоритма. В дальнейшем планируется: оптимизация работы программы для ускорения обработки данных и увеличения числа идентифицируемых особенностей и применение алгоритма в задаче реконструкции трехмерной сцены городской обстановки по некалиброванным фотоизображениям.

Список использованной литературы

1. В.А. Бобков, Ю.И. Роншин, А.П. Кудряшов. Сопоставление линий по трем видам пространственной сцены// Информационные технологии и вычислительные системы,№2, 2006, С. 71-78.
2. Harris, C. and Stephens, M. 1988. A combined corner and edge detector. In Fourth Alvey Vision Conference, Manchester, UK, pp. 147-151.
3. Luong, Q.T., and Faugeras, O.D. 1996. The fundamental matrix: Theory, algorithms, and stability analysis. International Journal of Computer Vision, 17(1):43-76.
4. Mikolajczyk, K. 2002. Detection of local features invariant to affine transformations, Ph.D. thesis, Institut National Polytechnique de Grenoble, France.
5. Basri, R., and Jacobs, D.W. 1997. Recognition using region correspondences. International Journal of Computer Vision, 25(2):145-166.
6. David G. Lowe Distinctive Image Features from Scale-Invariant Keypoints International Journal of Computer Vision, 60, 2 (2004), pp. 91-110
7. Hartly R. In defence of 8-point algorithm, Proceedings of the International Conference on Computer Vision 1995, pp 1064 – 1070.
8. Manolis I.A. Lourakis and Rachid Deriche. Camera self-calibration using the singular value decomposition of the fundamental matrix. In Proc. of the 4th Asian Conference on Computer Vision, volume I, pages 403–408, January 2000.
9. D.Nister, “Preemptive RANSAC for live structure and motion estimation” ICCV Proc, pp.199- 206, 2003.