Инвариантные алгоритмы сопоставления точечных особенностей на изображениях
Автор: Виктор Гаганов
Источник: http://cgm.computergraphics.ru/issues/issue17/invariant_features
Автор: Виктор Гаганов
Источник: http://cgm.computergraphics.ru/issues/issue17/invariant_features
Обнаружения и сопоставление точечных особенностей на изображениях является важной задачей компьютерного зрения и находит применение в таких приложениях как 3D реконструкция, индексация в базах данных изображений и т.д. На первый взгляд наборы соответствующих точек на изображениях дают довольно мало информации об изображениях и наблюдаемой сцене, но на самом деле это не так. Например, если у нас есть несколько изображений одной сцены и наборы соответствующих точек на этих изображениях мы можем определить настройки и положение камеры для каждого изображения. К сожалению, на данный момент нет универсального алгоритма качественно решающего данную задачу. Связано это с тем, что при съемке сцены изображения ее точек подвергаются различным искажениям, например проективные преобразования, связанные с перемещением камеры либо объектов сцены, изменения освещенности сцены и т.д. В данной статье будут рассказано о некоторых принципах построения алгоритмов сопоставления точечных особенностей, инвариантных к таким искажениям как изменение масштаба, вызванное например оптическим или цифровым zoom'ом, поворот изображения и изменения освещенности сцены.
Рассмотрим задачу более детально. Пусть нам даны 2 изображения некоторой сцены. Требуется найти набор пар точек (x1,i,y1,i) (x2,i,y2,i) i=1..N таких, что (x1,i,y1,i) (x2,i,y2,i) являются изображениями одной и той же точки в 3D. Заметим, что для сопоставления подходят далеко не все точки изображения (рис 1). Например, очень сложно найти соответствующую точку для некоторой точки изображения однородной поверхности. Поэтому для сопоставления используются т.н. особые точки. Особая точка изображения m - это такая точка изображения, окрестность которой o(m) можно отличить от окрестности любой другой точки изображения o(n) в некоторой другой окрестности особой точки o2(m). Более детальное описание особых точек изображения приводится, например в [2].

Рисунок 1 – Слева точка, которая является особой, справа точка, которая не является особой
Важным свойством любого алгоритма сопоставления особенностей является набор искажений изображения особой точки, с которыми он способен справиться. Обычно выделяют следующие виды искажений:
Для начала рассмотрим простейший, уже ставший классическим, алгоритм сопоставления особенностей на изображениях и его свойства. Алгоритм работает по следующей схеме:
Приведенный выше алгоритм подходит разве что для сопоставления особенностей в кадрах видеопоследовательности т.к. он крайне неустойчив к любым видам искажения изображения особых точек. Например, при повороте камеры изображения окрестностей особых точек изменяются настолько сильно что алгоритм практически не дает верных соответствий. Аналогичная ситуация наблюдается и с изменением масштаба изображения. Единственный вид искажений, которым данный алгоритм способен противостоять - изменения освещенности (для этого надо проводить нормировку окрестностей особенностей).
Другая проблема алгоритма связана с повторяемостью обнаружения особенностей детектора Харриса и ему подобных детекторов. Например, при условии существенного изменения масштаба для пары изображений наборы особых точек которые выдает детектор Харриса имеют крайне мало пересечений т.е. то что являлось особой точкой на первом изображении в большинстве случаев не является особой точкой на втором изображении.
Указанные причины делают практически невозможным применение данного алгоритма на практике при наличии таких искажений как изменение масштаба и поворот. О том, как эти трудности преодолеть, и пойдет речь далее.
Для того чтобы решить проблему изменения масштаба применяются т.н. scale-space детекторы особенностей. Такие детекторы помимо пространственного положения особенности (x,y) оценивают также локальный масштаб особенностей s, который отражает "размер" особенности на изображении. Существует множество таких детекторов особенностей, описания некоторых из них можно найти в [1,3,4,6]. В статье мы опишем упрошенный детектор Харриса-Лапласа т.к. это один из лучших scale-space детекторов особенностей, и при этом он может быть крайне эффективно реализован.
Введем понятие scale-space представления изображения. Определение: Пусть I = I(x,y) - функция двух аргументов, тогда scale-space представлением функции I = I(x,y) называется функция трех аргументов L(x,y,σ) = (g(•,σ)*I(•)(x,y), где g(x,y,σ) = ex2+y2/2σ2/2σ2π, * - символ, обозначающий свертку, а L(•,0) = I(•)
Таким образом scale-space представление изображения есть размытие изображения при помощи свертки Гауссианом g с разными значениями параметра размытия σ. Заметим что понятие scale-space определено для полутонового изображения и если вы работаете с цветным изображением в формате RGB следует сначала привести его к полутоновому.
При работе со scale-space представлением изображения используются т.н. нормированные производные, которые определяются следующим образом. La,norm(•,σ) = σ(∂aL)(•,σ) = σ(∂a(g*I))(•,σ) - производная от L по а (a - направление взятия производной, вместо а можно подставить x или y). Заметим что основное отличие нормированных производных от обычных - то что производная умножается на значение масштаба σ. При использовании производных порядка большего чем 1 следует возвести σ в степень равную порядку производной, например Lxx,norm(•,σ) = σ2(∂xxL)(•,σ) и т.д.
Это крайне неполное описание понятия scale-space представления изображения, но для дальнейшего изложения нам этого вполне достаточно. Более подробное описания, которое включает в себя scale-space представление многомерное функции, более общий вид нормированных производных, их свойства и т.д. можно найти в [3,5].
Теперь полностью опишем алгоритм работы упрошенного детектора Харриса-Лапласа.
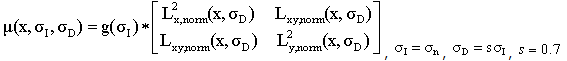
Заметим, что именно использование многих уровней масштаба решает проблему повторяемости обнаружения особенностей. Если при сильном изменении масштаба обычный детектор Харриса не мог обнаружить большую часть особенностей из первого изображения на втором изображении, то упрошенный детектор Харриса-Лапласа обнаружит их, просто они будут обнаружены на другом уровне масштаба. Пример работы алгоритма можно увидеть на рисунке 2. Зелеными точками на изображении отмечены положения особенностей на изображении, а синие окружности отражают масштаб особенности, причем r = 3∂, где r - радиус окружности, а ∂ - масштаб особенности.

Рисунок 2 – Пример работы упрощенного детектора Харриса-Лапласа
Для сопоставления обнаруженных особенностей используются т.н. дескрипторы особенностей. Дескриптор особенности - вектор числовых характеристик окрестности особенности D(x) = [f1(w(x))...fn(w(x))] . При сопоставлении особенностей, для принятия решений о том, соответствуют ли друг другу особенности или нет, сравниваются именно дескрипторы этих особенностей. Простейший пример дескриптора особенности - сама окрестность особенности, записанная в виде вектора. Далее будет рассказано, как добиться того, чтобы дескрипторы особенностей были инвариантны к некоторым видам искажений изображения окрестности особенности.
При использовании scale-space детектора особенностей добиться инвариантности к изменению масштаба очень просто. Для этого достаточно перед вычислением дескриптора провести нормировку в соответствии с локальным масштабом особенности, например если с особенностью ассоциирован масштаб 2, то окрестность особенности следует масштабировать с коэффициентом ½ и т.д. Если дескриптор состоит из выражений, в которых используются исключительно нормированные производные, то масштабировать окрестность не обязательно. Достаточно рассчитывать значения производных для значения масштаба σ, который ассоциирован с особенностью.
Самый простой метод добиться инвариантности к повороту при сопоставлении особенностей - использовать дескрипторы, компоненты которых инварианты к повороту. Все производные в выражении - нормированные производные. Далее приводится пример дескриптора из [1], каждая компонента которого инвариантна к повороту:
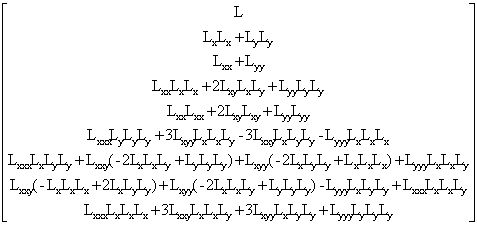 .
.Серьезным недостатком этого метода является то, что в дескрипторе нельзя использовать компоненты, которые не инвариантны к повороту, а число операторов, которые инвариантны к повороту, и при этом применимы на практике, ограничено. Еще одни способ добиться инвариантности к повороту - предварительно нормировать окрестность точки особым образом, чтобы скомпенсировать поворот, и лишь потом вычислять дескрипторы для особенности. Для того чтобы нормировать окрестность по повороту требуется оценить т.н. ориентацию особенности (см. рис 3). Существует много методов оценки локальной ориентации особенности, все они так или иначе используют направление векторов градиентов в окрестности особенности. Мы опишем метод Lowe, предложенный им в [4].
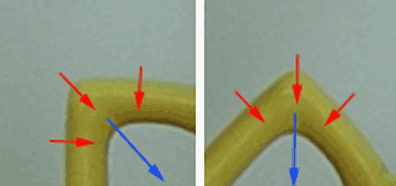
Рисунок 3 – Окрестность особой точки. Красным указаны направления градиентов, а синим показана ориентация особенности
После того, как была вычислена ориентация особенности, произвести нормировку очень просто - для этого достаточно повернуть особенность на угол (−φ) вокруг центра особенности. К сожалению, для некоторой части особенностей ориентация оценивается неверно (обычно 10-20%) и дескрипторы этих особенностей оказываются абсолютно непригодны к сопоставлению. Именно это является основным недостатком данного подхода.
Для того чтобы сделать дескриптор инвариантным к изменению освещенности нужно для начала ввести модель этого изменения. Обычно применяют т.н. аффинную модель, которая подразумевает, что значения пикселей окрестности при изменении освещенности меняется по следующему закону: Î = a·I(x) + b. Это модель не очень точно соответствует действительности и реально процессы, происходящие в пикселях при изменении освещенности намного сложнее, но в силу того, что особенности локальны и имеют небольшой размер такой модели более чем достаточно. Учитывая принятую модель можно использовать следующий алгоритм, устраняющий влияние освещенности на значение пикселей в окрестности особенности: Imean(w(x)) = I(w(x)) - mean(I(w(x))), Iresult(w(x)) = Imean(w(x))/std(I(w(x))), mean(I(w(x))) и std(I(w(x))) обозначают выборочное среднее и среднее квадратичное отклонения в окрестности w, Imean(w(x)) - окрестность, скомпенсированная по переносу, а Iresult - результирующая окрестность, скомпенсированная по освещенности. Именно по особенности Iresult следует вычислять дескриптор особенности, чтобы добиться инвариантности к изменениям освещенности. Также можно составлять дескриптор из функций, которые инвариантны к аффинным изменениям освещенности, далее приводится инвариантный к повороту дескриптор из [1], преобразованный таким образом, чтобы его компоненты были инвариантны к изменениям освещенности. Стоит заметить, что для того чтобы сделать дескриптор инвариантным к изменениям освещенности пришлось удалить первые две его компоненты. Все производные в выражении - нормированные производные:
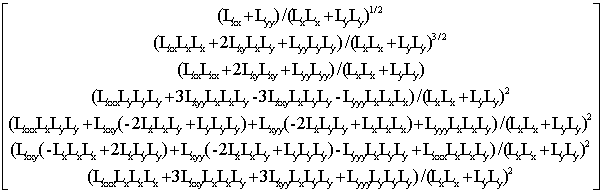 .
.После того как для каждой особенности на паре изображений рассчитаны дескрипторы можно непосредственно приступить к сопоставлению особенностей. Существует множество вариантов алгоритмов сопоставления особенностей по их дескрипторам, их описания можно найти, например в [1] и [6]. Мы предлагаем следующую схему, которая совмещает алгоритмы из [1] и [6].
Обозначим наборы особых точек первого и второго изображения A={ai,i=1..n}, B={bi,i=1..m} , а их дескрипторы DA={DA,i,i=1..n}, DB={DB,i,i=1..m}. Будем считать что дескрипторы - вектора столбцы.
Далее приводятся примеры результатов сопоставления особенностей для нескольких различных пар кадров. Для обнаружения особенностей использовался упрошенный детектор Харриса-Лапласа. В качестве дескрипторов при сопоставлении выступала сама окрестность особенности размером 11x11 пикселей с предварительной нормированная по масштабу, освещенности и повороту. На рисунке 4 изображена пара изображений, которые связаны между собой поворотом вокруг оптической оси камеры и изменением масштаба. Для этой пары изображений были сначала найдены 100 лучших соответствий, по этим соответствиям была оценена гомография, после чего были заново посчитаны 100 лучших соответствия с учетом гомографии.

Рисунок 4 – Пара изображений с посчитанными точечными соответствиями. Красными точками отмечены особенности. Зеленые отрезки - т.н. "следы" особенностей
На рисунке 5 можно увидеть более сложную пару изображений. При съемке второго изображения камера была перенесена на несколько метров вперед. При движении камеры вперед окрестности точечных особенностей подвергаются проективным искажениям что осложняет задачу поиска соответствий. Для этой пары изображений были посчитаны 100 лучших соответствий, потом по ним была рассчитана фундаментальная матрица, после чего были посчитаны 100 лучших соответствий с учетом фундаментальной матрицы (выведены только 20 из них для того чтобы было проще воспринимать картинку).

Рисунок 5 – Пара изображений с рассчитанными соответствиями и эпиполярной геометрией. Красным цветом изображены эпиполярные линии. Пронумерованные зеленые точки - соответствия.
На рисунке 6 изображена пара изображений, которые связаны между собой сильным поворотом камеры. Для этой пары изображений были сначала найдены 100 лучших соответствий, по этим соответствиям была оценена гомография, после чего были заново посчитаны 100 лучших соответствия с учетом гомографии (выведены только 20 из них для того чтобы было проще воспринимать картинку).
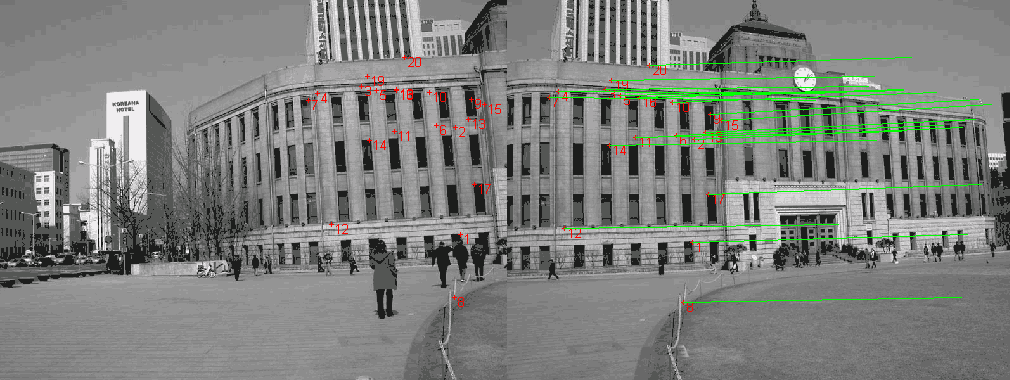
Рисунок 6 – Пара изображений с посчитанными точечными соответствиями. Красными точками отмечены особенности (они пронумерованы). Зеленые отрезки - "следы" особенностей.
1. Krystian Mikolajczyk, "Detection of local features invariant to affine transformations", 2002
2. Антон Конушин, "Слежение за точечными особенностями сцены (Point feature tracking)", 2003
3. Tony Lindeberg, "Feature Detection with Automatic Scale Selection", 1998
4. David G. Lowe "Object Recognition from Local Scale-Invariant Features", 1999
5. Tony Lindeberg, "Scale-space theory: A basic tool for analysing structures at different scales", 1994
6. Adam Baumberg, "Reliable Feature Matching Across Widely Separated Views", 2000
7. Chris Harris, Mike Stephens, "A combined corner and edge detector", 1988