Александр Кравцов, Владимир Вежневец - Общая формулировка задачи внешней калибровки камеры

Одной из центральных задач в области машинного зрения (Computer Vision) является задача определения ориентации и расположения камеры в пространстве по изображению, полученному с ее помощью. Эту задачу также называют задачей внешней калибровки камеры или определения ее внешних параметров.Решение данной задачи требуется в различных областях: картографии, системах распознавания объектов, в расширенной реальности, системах управления компьютером посредством определения положения рук или направления взгляда, системах управления роботами и т.д. Во многих случаях геометрия некоторых объектов сцены известна заранее. На основании этого рассматривается модель, представляющая собой набор черт и их взаимное расположение. Модель налагает ограничения и сужает область решений задачи. В качестве черт используются определенные точки (вершины), отрезки (грани) и углы объекта. В зависимости от используемых черт выделяются следующие постановки задачи внешней калибровки: PnP проблема (Perspective n Points problem), PnL проблема (Perspective n Lines problem) и PnA проблема (Perspective n Angles problem).

PnP проблема

Впервые в современной литературе решение проблемы внешней калибровки камеры c моделью полной перспективы было рассмотрено в 1981 году Фишером и Болсом [1]. Термин "PnP проблема" был введен авторами для задачи определения положения объекта относительно камеры. Условием для решения задачи являются n соответствий между точками изображения и точками модели объекта, а также известное взаимное расположение точек модели объекта.

P1P и P2P проблемы имеют бесчисленное множество решений и поэтому в литературе не рассматриваются. Наибольший интерес представляет P3P проблема, так как для решения этой задачи достаточно лишь трех соответствий между точками изображения и модели. Интерес к данной задаче связан с ее минимальными требованиями к числу найденных соответствий. Дело в том, что выделение черт на изображении и установление соответствия между ними и их проекциями отнимает значительное процессорное время. Следовательно, для приложений, ориентированных на работу в режиме реального времени, требуется использовать минимальное число черт. К сожалению, при точном решении P3P проблемы необходимо решать уравнение четвертой степени. Также возможны такие конфигурации точек, что задача дает 4 различных решения, а выбор единственно верного решения является сложной задачей, требующей большого объема вычислений.

В связи с этим иногда рассматриваются варианты задачи для четырех, пяти и шести точек. Шести точек достаточно для задания системы линейных уравнений, имеющей единственное решение, поэтому PnP проблемы для n больше шести не рассматриваются.

PnL проблема

PnL проблема представляет собой задачу внешней калибровки камеры с условием заданных n соответствий между линиями изображения и линиями (гранями) модели объекта. Ограничения, задаваемые соответствием линий, слабее, чем аналогичные ограничения для точек, так как из первого легко получить второе, выбирая точки парами. К тому же, из произвольного соответствия линий не всегда удается получить соответствие точек, так как линии в пространстве не обязательно пересекаются. С другой стороны, в общем случае линии легче выделить на изображении, нежели характерные точки. Это связано с тем, что для выделения характерных точек требуется поиск черт, коррелирующих с предварительно заданными шаблонами, а для выделения линий достаточно найти лишь градиент интенсивности пикселов изображения.

PnA проблема

PnA проблема – это задача внешней калибровки камеры с условием заданных n соответствий углов между гранями модели объекта и их проекциями на картинную плоскость. В настоящее время имеются решения для двух упрощенных вариантов P3A проблемы. Для первого варианта необходимо, чтобы как минимум два из трех углов модели были острыми. Второй вариант требует, чтобы три угла модели образовывали трехгранный угол.

Способы выбора решения

В связи с тем, что многие методы для задачи внешней калибровки дают множественные решения, возникает проблема выбора из них единственно верного. Существует несколько способов решения данной проблемы:

Для каждого решения из полученного множества строится искусственное изображение посредством проектирования на картинную плоскость черт модели объекта. После этого проводится анализ расположения проекций черт на искусственном и реальном изображениях и делается вывод об истинности решения.
Для каждого решения выполняется проверка ограничений на видимость использованных в методе черт. Если какие-то из этих черт не должны быть видны на изображении при найденном взаимном расположении камеры и объекта, то решение признается недействительным.
В некоторых приложениях задача внешней калибровки решается много раз, например, при переходе от одного кадра к другому. В этом случае, взаимное расположение камеры и объекта не должно изменяться скачкообразно.

Модели камеры

Пусть P некоторая точка трехмерного пространства, а I – ее проекция на картинную плоскость. Путь в некоторой однородной системе координат P описывается вектором [p_x, p_y, p_z ,1]^T, а точке I соответствует вектор [u, v, 1]^T. Тогда общую модель камеры можно описать с помощью 3x4 матрицы M, задающей отображение на картинную плоскость точек трехмерного пространства, попадающих в угол обзора камеры.

λI = MP,

где λ - некоторая константа. Для удобства матрицу М можно представить в виде следующего произведения матриц:

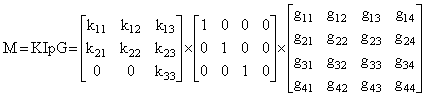(1)

Матрица G определяет переход из координатной системы модели объекта к системе координат камеры. Таким образом, эта матрица содержит информацию о взаимном расположении объекта и камеры, т.е. определяет внешние параметры камеры. Матрица К кодирует внутренние параметры камеры, такие как фокусное расстояние, aspect ratio, начало координат на картинной плоскости. Модель камеры, соответствующей самому общему случаю, когда матрица М может принимать любую возможную конфигурацию, называется моделью проекции. Это модель определяется одиннадцатью параметрами, так как параметр масштаба в однородных координатах значения не имеет. Часто для получения более удобной матрицы модели камеры вводят некоторые ограничения. Например, можно предположить, что матрица внутренних параметров камеры представима в следующем виде:

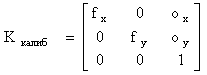, (2)

где f_xи f_y определяют aspect ratio и фокусное расстояние, а o_xи o_y задают начало координат на картинной плоскости. Во многих приложениях эти четыре значения могут быть определены заранее посредством калибровки камеры. Другим важным ограничением является предположение о том, что G задает Евклидово преобразование, получаемое в результате композиции поворотов и параллельных переносов. Модель камеры, учитывающая данные допущения, называется перспективной моделью. Матрица G для такой модели может быть записана следующим образом:

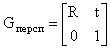, (3)

где R=[r_x, r_y, r_z]^T – это 3х3 ортонормированная матрица, описывающая композицию поворотов для перехода от координатной системы модели к системе координат камеры. Вектор t=[t_x, t_y, t_z]^T представляет параллельный перенос. Для наглядности предположим, что K является единичной матрицей. Пусть вектор p определяет положение некоторой точки P модели объекта в системе координат камеры. Тогда координаты проекции P на картинную плоскость вычисляются по формулам:

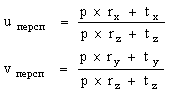, (4)

Таким образом, делители в формулах (4) зависят не только от относительного смещения t_z, но и от смещения по оси Z каждой точки модели – p x r_z. Для того, чтобы избавиться от подобной нелинейности, вводят дополнительные ограничения на матрицу преобразования: предполагают, что М имеет следующий вид:

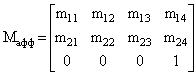, (5)

Модель камеры, соответствующая матрице такого вида, называется афинной моделью. Коордитнаты проекций точек модели объекта линейно зависят от координат p_x, p_y и p_z. Афинная модель является достаточно точной, лишь когда размеры объекта много меньше расстояния от него до оптического центра камеры.

Для некоторых приложений общая афинная модель камеры является слишком сложной (8 параметров). Поэтому вводятся две упрощенных афинных модели камеры: слабая и параллельная перспективы. Различие между ними заключается в том, что модель слабой перспективы – это аппроксимация перспективной модели нулевого порядка, а параллельной – первого.

Рассмотрим выражения (4). Разделим и делитель, и знаменатель каждой дроби на постоянную для всех точек модели величину t_z. Тогда проекции P на картинную плоскость могут быть представлены в виде функций от p:

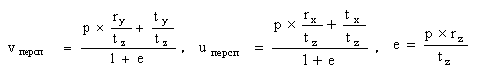Модель слабой перспективы аппроксимирует нелинейную величину 1/(1+e) константой 1, в результате чего имеем:

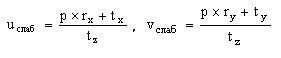Это эквивалентно ортогональной проекции точек модели на плоскость параллельную картинной и сжатию изображения с коэффициентом 1/tz. Модель параллельной перспективы использует приближение первого порядка величины 1/(1+e), то есть:

Такая аппроксимация приводит к следующим формулам:

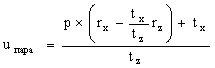Данное отображение эквивалентно проекции точек объекта параллельно линии взгляда на плоскость параллельную картинной. Рисунок 1 поясняет сущность моделей полной, слабой и параллельной перспектив.

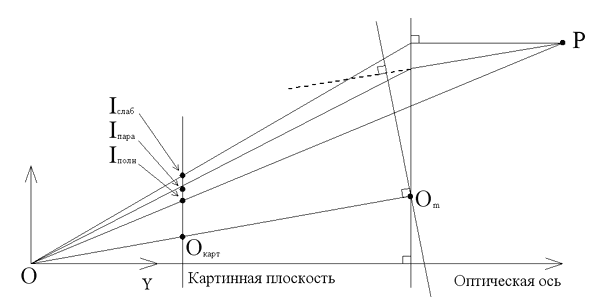
Рисунок 1 – Геометрический смысл полной, слабой и параллельной перспектив

Список использованной литературы

1. Martin A. Fischler, Robert C. Bolles: "Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography". CACM 24(6): 381-395 (1981)
2. William J. Wolfe, Donald Mathis, Cheryl Weber-Sklair, Michael Magee: "The Perspective View of Three Points". IEEE Transactions on Pattern Analysis and Machine Intelligence 13(1): 66-73 (1991)
3. Radu Horaud, Bernard Conio, Olivier Leboulleux, Bernard Lacolle: "An Analytic Solution for the Perspective 4-Point Problem". Computer Vision, Graphics and Image Processing volume 47 pages 33--44 1989
4. Daniel DeMenthon, Larry S. Davis: "Exact and Approximate Solutions of the Perspective-Three-Point Problem". IEEE Transactions on Pattern Analysis and Machine Intelligence 14(11): 1100-1105 (1992)
5. Rodrigo L. Carceroni, Christopher M. Brown: "Numerical Methods for Model-Based Pose Recovery", TR659, Computer Science Dept., U. Rochester, August 1997.
6. P. Ballard, G.C. Stockmann: "Controlling a Computer via Facial Aspect", IEEE Trans. Sys,Man and Cybernetics, 25(4):669-677, 1995.
7. T.D. Alter: "3d pose from 3 corresponding points under weak-perspective projection", Technical Report 1378, MIT Artificial Intelligence Laboratory, 1992.
8. V. Bakic and G. Stockman, "Menu Selection by Facial Aspect", Proceedings of Vision Interface 99, Trois Rivieres, Quebec, CAN (19-21 May 99).