Глеб Кривовязь - Автоматическое сопоставление изображений и облака трехмерных точек

Аннотация

В данной статье рассматривается задача сопоставления изображений и облака трехмерных точек. Предлагается новый алгоритм решения задачи, развивающий существующий подход [11] оценки соответствия между положением камеры и облаком трехмерных точек с помощью максимизации функции взаимной информации фотоизображения и карты глубины. Идея нового метода заключается в одновременном использовании двух изображений сцены. Такой подход позволяет наложить дополнительные ограничения на решение задачи за счет учета геометрических связей между изображениями. Проведенное тестирование показывает улучшение результатов относительно базового метода, что подтверждает перспективность предложенного подхода.

Ключевые слова: сопоставление изображений, облако трехмерных точек, лазерный сканер, параметры внешнего ориентирования камеры, фундаментальная матрица.

ВВЕДЕНИЕ

Все более широкое применение систем лазерного сканирования ставит новые задачи, связанные с обработкой получаемых с их помощью данных – облаков трехмерных точек. Одной из таких задач является сопоставление изображений и облака трехмерных точек некоторой сцены.

Одновременное использование изображений и облаков трехмерных точек открывает новые возможности при анализе сцен. Действительно, эти данные различной природы органично дополняют друг друга, предоставляя информацию как о цвете, так и о трехмерной форме наблюдаемых объектов. Лазерное сканирование и фотосъемка используются совместно, например, при трехмерной реконструкции зданий и построении трехмерной модели местности.

Однако, совместное использование изображений и данных лазерного сканирования эффективно лишь в случае, когда известно точное взаимное расположение соответствующих сенсоров системы в общей системе координат. Но подобная информация, как правило, доступна с недостаточной точностью. Положение и ориентация системы, с которой производится съемка (например, автомобиля или самолета) определяется с помощью датчиков глобального позиционирования (GPS) и инерциальной системы (INS), подверженных сбоям и погрешностям в измерениях. По этой причине актуальной задачей является уточнение взаимного расположения датчиков системы с помощью алгоритмов компьютерного зрения. В литературе данная задача зачастую называется задачей сопоставления (регистрации) изображений и облаков трехмерных точек.

В рамках данной работы задача рассматривается как проблема уточнения положения и ориентации камеры в мировой системе координат при известном положении в пространстве каждой точки облака (т.е. данные лазерного сканирования считаются геопривязанными). Такая постановка задачи характерна для сценария, когда облако трехмерных точек получено заранее и требуется уточнить по нему параметры внешнего ориентирования камеры в процессе фотосъемки.

СУЩЕСТВУЮЩИЕ МЕТОДЫ

Существующие алгоритмы решения рассматриваемой задачи можно разбить на две группы. В первую группу входят методы, основанные на восстановлении разреженного облака трехмерных точек по набору изображений и последующем сопоставлении разреженного и плотного (полученного с лазерного сканера) облаков.

Методы второй группы, напротив, работают с двумерным представлением плотного облака точек - как правило, в виде карт глубины или удаленности - и сопоставляют его с изображениями сцены. Таким образом, задача сводится к задаче сопоставления либо в трехмерном, либо в двумерном пространстве. Рассмотрим методы каждой группы подробнее.

Алгоритмы первой группы, как правило, получают разреженное облако трехмерных точек путем вычисления структуры из движения по набору изображений. Так, в работе [9] авторы используют инкрементальный подход к вычислению разреженной трехмерной модели сцены и метод связок [7] для уточнения параметров камеры и координат трехмерных точек. Сопоставление облаков трехмерных точек производится в два этапа: начальное сопоставление и последующее уточнение регистрации по плоскостям. Недостатком подхода является необходимость пользовательского ввода на этапе начального сопоставления.

В статье [15] авторы используют алгоритм плотного стерео для восстановления трехмерной структуры сцены и метод ICP [16] для сопоставления облаков трехмерных точек. Такой подход требует наличия видеоданных достаточно высокого разрешения, и также не является полностью автоматическим: начальное приближение для метода ICP подбирается вручную.

Некоторые методы напрямую сопоставляют изображения с облаком трехмерных точек. В работе [15] это делается вручную для отдельных кадров видео, тогда как авторы [14] используют алгоритм, основанный на поиске и сопоставлении линейных объектов. Такой подход встречается и в более ранней работе [12], в которой для поиска прямых в облаке точек выполнялась сегментация плоскостей, и находились их пересечения.

Методы второй группы, основанные на сопоставлении в двумерном пространстве, в свою очередь, подразделяются на два типа: использующие геометрические особенности на изображениях и опирающиеся на статистические метрики. К числу первых относится, например, работа [5]. В ней производится сопоставление линий на изображении, найденных с помощью алгоритма [2], и линий на карте глубины. Минусом алгоритма является низкая скорость работы, а также предположение о наличии достаточно числа линий на изображениях. Представляет также интерес работа [8], в которой облако трехмерных точек проецируется на плоскость земли (метод разработан для регистрации изображений и облака точек, полученных с воздуха) и сформированное изображение сопоставляется с бинарным, представляющим собой наиболее характерные участки сцены при съемке сверху. Задача сопоставления формулируется в терминах минимизации энергии.

В отличие от методов, использующих отдельные геометрические особенности, второй тип алгоритмов двумерного сопоставления основан на вычислении некоторой статистики по всему изображению для оценки качества сопоставления. Как подчеркивают в [1], такой подход избавляет от необходимости искать особые точки, линии и прочие характерные элементы, которых может и не быть на изображении. Напротив, статистические методы учитывают также информацию с плоских и однородных участков сцен, таких как крыши, стены, поля и т.д. В [1] в качестве метрики сходства изображений применялась χ²-статистика. Другой распространенной метрикой является взаимная информация, применявшаяся, например, в [3, 13].

Большое значение в контексте данной работы имеет статья [11], авторы которой используют в качестве метрики качества величину взаимной информации между изображением и картой глубины. Отталкиваясь от начального приближения, алгоритм сходится к некоторому решению методом симплексного спуска. Такой подход представляется наиболее перспективным. Он не требует восстановления трехмерных точек по изображению, не подразумевает пользовательского ввода и поиска геометрических особенностей в картах глубины. Однако его недостатком является работа лишь с одним изображением, тогда как обычно доступен целый набор снимков сцены. Целью данной работы является развитие метода [11] на случай использования одновременно пары изображений.

ПРЕДЛОЖЕННЫЙ АЛГОРИТМ

Идея данной работы - использовать подход из статьи [11], добавив в процесс оптимизации второе изображение и изменив оптимизируемую функцию так, чтобы дополнительно учитывать геометрические связи между снимками. Предложенный алгоритм состоит из двух основных шагов:

Поиск соответствующих точек на изображениях. Подчеркнем, что поиск производится один раз до запуска оптимизационного процесса, поскольку изображения не меняются в ходе оптимизации.
Итеративная оптимизация параметров внешнего ориентирования. В отличие от [11], в целевую функцию включается слагаемое, отвечающее за согласованность между фундаментальной матрицей и соответствующими точками, найденными на первом шаге.

Далее рассмотрим каждый шаг подробнее.

Поиск соответствующих точек на изображениях

Для обнаружения соответствующих точек используется стандартная схема сопоставления изображений. Сначала применяется детектор особых точек Харриса [6]. После этого окрестности найденных точек описываются с помощью дескриптора SIFT [10], инвариантного к масштабу и повороту. Соответствия между особыми точками устанавливаются на основе расстояния по дескриптору: для каждой точки первого изображения выбирается ближайшая к ней точка второго изображения. При этом проверяется выполнение и обратного условия. Наконец, ошибочные соответствия удаляются с помощью алгоритма устойчивой оценки параметров RANSAC [4] с фундаментальной матрицей в качестве модели и суммой квадратов расстояний от точек до эпиполярных линий в качестве функции ошибки. Заметим, что фундаментальная матрица, вычисляемая на данном этапе, используется только для оценки правильности найденных соответствий.

Стоит отметить, что выбор уголков Харриса в качестве детектора особых точек обусловлен характером исходных данных – для тестирования в рамках данной работы использовались аэрофотоснимки постоянного масштаба. В случае, например, наземной съемки мог бы потребоваться детектор, учитывающий масштаб. Однако это не повлияло бы на общую схему предлагаемого в работе алгоритма.

Оптимизация параметров камеры

Оптимизация параметров внешнего ориентирования камеры производится итеративно методом симплексного спуска. Целевая функция имеет следующий вид:

F=M(I₁,P₁)+M(I₂,P₂)-λE(I₁,P₁,I₂,P₂) (1)

Здесь M – функция взаимной информации, E – функция ошибки соответствия особых точек, I₁,I₂ - изображения сцены, P₁,P₂ - параметры внешнего ориентирования камеры в мировой системе координат в моменты съемки каждого из двух изображений (более точно, P₁=[R₁,T₁], P₂=[R₂,T₂], где R₁, R₂ - матрицы поворота, T₁, ₂ - вектора смещений), λ - весовой коэффициент.

Аналогично [11], взаимная информация M вычисляется для изображения и карты глубины. Она характеризует степень согласованности (взаимной зависимости) значений яркости и глубины сцены. В [11] показано, что функция достигает своего максимума при правильном положении и ориентации камеры. Подчеркнем, что изображение сцены остается неизменным в процессе оптимизации, однако карта глубины меняется, поскольку зависит от внешних параметров камеры P. Карта глубины строится путем проецирования точек облака на плоскость изображения. Предполагается, что внутренние параметры камеры (фокусное расстояние и координаты принципиальной точки) известны и не меняются, что соответствует большинству практических задач.

Карта глубины представляет собой полутоновое изображение, в котором яркость пикселя кодирует удаленность соответствующей трехмерной точки от камеры (зависимость линейная), см. Рис. 2. Те пиксели, в которые не была спроецирована ни одна трехмерная точка (это возможно при недостаточной плотности облака трехмерных точек), не учитываются при вычислении взаимной информации.

Функция E отражает согласованность между парами соответствующих точек, найденными на первом шаге, и фундаментальной матрицей F, вычисленной по текущим значениям параметров внешнего ориентирования P₁,P₂ (алгоритм вычисления фундаментальной матрицы при известных внешних и внутренних параметрах камеры приведен в [7]).

Пусть x – особая точка на первом изображении, а x′ и l′=x·F – соответствующие ей точка и эпиполярная линия на втором изображении. Расстояние от точки x′ до прямой l′ характеризует согласованность пары точек {x,x′} и фундаментальной матрицы F. Функция E вычисляется как среднее расстояние от точки до эпиполярной линии по всем точкам на обоих изображениях.

Коэффициент λ в формуле (1) необходим для приведения двух метрик различной природы к единому масштабу, он подбирается эвристически. Вопрос определения целевой функции, состоящей из однородных частей, является предметом будущего исследования. Отметим также, что предложенный подход можно рассматривать как одну из вариаций метода связок [7], с измененной целевой функцией. Таким образом, представляет интерес обобщение алгоритма на случай произвольного числа изображений.

РЕЗУЛЬТАТЫ

Тестирование алгоритма производилось на данных аэрофотосъемки (Рис. 1). Критерием качества служил процент успешных сопоставлений. Для каждого изображения были известны правильные значения параметров внешнего ориентирования камеры, поэтому для проверки успешности сопоставления использовался численный критерий (в работе [11] выполнялась визуальная проверка).

Рисунок 1 – Тестовые изображения

Для получения начального приближения в известные значения положения и ориентации камеры вносился случайный шум, что имитировало погрешность работы датчиков GPS и INS. Сопоставление считалось успешным, когда выполнялось следующее условие:

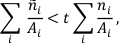
n_i, ñ_i – абсолютные величины отклонений параметра от i правильного значения до и после сопоставления соответственно; A_i – максимальная величина (амплитуда) шума по параметру i; i∈{x,y,z,ω,φ,κ} – три координаты и три угла; t – порог, регулирующий, во сколько раз в среднем стали точнее значения параметров (точность должна возрасти не менее чем в 1/t раз).

При тестировании использовались четыре пары изображений. Для каждой пары тест повторялся 150 раз, для различных начальных приближений. При этом параметры камеры для одного из изображений фиксировались в правильном положении, а для второго – подвергались шуму и оптимизировались. Такой сценарий соответствует ситуации, когда сопоставление для одного из изображений уже было произведено любым из существующих методов, например

[11], и требуется уточнение параметров для остальных снимков. Одновременное уточнение параметров для обеих камер – предмет дальнейшего развития данной работы.

Тест	Успешные сопоставления
Тест	Предложенный метод	Метод [11]
1	57.3%	40.0%
2	58.6%	35.3%
3	45.3%	10.6%
4	50.6%	23.3%

Таблица 1. Результат сравнения предложенного и базового метода

Результаты экспериментального сравнения предложенного и базового метода представлены в Таблице 1. В ходе тестов использовались следующие значения параметров:

A_x=40, A_y=40, A_z=40, A_ω=1, A_φ=1, A_κ=1, t=0.5 .

Значения для координат указаны в метрах, для углов – в градусах. Для весового коэффициента было выбрано значение λ=30.

Как видно из результатов тестов, предложенный алгоритм превосходит базовый метод, что говорит о перспективности идеи данной работы.

ЗАКЛЮЧЕНИЕ

В данной работе был представлен новый алгоритм сопоставления изображений и облака трехмерных точек. Алгоритм развивает один из известных подходов к решению данной задачи [11] на случай нескольких изображений. За счет добавления в процесс оптимизации второго изображения на решение накладываются дополнительные ограничения, обусловленные геометрическими связями между различными снимками одной сцены. Показано, что такой подход превосходит базовый метод по доле успешно произведенных уточнений параметров.

ЗАКЛЮЧЕНИЕ

Работа выполнена при поддержке федеральной целевой программы «Научные и научно-педагогические кадры инновационной России на 2009-2013 годы», контракт №1189.

Список использованной литературы

1. Boughorbal F. Registration and Integration of Multisensor Data for Photorealistic Scene Reconstruction // SPIE Proceedings. 2000. P 74-84.
2. Canny J. A Computational Approach to Edge Detection // IEEE Transactions on Pattern Analysis and Machine Intelligence. 1986. 8. N 6. P 679–698.
3. Collignon A., Maes F., Delaere D., Vandermeulen D., Suetens P., Marchal G. Automated Multimodality Medical Images Registration using Information Theory // Conference on Information Processing in Medical Imaging Proceedings. 1995. 14. P 263-274.
4. Fischler M.A., Bolles R.C. Random Sample Consensus: A Paradigm for Model Fitting with Application to Image Analysis and Automated Cartography // Communications of the ACM. 1981. 24. N 6. P 381-395.
5. Frueh C., Sammon R., Zakhor A. Automated Texture Mapping of 3D City Models with Oblique Aerial Imagery // International Symposium on 3D Data Processing, Visualization and Transmission. 2004. 2. P 396-403.
6. Harris C., Stephens M. A. Combined Corner and Edge Detector // Alvey Vision Conference Proceedings. 1988. P 147–151.
7. Hartley R., Zisserman A. Multiple View Geometry in Computer Vision Second Edition // Cambridge University Press. 2004.
8. Kaminsky R., Snavely N., Seitz S., Szeliski R. Alignment of 3D Point Clouds to Overhead Images // IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops. 2009. P 63-70.
9. Li Y., Low K. Automatic Registration of Color Images to 3D Geometry // Computer Graphics International (CGI). 2009. P 21-28.
10. Lowe D. Distinctive Image Features from Scale-invariant Keypoints // International Journal of Computer Vision. 2004. 60. N 2. P 91-110.
11. Mastin A., Kepner J., Fisher J. Automatic Registration of LIDAR and Optical Images of Urban Scenes // IEEE Conference on Computer Vision and Pattern Recognition. 2009. P 2639-2646.
12. Stamos I., Allen P.K. Geometry and Texture Recovery of Scenes of Large Scale // Computer Vision and Image Understanding. 2002. 88. N 2. P 94-118. 13. Viola P., Wells W. Alignment by Maximization of Mutual Information // International Conference on Computer Vision. 1997. 24. N 2. P 137 -154.
14. Wolberg G., Zokai S. Multiview Geometry for Texture Mapping 2D Images onto 3D Range Data // IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR). 2006. 2. P 2293-2300.
15. Zhao W., Nister D., Hsu S. Alignment of Continuous Video onto 3D Point Clouds // IEEE Transactions on Pattern Analysis and Machine Intelligence. 2005. 27. N 8. P 1305- 1318.
16. Znengyou Z. Iterative Point Matching for Registration of Free-form Curves and Surfaces // INRIA. 1994. 13. N 2. P 119-152.