Моделирование кристаллизации в непрерывной разливке методом конечных точек
Авторы: Lei Zhang, Yi-Ming Rong, Hou-Fa Shen, Tian-You Huang
Перевод: Чирка Д.С.
Источник: Solidification modeling in continuous casting by finite point method
Авторы: Lei Zhang, Yi-Ming Rong, Hou-Fa Shen, Tian-You Huang
Перевод: Чирка Д.С.
Источник: Solidification modeling in continuous casting by finite point method
В данной статье исследуется бессеточный метод конечных точек и рассматривается его применение для моделирования процессов затвердевания металла при непрерывной разливке. Для соответствия вычислений задаче Неймана используется дополнительный параметр. Для расчета скрытой теплоты используется метод энтальпии, представлено соответствующее итерационное решение. Построена итерационная схема для нелинейных вычислений. Модель проверена классической задачей Стефана и методом конечных элементов, затем применена для моделирования роста твердой оболочки при непрерывной разливке на большой площади. Результаты совпали с измерениями.
Непрерывная разливка является одним из наиболее популярных процессов в металлургии. В 2003 г. общий объем металлопродукции Китая составил 2.2 биллиона тонн, и 95.3% от этого объема было выпущено посредством непрерывной разливки. Общая схема процесса разливки представлена на рисунке 1, где жидкий металл заливается из сталеразливочного ковша в промежуточный ковш, затем через погружной разливочный стакан проходит в полость кристаллизатора. Кристаллизатор охлаждается водой настолько, насколько это необходимо для образования твердой корочки необходимой толщины. После этого корочка выводится снизу формы со скоростью разливки, которая соответствует скорости подачи жидкого металла. Для дальнейшего охлаждения слитка по всей его поверхности распыляется вода, и в конечном итоге он полностью затвердевает. Затвердевший слиток выпрямляется, режется и выводится из машины.
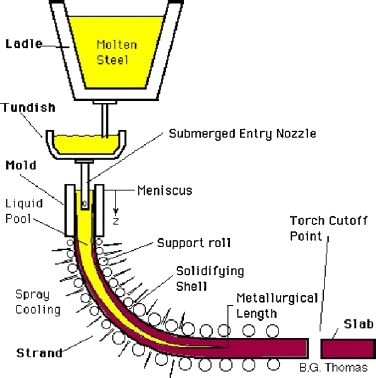
Рисунок 1 – Схема процесса непрерывной разливки
Из-за малой толщины твердой корочки на выходе из кристаллизатора в слитке могут образовываться трещины, которые являются не только основным дефектом, уменьшающим эффективность производства, но и могут привести к несчастным случаям. Возникновение трещин тесно связано с процессами затвердевания в кристаллизаторе. Непрерывная разливка производится при высокой температуре, обычно превышающей температуру плавления стали, что делает невзможным измерение колебаний температур. Так же, физическое моделирование непрерывной разливки требует больших денежных затрат. Для математического моделирования процессов применяются численные методы, основанные, в первую очередь, на методе конечных элементов (МКЭ, FEM).
Однако, составными частями МКЭ являются элементы, и вычисления осложняются обработкой разрывов, т.е. деформаций сетки, не совпадающих с оригинальными линиями сетки. Такие разрывы обычно наблюдаются в задачах крупномасштабных деформаций и прогноза роста трещин произвольными и сложными путями. Решение заключается в перерасчете сетки на каждом этапе эволюции. Но это ведет к снижению точности и росту вычислительной сложности компьютерной программы, нагрузке, связанной с постоянным адаптивным и интерактивным перерасчетом сетки. По сравнению с МКЭ, бессеточный метод не использует элементы. В бессеточном методе аппроксимация строится исключительно в терминах узлов. В результате, разрывы можно обрабатывать посредством добавления или удаления узлов всякий раз, когда необходимо моделирование новых деформаций. Таким образом, можно решать большие классы задач, таких как крупномасштабные деформации и проблемы роста трещины, решение которых с помощью МКЭ являются крайне затруднительным.
Бессеточный метод, называемый так же безэлементным, был разработан около 20 лет назад. Ему предшествовало появление метода гладких частиц (англ. Smoothed Particle Hydrodynamics, SPH), используемый для моделирования астрофизических явлений без границ. Позже Т. Белитчко (Belytschko) разработал безэлементный метод Галеркина (EFG), успешное применение которого вызвало большой исследовательский интерес в направлении бессеточного метода. Так было разработано более десяти бессеточных методов, которым также посвящено несколько книг.
Среди бессеточных методов метод конечных точек (англ. Finite Point Method, FPM) является одним из наиболее простых в реализации и отражающим суть бессеточности. Фактически некоторые бессеточные методы всё же нуждаются в фоновых ячейках, необходимых для оценки интеграции в слабой форме Галеркина. Фоновые ячейки являются обычной сеткой, покрывающей всю область решений. По сравнению с этими методами, метод конечных точек является чисто бессеточным, т.к. он не нуждается в фоновых ячейках. FPM использует только узлы, поэтому он может полностью уйти от перерасчета сеток добавлением или удалением узлов при необходимости обработки разрывов. Это делает FPM эффективным в решении задач крупномасштабных деформаций и роста трещин.
Отличное понимание процессов кристаллизации является основой в решении проблем трещин при непрерывной разливке. Поэтому в данной статье FPM применяется к непрерывной разливке, где с его помощью строится модель кристаллизации. Модель была проверена и использована для моделирования роста твердой оболочки при непрерывном литье большой площади. Результаты совпали с предсказаниями, это свидетельствует о том, что бессеточный метод является потенциальным средством численного анализа и полезен в анализе процессов непрерывного литья.
Метод конечных точек был предложен Е. Онате (Onate).
Краевая задача может быть выражена следующим образом:
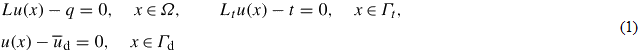
где неизвестная функция u(x) выражает скалярную функцию, такую как температура в решении задачи теплопереноса, или векторную функцию, такую как перемещение, напряжение и деформация в задаче упругости, L и Lt представляют линейные дифференциальные операторы, ud – известное граничное условие на Гd, индексы d и t определяют граничные условия Дирихле и Неймана, q, t, x – переменные.

Рисунок 2 – Схема FPM
В FPM область решений представлена набором узлов или точек коллокации, расположенных в области и на границе, как показано на рисунке 2. В точке i неизвестная функция u(x) аппроксимируется uh(x):

где ψl – функция, полученная методом скользящих наименьших квадратов.
Уравнение (1) выполняется во всех точках подстановкой ур. (2) в ур. (1), получаем:

Уравнение (3) легко программируемо, и т.к. не требуется интегрирования, данный метод намного эффективнее методов, нуждающихся в фоновых ячейках.
Бессеточный метод конечных точек (FPM) изучен в моделировании процессов кристаллизации при непрерывном литье. Модель затвердевания была разработана с помощью:
Модель проверялась на аналитическое решение в одномерном и двумерном случаях. Затем с её помощью был смоделирован рост твердой оболочки при непрерывном литье большой площади. Результаты расчетов совпали с измерениями. Наблюдения показали, что бессеточный метод является потенциальным средством численного анализа и в будущем применим для анализа процесса непрерывного литья с решением задач о трещинах и деформациях.