Реферат по теме выпускной работы
Содержание
- Введение
- 1. Актуальность темы
- 2. Научная значимость работы
- 3. Цель исследования
- 4. Обзор исследований и разработок
- 4.1 Обзор международных источников
- 4.2 Обзор национальных источников
- 4.3 Обзор локальных источников
- 5. Изоморфизм графов
- 6. Инварианты графа
- 7. Результаты магистерской работы
- Выводы
- Примечание
- Список источников
Введение
Теория графов на сегодняшний день активно применяется в химии, информатике и программировании, коммуникационных и транспортных системах, экономике логистике, схемотехнике для решения всевозможных задач. Одной из важнейших и сложнейших задач теории графов является нахождение топологической эквивалентности. Эта задача в той или иной мере неизменно затрагивает все области связанные с теорией графов. Необходимо так же отметить, что на данный момент еще не разработано универсального, качественного и быстрого метода определения топологической эквивалентности вершин графа.
Сложность данной задачи заключается в том, что необходимо определить момент, остановки агента обходящего граф. В связи с этой проблемой представляется невозможным применение генетических и нейросетевых алгоритмов, что значительно усложняет процесс нахождения оптимального решения.
1. Актуальность темы
В настоящее время проблема топологии возникает все чаще и чаще как в программировании, так и в химии. В основном данная задача рассматривается программистами, так как она возникает при программировании движения робота по местности, которому необходимо создать свою карту местности и определить где именно он находится в заданной местности, карта которой дана изначально, либо это другая местность и карту необходимо сохранить. Так же проверку на бисимуляцию активно используют при тестировании, в сетях Петри и LTS. Топология является естественным языком для изучения систем связанных с построением схемы связанности атомов в молекуле.
2. Научная значимость работы
В ходе исследования будет получен алгоритм движения агента по ориентированному графу с помеченными вершинами, который позволит максимально упростить процесс тестирования с использованием LTS, а так же при сравнении сетей Петри на завершающем этапе разработки систем.
3. Цель исследования
Объектом исследования данной работы является изучение существующих на данный момент методик определения топологии, ее недостатки и преимущества. В процессе исследования будут сформулированы базовые гипотезы и законы для разработки метода определения топологической эквивалентности вершин графа. Данный метод позволит разработать программный комплекс который упростит работу химиков, а так же позволит сверять результаты тестирования программных комплексов быстрее и эффективнее.
4. Обзор исследований и разработок
Так как теория графов является неотъемлемой частью тестирования программного продукта, а так же широко применяется при разработке систем разного уровня. Проблемы возникающие с определением бисимуляции вершин графа связаны непосредственно с робототехническими системами, то есть передвижению робота на местности. Эти вопросы широко исследуют американские, европейские и русские ученые, а так же отечественные специалисты в этой области. Вопросам определения топологической эквивалентности вершин графа посвящен ряд работ, в основном, исследователей западной школы.
4.1 Обзор международных источников
В докладе В.М. Бухштабера «Торическая топология» [3] изложены ключевые результаты и приложения торической топологии, как новой области исследований на стыке эквивариантной топологии, комбинаторики многогранников, алгебраической, комплексной и симплектической геометрий, активно развивающейся последние 15 лет. Так же данный вопрос широко освещается Т.Е. Пановым, который занимается разработками в этой области вместе с В.М. Бухштабером [4].
В работе В.А. Башкина представлен метод приближения наибольшей бисимуляции в односчетчиковой сети, основанный на использовании однопериодической символьной арифметики и понятия расслоенной бисимуляции [2].
Определение топологической эквивалентности одного типа локальных особенностей динамических систем было доказано в теореме о топологической эквивалентности в работе С.П. Горбикова «Топологическая эквивалентность одного типа локальных особенностей динамических систем с ударными взаимодействиями» [5].
4.2 Обзор национальных источников
Статья В.П. Пинчука (Запорожский национальный технический университет) посвящена использованию базовых графов для построения топологии многопроцессорных систем. Автор предлагает метод получения полных наборов неориентированных непомеченных графов с заданными свойствами, а О.А. Пришляком (Киевский университет им.Т.Г. Шевченко) предложен метод определения топологической эквивалентности векторных полей Морса-Смейла beh 2 на трехмерных многообразиях [12].
Анализ процессных алгебр и их использование в задачах распределенного имитационного моделирования рассмотрен в работах С.А. Олищук, М.А. Волк (Харьковский национальный университет радиоэлектроники) [11].
4.3 Обзор локальных источников
Статьи Е.А. Пряничниковой посвящены алгебре языков представленной в графах, в них освещаются следующие вопросы:
- «Об алгебре языков, представимых в графах с отмеченными вершинами» в которой рассматриваются свойства алгебры языков, представимых ориентированными графами с отмеченными вершинами [16].
- «Характеризация языков, представимых в графах c отмеченными вершинами» в которой доказывается теорема, аналогичная теореме Майхилла-Нерода для языков, распознаваемых конечными автоматами. На основе доказательства теоремы показано, что любому языку, порождаемому графом с отмеченными вершинами, соответствует единственный с точностью до изоморфизма полный детерминированный граф [15].
- «Алгебры языков, ассоциированные с отмеченными графами« в которой дается определение понятию язык, допустимому в отмеченном графе, вводится система операций на формальных языках [17].
- «О полноте системы аксиом для алгебры языков, представимых конечными ориентированными графами с отмеченными вершинами» в которой разрабатывается система аксиом алгебры языков представленной в графах с отмеченными вершинами и доказывается ее полнота [14].
- «Взаимосвязь алгебр языков, представимых в отмеченных графах» в статье показано что алгебра языков, представимых в графах с отмеченными вершинами, не является алгеброй Клини, и между этой алгеброй и алгеброй регулярных языков нет гомоморфизма [13].
- Совместно с И.С. Грунским изданая статья посвященная алгебре языков, представимых графами с отмеченными вершинами. В которой освещаются свойства алгебры языков, представимых ориентированными графами с отмеченными вершинами [8].
И.С. Грунским, Е.А. Татариновым был предложен метод распознавание конечного графа блуждающим по нему агентом [7]. А так же распознавание лабиринта при помощи конечных автоматов [6]. В соавторстве с Грунским И.С. Сапунов С.В. и Татаринов Е.А. издали статью «Об эксперементах с помечеными графами». В которой проводится эксперемент с агентами взаимодествующими между собой и графом [9].
5. Изоморфизм графов
На рисунке 1 изображены два графа с одним и тем же множеством вершин {a, b, c, d}. При внимательном рассмотрении можно обнаружить, что это разные графы – в левом имеется ребро (a, c), в правом же такого нет. В то же время, если не обращать внимания на наименования вершин, то эти графы явно одинаково устроены: каждый из них – цикл из четырех вершин. Во многих случаях при исследовании строения графов имена или номера вершин не играют роли, и такие графы, один из которых получается из другого переименованием вершин, удобнее было бы считать одинаковыми. Для того чтобы это можно было делать «на законном основании», вводится понятие изоморфизма графов.
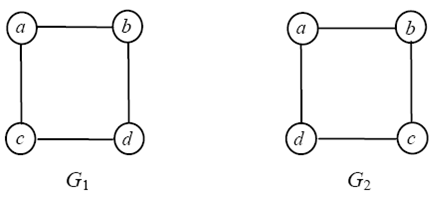
Рисунок 1 – Изоморфные графы
Определение. Графы G1 и G2 называются изоморфными, если существует такая биекция f множества VG1 на множество VG2, что (a,b) ∈ G1 тогда и только тогда, когда (f (a), f (b))∈ G2. Отображение f в этом случае называется изоморфизмом графа G1 на граф G2.
Тот факт, что графы G1 и G2 изоморфны, записывается так: G1 ≅ G2.
Для графов, изображенных на рисунке 1, изоморфизмом является, например, отображение:
x (вершина графа G1): a, b, c, d;
f(x) (вершина графа G2): a, b, d, c.
Заметим, что в этом примере есть и другие изоморфизмы первого графа на второй. Сформулированное определение изоморфизма годится и для ориентированных графов, нужно только обе упоминаемые в нем пары вершин считать упорядоченными.
Изоморфизм – бинарное отношение на множестве графов. Очевидно, это отношение рефлексивно, симметрично и транзитивно, то есть является отношением эквивалентности. Классы эквивалентности называются абстрактными графами. Когда говорят, что рассматриваются абстрактные графы, это означает, что изоморфные графы считаются одинаковыми. Абстрактный граф можно представлять себе как граф, у которого стерты имена (пометки) вершин, поэтому абстрактные графы иногда называют также не помеченными графами [1].
6. Инварианты графа
В общем случае узнать, изоморфны ли два графа, достаточно сложно. Если буквально следовать определению, то нужно перебрать все биекции множества вершин одного из них на множество вершин другого, и для каждой из этих биекций проверить, является ли она изоморфизмом. Для n вершин имеется n! биекций и эта работа становится практически невыполнимой уже для не очень больших n (например, 20! > 2*1018). Однако во многих случаях бывает довольно легко установить, что два данных графа не изоморфны. Рассмотрим, например, графы, изображенные на рисунок 2.
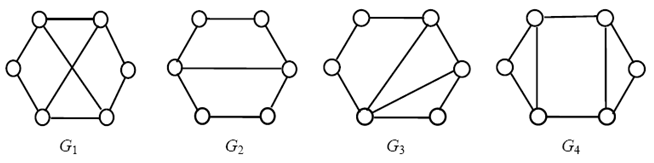
Рисунок 2 – Изоморфные графы
Так как при изоморфизме пара смежных вершин переходит в пару смежных, а пара не смежных – в пару несмежных, то ясно, что число ребер у двух изоморфных графов должно быть одинаковым. Поэтому сразу можно сказать, что графы G1 и G2, у которых разное количество ребер, не изоморфны. У графов G1 и G3 одинаковое число ребер, но они тоже не изоморфны. Это можно установить, сравнивая степени вершин. Очевидно, при изоморфизме каждая вершина переходит в вершину той же степени. Следовательно, изоморфные графы должны иметь одинаковые наборы степеней, а у графов G1 и G3 эти наборы различны. С графами G1 и G4 дело обстоит немного сложнее – у них и наборы степеней одинаковы. Все же и эти графы не изоморфны: можно заметить, что в графе G4 есть цикл длины 3, а в графе G1 таких циклов нет. Ясно, что при изоморфизме каждый подграф одного графа переходит в изоморфный ему подграф другого.
Характеристики графов, которые сохраняются при изоморфизме, называются инвариантами. В этом примере видим некоторые простые инварианты – число ребер, набор степеней, число циклов заданной длины, в дальнейшем будут введены еще многие другие. Если удается установить, что для двух исследуемых графов некоторый инвариант принимает разные значения, то эти графы не изоморфны. Для того чтобы доказать, что два графа изоморфны, необходимо предъявить соответствующую биекцию [10].
7. Результаты магистерской работы
В данной магистерской работе будут рассмотрены и проанализированы существующие алгоритмы определения изоморфизма графов, бисимуляции, трассовой эквивалентности. Целью данной работы является создание более эффективного алгоритма определения топологической эквивалентности и сравнение его с существующими.
Вход: графы G1(s) и G2(t). Графы: ориентированы, без кратных дуг, детерминированы.
Матрицей смежности MATRi заданы графы G1 и G2, исходные вершины s и t, L1 и L2 множество меток вершин графа, Vi(G1,G2), Vn(Gn)-вершины графа, Gn- новый граф, массив новых вершин Smeg(Vn).
Выход: Графы топологичекси эквивалентны или нет.
Метод: Строим Gn(Vn) по ярусам.
Алгоритм.
- Если L(G1)=L(G2) то переходим к 2, иначе к 15. Граф G1 и G2 начинаем исследовать из вершин V1(s0) и V1(t0).
- Если L(s)=L(t), то переходим к 3, иначе к 15.
- 3. Создаем вершину графа Vn и присваиваем ей такой же номер, как и у графа G1 и переходим к 4.
- Построим все смежные вершины Vi(s) и Vi(t). Строим столько ребер сколько букв в алфавите меток. Переходим к 5.
- Если среди полученных результатов будет Vsi=0 и Vti=Vi(t) или Vsi= Vi(s) и Vti=0, то переходим к 15, иначе 6.
- Если лист Vsi=0 и Vti=0 то удаляем поперечные и обратные ребра, и вершину, иначе 7.
- Если листы в графе Gn повторяютcя то переходим к 8, иначе 12.
- Склеиваем вершины Vn(si,ti)=Vn(si,ti) и преходим к 9.
- Сохраняем номера вершин Vsi , Vti и метку вершины L графа G1 в массив новых вершин Smeg(Vn) и переходим к 10.
- Заполняем матрицу смежности MatrGn и переходим к 11.
- Если из Vi нельзя построить новый ярус, то переходим к шагу 12, иначе 4.
- Перемещаемся на ярус назад и проверяем, можем ли из какой либо вершины построить ярус. Если «да» то переходим к 4. Если «нет», то так движемся пока не попадем в начало, и переходим к шагу 13.
- Если G1=Gn переходим к 14, иначе 15.
- Графы топологически эквивалентны.
- Графы топологически не эквивалентны.
В общем виде процесс работы алгоритма показан на рисунке 3.
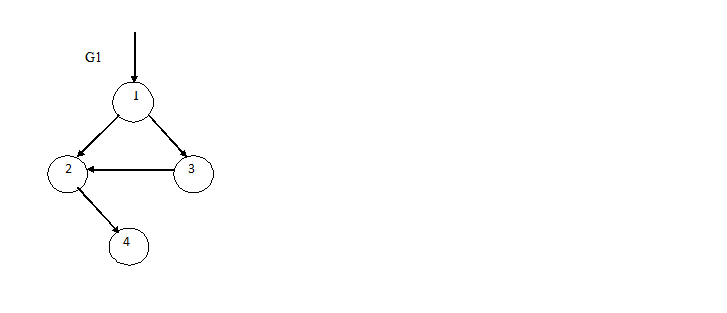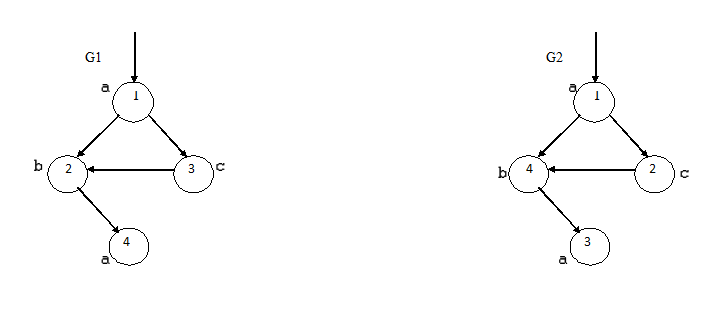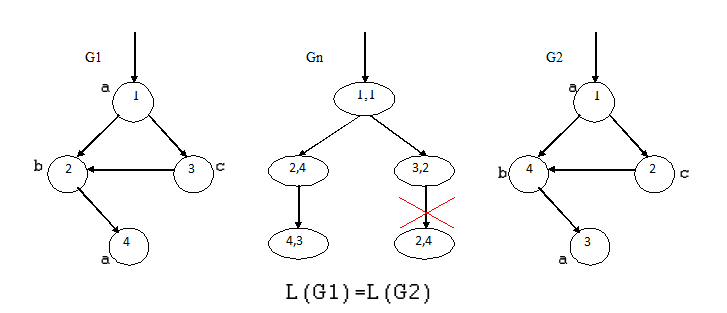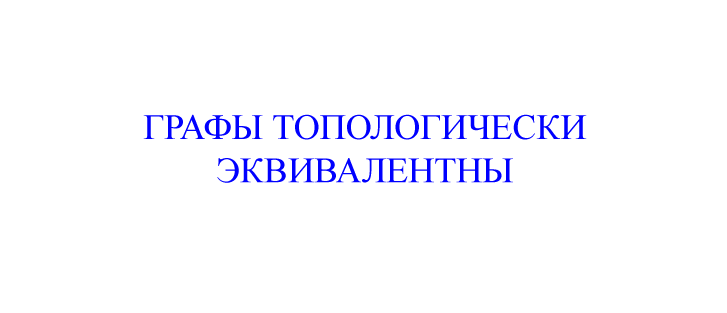
Рисунок 3 – Алгоритм определения топологической эквивалентности
(анимация: 8 кадров, 10 циклов повторення, 30,4 килобайт)
(G1 и G2 – графы, Gn – граф отражающий топологическую эквивалентность G1, G2)
Выводы
Разрабатываемый алгоритм является одним из направлений теории графов, а именно изоморфизм графов и представляет не только теоретико-исследовательский, но и практический интерес. Разработка алгоритма откроет путь к более широкому применению теории графов при проектировании робототехники.
Магистерская работа посвящена актуальной научной задаче объединения основных методов определения изоморфизма графов и алгебры языка разметки. В рамках проведенных исследований получены следующие результаты:
- Исcледованы основные принципы изоморфизма.
- Разработана постановка задачи.
- На основании анализа литературных источников выделены основные алгоритмы, которые могут быть использованы в предложенном подходе к определению биссимуляции деревьев.
Дальнейшие исследования направлены на доработку базовых алгоритмов под заданную спецификацию, определение границ эффективности разработанного алгоритма,проведение математического расчета затрат времени и памяти на реализацию.
Примечание
При написании данного автореферата выпускная работа еще не завершена. Окончательное завершение: январь 2013. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.
Список источников
- Алексеев В.Е. Графы. Модели Вычислительных структур данных / В.Е. Алексеев, В.А. Таланов. – Нижний Новгород. : НижГУ, 2004. – 294 с.
- Башкин В.А. Построение приближений бисимуляции в одноточечных сетях / В.А. Башкин // Труды конференции «Моделирование и анализ информационных систем» – Ярославль: Ярославский государственный университет им. Демидова, 2011. – С. 34–44
- Бухштабер В.М. Торическая топология / В.М. Бухштабер // Общеинститутский семинар « Математика и ее приложения» М : Институт им. В.А. Стеклова, 1990. – 35 с.
- Бухштабер В.М. Торические действия в топологии и комбинаторике / В. М. Бухштабер, Т. Е. Панов – М : МЦ-НМО, 2004. – 272 с.
- Горбиков С.П. Топологической эквивалентности одного типа локальных особенностей динамических систем с ударными взаимодействиями / С.П. Горбиков // Математические заметки, – т.70. – №2. – 2001. – 14 с.
- Грунский И.С. Распознавание лабиринтов при помощи конечных автоматов / И.С. Грунский, Е.А. Татаринов // Труды 4 междунар. конф. «Параллельные вычисления и задачи управления», РАСО’2008, 27–29 октября 2008 г., Москва. – М: ИПУ РАН им. В. А. Трапезникова, 2008. – С. 1483–1498.
- Грунский И.С. Распознавание конечного графа блуждающим по нему агентом / И.С. Грунский, Е.А. Татаринов // Труды 6 междунар. конф. «Параллельные вычисления и задачи управления», РАСО’2009, 27–29 октября 2009 г., Москва. – М: ИПУ РАН им. В.А. Трапезникова, 2008. – С. 483–498.
- Грунский И.С. Об алгебре языков, представимых графами с отмеченными вершинами / И.С. Грунский, Е.А. Пряничникова // Труды Ин-та прикл. математики и механики НАН Украины. – 2009. – т.18. – С. 37–46.
- Грунский И.С. Эксперементы с помечеными графами / И. С. Грунский, С. В. Сапунов, Е.А. Татаринов // Восьмая международная научная конференция «Дискретные модели в теории управляющих систем» М: МГУ 2009. – С. 43–45.
- Москинова Г.И. Дискретная математика / Москинова Г. И. – М.: Логос, 2000. – 198 с.
- Олищук С.А. Базовые графы для построения топологии многопроцессорных систем / С.А. Олищук, М.А. Волк // Конференция «Системы управления, навигации и связи» – Харьков: ХНУР, 2010. – т.16, вып.4. – С.150–158.
- Пинчук. В.П. Базовые графы для построения топологии многопроцессорных систем / В.П. Пинчук // Труды 4 конф. «Искусственный интеллект» – Донецк: ГУИиИИ, 2004. – № 4. – С.46–58.
- Пришляк А.О. Топологическая эквивалентность векторных полей морса-смейла c beh-2 на трехмерных многообразиях / А.О.Пришляк // Успехи математической науки – т.56. – №2. – 2001. – С. 211–212.
- Пряничникова Е.А. О полноте системы аксиом для алгебры языков, представимых ориентированными графами с отмеченными вершинами / Е.А. Пряничникова // Вісник донецького національного університету. Сер. А: Природничі науки. – 2010. – №.1. – С. 259–267.
- Пряничникова Е.А. Характеризация языков, представимых в графах с отмеченными вершинами / Е.А. Пряничникова // Труды Ин-та прикл. математики и механики НАН Украины. – 2010. – т.19. – С. 37–46.
- Пряничникова Е.А. О полноте системы аксиом для алгебры языков, представимых ориентированными графами с отмеченными вершинами / Е.А. Пряничникова // Вісник донецького національного університету. Сер. А: Природничі науки. – 2010. – №.1. – С. 259–267.
- Пряничникова Е.А. Алгебра языков, представимых в отмеченных графах / Е.А. Пряничникова // Theoretical and Applied Aspects of Cybernetics: International Scientific Conference of Students and Young Scientists. – Kyiv. – 2011. – P. 177–179.
