Алгебры языков, ассоциированные с отмеченными графами
В теории конечных автоматов одним из важнейших результатов является теорема Клини, в которой утверждается, что класс языков, распознаваемых конечными автоматами, совпадает с классом рациональных языков, представимых регулярными выражениями алгебры Клини [1].
В данной работе определяется понятие языка, допустимого в отмеченном графе, вводится система операций на формальных языках, которая, в частности, может использоваться в биологии, генетике, а также ДНК – вычислениях [2], и понятие регулярных выражений для этой системы операций.
Исследованы основные свойства семейства алгебр языков, допустимых в отмеченных графах; доказано, что язык допустим в отмеченном графе тогда и только тогда, когда он описывается регулярным выражением во введенной системе операций; разработаны методы анализа и синтеза языков, ассоциированных с отмеченными графами.
Пусть X – конечный алфавит, Х* – множество всех слов конечной длины в алфавите X;Xn – множество всех слов длины n в алфавите X; Х≥n – множество всех слов конечной длины в алфавите X, длина которых больше или равна n.
Определим на множестве Х* частичную бинарную операцию оn склеивания двух слов с параметром n следующим образом: для всех w1, w2∈Х*

РВведем на языках L, R⊆Х* следующие операции
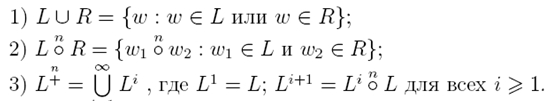
Рассмотрим семейство алгебр (2x+, °n, ∪, +n, ∅, X). В случае, когда n=0, операция °n совпадает с операцией конкатенации, а рассматриваемая алгебра является алгеброй регулярных языков.
Регулярные выражения в алгебре (2x+, °n, ∪, +n, ∅, X) определим следующим образом:1) ∅ является регулярным выражением и представляет язык L(∅)=∅;
2) х является регулярным выражением и представляет язык Ь(х) = {х} для всех
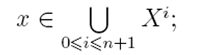
3) если R и Q – регулярные выражения, представляющие языки L(R) и L(Q) соответственно, то выражения (R°nQ), (R∪Q), (R+n) также являются регулярными, причем L(R°nQ) = L(R)°nL(Q), L(R∪Q) = L(R)∪L(Q), L(R+n) = (L{R))+n .
Графом с отмеченными дугами (вершинами) назовем четверку G = (Q, Е, X, μ), где Q – конечное множество вершин; Е⊆Q x Q – множество дуг; X – конечное множе¬ство отметок дуг; μ: Е→X (μ: Q→X) – функция отметок дуг (вершин). Отметкой пути будем называть последовательность отметок входящих в этот путь дуг (вершин).
Пусть I⊆Q – множество начальных вершин графа G с отмеченными дугами или с отмеченными вершинами, F⊆Q – множество финальных вершин. Отметки всех путей в графе G, начальные вершины которых принадлежат множеству I, а конечные – множеству F, назовем языком, допускаемым графом G, и обозначим L(G).
Теорема 1. Язык L⊆Х* допустим в графе с отмеченными дугами (вершинами) тогда и только тогда, когда он описывается регулярным выражением любой алгебры из семейства (2x+, °n, ∪, +n, ∅, X).
Эта теорема в некотором смысле аналогична широко известной теореме Клини для конечных автоматов. В случае, когда n=0 и рассматриваются только графы с отмеченными дугами, теорема 1 совпадает с теоремой Клини. На основе доказательства теоремы разработаны методы анализа и синтеза языков, представимых в отмеченных графах.
СПИСОК ЛИТЕРАТУРЫ
1. Капитонова Ю.В. Математическая теория проектирования вычислительных систем / Ю.В. Капитонова, А.А. Летичевский – М.: Наука, 1988.
2. Anderson J. Automata Theory with Modern Applications / J. Anderson– Cambridge: Cambridge University Press, 2006.
Надійшла до редакції 2011 р.