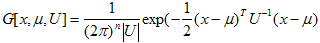Назад в библиотеку
СИСТЕМА ПОФОНЕМНОГО АВТОМАТИЧЕСКОГО РАСПОЗНАВАНИЯ КОМАНД РУССКОЙ РЕЧИ ДЛЯ ПРОИЗВОЛЬНОГО СЛОВАРЯ
OPEN-VOCABULARY HMM-BASED ISOLATED WORD RECOGNITION SYSTEM FOR THE RUSSIAN LANGUAGE
Киселев В.В.(kiselev-v@speechpro.com),
Тампель И.Б.(tampel@speechpro.com),
Татарникова М.Ю.(tatmar@speechpro.com),
Хохлов Ю.Ю.(khokhlov@speechpro.com)
OOO “Центр речевых технологий”, Санкт-Петербург
Автор: Киселев В.В., Тампель И.Б., Татарникова М.Ю., Хохлов Ю.Ю.
Источник: Сайт крупнейшей конференции по компьютерной лингвистике в России.
http://www.dialog-21.ru/digests/dialog2007/materials/html/36.htm
В статье рассматривается способ обучения контекстно-независимых и контекстно-зависимых акустических моделей для русской речи. Приводятся результаты применения полученных акустических моделей в задаче пофонемного распознавания команд.
Ведение
Все задачи, связанные с решением проблемы создания системы распознавания слитной речи с большим словарем, можно разделить на три основные группы. Первая из них связана с анализом речевого сигнала, выделением и моделированием акустических признаков. Вторая отражает зависимости, существующие между словами в языке и определяющими возможные схемы следования слов друг за другом. Наконец, задачи третьей группы связаны с определением наилучшего кандидата на распознавание среди всех возможных с использованием той информации, которая создается в ходе решения задач первых двух групп. На основании такого разделения образуются три основных модуля любой системы распознавания слитной речи: акустическая модель, модель языка и декодер. В данной статье мы остановимся на решении первой задачи: создание акустических моделей для системы распознавания русской речи. В первом разделе статьи описываются методы обработки речевого сигнала и получения признаков. Во втором разделе приводится способ построения акустических моделей. В третьем разделе рассматривается способ получения контекстно-зависимых моделей трифонов. И в четвертом разделе описываются результаты работы системы пофонемного распознавания команд, основанной на акустических моделях, которые позволяют оценить качество полученных разработчиками моделей.
1. Предварительная обработка речевого сигнала и получение признаков.
В качестве предварительной обработки речевого сигнала был выбран набор признаков, известный как MFCC (Mel-Frequency Cepstral Coefficients), который широко применяется в существующих системах распознавания речи. Входной речевой сигнал оцифровывался с частотой квантования 11025 Hz и преобразовывался в последовательность векторов-признаков. Сигнал анализировался с окном 256 отсчетов и шагом 128 отсчетов. На этапе предобработки убиралась постоянная составляющая и выполнялось дифференцирование сигнала для каждого окна, путем применения дифференциального фильтра первого порядка:
где n = 1,N; N – размерность окна;
S(n) – отсчеты речевого сигнала;
k – коэффициент усиления, обычно k = 0.97.
Для ослабления искажений сигнала, вызванных применением к непрерывному сигналу конечного окна анализа, использовалось окно Хэмминга.
Известно, что человеческое ухо воспринимает шкалу частот не линейно вдоль аудио спектра, поэтому анализатор, выполняющий предобработку речевого сигнала в нелинейной шкале, улучшает точность распознавания системы. Моделирование гребенки фильтров происходило с помощью Фурье анализа и суммирования полученных амплитуд спектра сигнала согласно гребенке треугольных фильтров, распределенных в частотной области по шкале Мэл. Обычно используют 20 треугольных фильтров, расположенных равномерно по шкале Мэл от 0 до частоты Найквиста.
Значения амплитуд, получаемые с выходов гребенки треугольных фильтров, сильно коррелируют. Для декорреляции признаков использовалось косинусное преобразование:
где i =1,M; M = 12 – количество кепстральных коэффициентов;
N = 20 – количество фильтров;
mj – логарифм амплитуд с выходов гребенки фильтров.
Кроме 12 кепстральных коэффициентов, в качестве признака добавлялось значение энергии, которое вычислялось на окне анализа:
где Sn – речевые отсчеты сигнала до предобработки;
N – длина окна анализа.
Точность работы системы распознавания увеличивается, если к базовым статическим параметрам добавить временные производные, первую и вторую. Эти производные имеют смысл скорости и ускорения изменения параметров и известны как Delta – коэффициенты и Acceleration – коэффициенты. Delta – коэффициенты вычислялись, с использованием следующей формулы:
Эта же формула, примененная к дельта коэффициентам, позволяет получить Acceleration – коэффициенты.
Таким образом delta и аcceleration коэффициенты вычислялись для всех двенадцати MFCC коэффициентов и энергии. В результате был получен вектор признаков размерности 39, состоящий их 4-х групп признаков:
- Энергия, 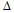 энергии и
энергии и 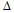
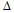 энергии;
энергии;
- 12 кепстральных коэффициентов;
- 12 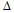 -коэффициентов;
-коэффициентов;
- 12 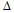
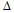 -коэффициентов.
-коэффициентов.
2. Построение акустических моделей.
Акустические модели представляют собой набор скрытых марковских моделей акустических событий, например аллофонов (монофонов или трифонов). Марковской моделью 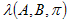 акустического события называется набор из одного или нескольких состояний, характеризующийся следующим набором параметров:
акустического события называется набор из одного или нескольких состояний, характеризующийся следующим набором параметров:
N – количество состояний;
p – начальное распределение вероятностей;
А – матрица переходов из одного состояния в другое;
В – функция плотности вероятности состояния в пространстве признаков или вероятность эмиссии.
СММ могут отличаться топологией: количество состояний модели, разрешенные и запрещенные переходы, возможное направление переходов.
СММ могут отличаться способом задания матрицы вероятностей переходов – A. Вероятности переходов между состояниями могут быть постоянными, а могут зависеть от времени пребывания системы в данном состоянии – такие модели известны как неоднородные (Inhomogeneous Markov Model).
Различают три типа акустических моделей по способу представления функции плотности вероятности – B:
- дискретные;
- полунепрерывные;
- непрерывные.
Для дискретных СММ создается кодовая книга пространства признаков и функция плотности вероятности В представляется Bi(k) – матрицей вероятностей наблюдений кодовых слов для данного состояния, где k – номер слова в кодовой книге, i – номер состояния.
Для непрерывных скрытых марковских моделей, функция плотности вероятности – В для каждого состояния, представляется в виде своего набора M гауссовых функций:
где: x – вектор наблюдений;
Cim – весовой коэффициент, вклад гауссовой компоненты m в функцию плотности вероятности для состояния i;
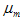 – среднее значение вектора признаков для компоненты гауссовой смеси m;
– среднее значение вектора признаков для компоненты гауссовой смеси m;
Um – ковариационная матрица компоненты смеси m;
G – многомерная гауссова функция:
где: n – размерность вектора признаков;
|U| – детерминант ковариационной матрицы U;
Т – значок транспонирования.
Количество Гауссовых функций М, получаемых для каждого состояния, может, например, контролироваться пороговой функцией, применяемой к энтропии.
Очевидно, что непрерывные СММ обладают чрезвычайно большим количеством оцениваемых параметров и требуют больших вычислительных мощностей. Для преодоления указанной трудности используют метод «связывания Гауссовых смесей» (tied-mixture). В этом случае для всех состояний используется один и тот же набор из M Гауссовых смесей. И для каждого состояния подбираются свои значения весовых коэффициентов Cim. Такие СММ называют еще полунепрерывными моделями. Полунепрерывные модели представляют собой компромисс между скоростью и точностью вычислений.
В представляемой нами системе пофонемного распознавания для акустических моделей монофонов использовалась неоднородная left-to-right СММ без прыжков:
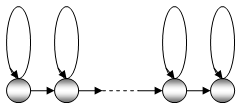
Рис.1. СММ без прыжков
Каждый монофон описывался 1-3 состояниями, в зависимости от длительности монофона и его представительности в обучающей выборке.
Вероятности переходов между состояниями не являются постоянными, то есть используется Неоднородная Марковская Модель (Inhomogeneous Markov Model).
Контекстно-независимые модели представляют собой набор из 59 монофонов и паузы. Для каждого состояния монофона функция плотности вероятности – В представляется в виде своего набора M гауссовых функций.
Для расчета начального набора Гауссовых функций, аппроксимирующих плотности вероятностей состояний в признаковом пространстве, использовалась часть базы данных, прошедшая ручную сегментацию, при этом плотность вероятности для каждого состояния описывалось одной Гауссовой функцией. Увеличение количества Гауссовых функций контролировалось пороговой функцией, применяемой к энтропии. Т.к. вектор признаков первичного описания речевого сигнала состоит из 4-х групп признаков, то наборы Гауссовых функций строились для каждой группы отдельно. Количество гауссовых функций M различно для каждого монофона и каждой группы признаков. Значение M для 1-ого набора признаков, связанных с энергией, в среднем 3-5. Для 2-го, 3-го и 4-го значение М составило 12-15.
3. Построение контекстно-зависимых акустических моделей трифонов.
В настоящее время общепринятым в качестве акустических событий является использование контекстно-независимых фонем (монофонов) для средних словарей и контекстно-зависимых фонем (бифонов, трифонов) для больших словарей. Так называемые контекстно-независимые и контекстно-зависимые акустические модели.
Известно, что в естественной речи речевые органы человека практически никогда не занимают положений, характерных для изолированно произнесенных звуков, а лишь обозначают движение в нужном направлении. Очевидно, что движение в сторону, характерную для данной фонемы, зависит от предшествовавших и, как показывают эксперименты, последующих фонем, то есть, речевой аппарат может готовиться к произнесению некоторых звуков заранее. Этот эффект называется коартикуляцией. Взаимовлияние фонем не ограничивается соседями, а распространяется на несколько соседних фонем. Обычно используют информацию об одном (бифоны) или левом и правом (трифоны) соседях (по аналогии, фонемы без учёта влияния контекста называют монофонами). Различают контексты, зависимые от положения трифона: межсловные трифоны и трифоны внутри слова.
В случае контекстно-зависимых моделей количество фонетических элементов, для которых требуется строить СММ, может достигать нескольких десятков тысяч элементов. Если умножить количество параметров одной СММ, оптимизируемых алгоритмами Баума-Уэлша или Витерби, лежащее в пределах от нескольких сотен до нескольких тысяч, на общее количество СММ, то получится число в несколько миллионов. Такое количество параметров практически невозможно оптимизировать на существующих базах данных и современных компьютерах. Оптимальное множество моделируемых контекстно-зависимых фонов – есть результат компромисса между разрешением и надежностью, и зависит от объёма обучающей выборки.
Существует большое количество методов для сохранения тренированности моделей без принесения в жертву степени разрешения моделей. Основная идея этих методов – связывание функций распределения вероятностей состояний СММ для похожих состояний среди различных моделей фонов. Эта идея используется в большинстве существующих систем, хотя существуют небольшие различия в выполнении и в наименовании результирующих кластерных состояний: senones, genones, PELs, tied-states. Многочисленные способы связывания СММ параметров исследуются для того, чтобы преодолеть проблемы отсутствия данных в обучающих выборках и сократить необходимость использования методов сглаживания распределений [1], [2].
Методы связывания состояний основаны на так называемых методах объединяющей или разделяющей кластеризации. Кластеризация разделяющим решающим деревом [3], [4], особенно интересна, так как алгоритм более быстр в реализации и более надежен, следовательно, более легкий в настройке. Кроме того, связывание СММ состояний основанное на кластеризации решающим деревом, имеет преимущества обусловленные способом построения моделей для невидимых контекстов, т.е. тех контекстов, которые не встречаются в обучающей выборке.
Идея метода заключается в том, что фонемы можно объединить в группы по типу влияния. Например, можно предположить, что согласные с одним и тем же местом образования одинаково влияют на последующую гласную. Тогда несколько трифонов будут описываться одной моделью. Задача метода состоит в использовании объективных критериев для объединения или дробления трифонов и бифонов – построение решающего дерева. Каждой фонеме можно приписать ряд атрибутов, последовательно конкретизирующих её свойства и разбивающих всю совокупность контекстно-независимых фонов (монофонов) на более мелкие классы. Тогда каждый трифон будет являться некоторой конечной ветвью дерева вопросов, поднимаясь по которой мы будем переходить ко всё более широким классам, объединяющим трифоны. Результатом рассматриваемой процедуры будет создание фонетического бинарного «Решающего дерева» (Decision tree), стволом которого является исходный монофон, а конечными ветвями – трифоны, детализированные в той степени, которую позволяют приписанные монофонам атрибуты.
Построенное фонетическое дерево решений позволяет использовать различную степень связанности состояний и, соответственно, различное количество трифонов, удовлетворяя компромисс между точностью распознавания, доступной памятью и быстродействием. Для невидимых трифонов следует использовать наиболее близкую ветвь дерева решений.
В нашей системе для контекстно-зависимых модели функция плотности вероятности – В для каждого состояния, представляется в виде своего набора M гауссовых функций. Один и тот же набор гауссовых функций используется для всех трифонов принадлежащих монофону, стоящему в вершине дерева. В процессе обучения подбираются значения весовых коэффициентов Cim.
4. Тестовые результаты.
Тестирование алгоритмов создания акустических моделей выполнялось на базе данных “Центра речевых технологий”, состоящей из произнесений 252 дикторов: 130 мужчин и 122 женщины. Речевой материал для обучения состоял из 100 предложений для монофонов и 5200 для контекстно-зависимого обучения. Речевой сигнал был записан через стандартный Sound Blaster и микрофон “Sennheiser”, частота дискретизации 22050.
Для тестирования использовался речевой материал, состоящий из произнесений 20 дикторов (10 мужчин, 10 женщин), не входящих в обучающую базу. Дикторы произносили цифры от 0 до 9 и повторяли их два раза. Запись производилась через стандартный Sound Blaster и микрофон “Sennheiser”.
Результаты пофонемного распознавания команд для акустических моделей монофонов и трифонов приведены в Таб. 1. В левом столбце приводится результат правильности распознавания, в правом – процент ошибки.
|
monophone |
triphone |
| Ноль |
100 |
0 |
100 |
0 |
| Один |
100 |
0 |
97,5 |
2,5 |
| Два |
97,5 |
2,5 |
100 |
0 |
| Три |
30 |
70 |
97,5 |
2,5 |
| Четыре |
100 |
0 |
97,5 |
2,5 |
| Пять |
90 |
10 |
90 |
10 |
| Шесть |
97,5 |
2,5 |
100 |
0 |
| Семь |
97,5 |
2,5 |
97,5 |
2,5 |
| Восемь |
100 |
0 |
100 |
0 |
| Девять |
100 |
0 |
100 |
0 |
|
8,8 |
98 |
2 |
91,2 |
Таблица 1. Результаты тестирования
5. Программная реализация
Разработанная система распознавания речи реализована в виде отдельного SDK, включающая динамические библиотеки, заголовочные файлы, примеры использования, демонстрационную программу и документацию. По техническим характеристикам для успешной работы SDK необходимо 100 Mb свободного дискового пространства на жестком диске, не менее 20 Mb оперативной памяти и процессор с частотой не ниже 1кГц.
Демонстрационная программа (Рис. 2) выполнена в виде Win 32 приложения, и предназначена для демонстрации основных возможностей SDK. Пользователю предлагается набрать на клавиатуре распознаваемое слово. Графический, интуитивно понятный интерфейс делает систему простой в и использовании и тестировании работы SDK.
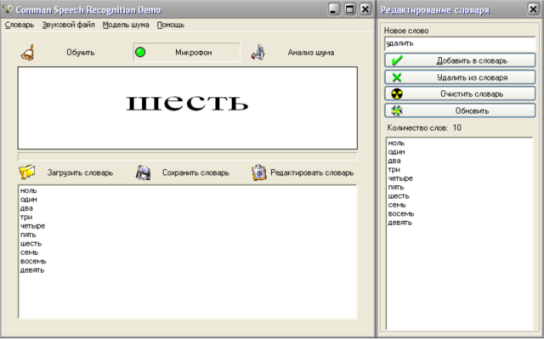
Рис.2. Демонстрационная программа
Список литературы
1. Takahashi S. and Sagayama S., “Four-level tied structure for efficient representation of acoustic modeling”, in Proc.IEEE ICASSP-95, Detroit, MI, May 1995, pp.520-523.
2. Young S.J., “The general use of tying in phoneme-based HMM speech recognizers”, in Proc.IEEE ICASSP-92, San Francisco, CA, Mar. 1992, pp.569-572.
3. Odell J.J. The Use of Context in Large Vocabulary Speech Recognition. Dissertation submitted to the University of Cambridge for the degree of Doctor of Philosophy. 1995.
4. Young S.J., Odell J.J., Woodland P.C., “Tree-Based State Tying for High Accuracy Acousting Modelling”, Proceedings ARPA Workshop on Human Language Technology, Merill Lynch Conference Centre, 1994, pp. 286-291.
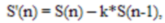
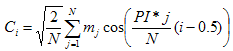
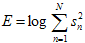
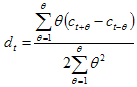
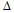 энергии и
энергии и 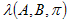 акустического события называется набор из одного или нескольких состояний, характеризующийся следующим набором параметров:
акустического события называется набор из одного или нескольких состояний, характеризующийся следующим набором параметров:
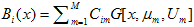
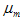 – среднее значение вектора признаков для компоненты гауссовой смеси m;
– среднее значение вектора признаков для компоненты гауссовой смеси m;