Источник: Институт вычислительного моделирования СО РАН, Красноярск, 2000 г., с. 351-372.

МОДЕЛИРОВАНИЕ И ОПТИМИЗАЦИЯ РОБАСТНЫХ ОЦЕНОК ФУНКЦИЙ ПО НАБЛЮДЕНИЯМ

Е. С. Кирик

Институт вычислительного моделирования СО РАН, Красноярск, Россия

e-mail: kirik@icm.krasn.ru

В работе рассматривается цензорный подход к построению и оптимизации робастных оценок функций по наблюдениям и "ремонту" данных. В качестве модели восстанавливаемой неизвестной зависимости принимается непараметрическая оценка регрессии. С целью оптимизации полученной оценки предлагается критерий качества "очистки" выборки.

Введение

Как правило, в обрабатываемых экспериментальных данных в силу различных причин на фоне "типичных", "средних" наблюдений, представляющих собой выборку из некоторой единой генеральной совокупности, содержатся значительные отклонения — "выбросы", "промахи". Среднее количество грубых измерений в данных колеблется около 10-15% [13]. Наличие последних приводит к нарушению условий оптимальности для классических процедур оценивания неизвестных зависимостей по наблюдениям. Задачей теории робастного оценивания является разработка таких процедур, которые позволяют получать высокое качество оценок в этих условиях, но уступают в качестве классическим процедурам при выполнении условий их оптимальности [1]. Термин "робастный" в указанном смысле впервые был введен Боксом в 1953 г. [7].

Чаще всего априорная информация о вероятностных характеристиках "загрязнений" экспериментальных данных и о возможном виде восстанавливаемой зависимости отсутствует. Так же априори неизвестен ни сам факт наличия выбросов, ни наблюдения их содержащие. Поэтому моделировать оценку, устойчивую к выбросам, предпочтительнее в предположении довольно слабых ограничений на саму неизвестную функцию, а так же на данные ее представляющие. Для этих целей наиболее подходит непараметрический подход к анализу данных. С одной стороны здесь в качестве модели неизвестной зависимости рассматривается регрессия, в которой вероятностные характеристики случайных величин заменены их ядерными оценками [10], и следовательно единственным ограничением на функцию является требование ее однозначности. С другой, свойства самих непараметрических оценок и инструмент непараметрической статистики позволяют моделировать робастные оценки цензорного типа и строить критерии оптимальности для этих оценок. Преимущество оценок цензорного типа перед оценками обладающими свойством сглаживания (в первую очередь это непараметрические оценки основанные на минимаксном подходе Хьюбера [9]: [3, 6] и др.) состоит в исключении, точек представляющих выбросы из рассмотрения и, соответственно, исключении влияния последних на оценку. Однако известные цензорные подходы ( [8, 5, 6, 12, 13] и др.) к анализу данных не предполагают этапа проверки качества "очистки" выборки ввиду неформализованности критерия оптимальности, кроме того наличие выбросов в данных является обязательным требованием. Для предлагаемого непараметрического подхода последнее условие не является обязательным, что позволяет получить качество робастной оценки в отсутствии выбросов не уступающее качеству классической непараметрической процедуры оценивания неизвестных функций по наблюдениям.

1. Постановка задачи

Пусть дана обучающая выборка V = {ж;, г/_г}, г = 1, п — статистическая выборка независимых наблюдений (х,у) с помехами случайной величины, распределенной с неизвестной плотностью вероятности р(х,у) и р(х) >0 Vx G х. Считаем, что х = (ж¹, ..., X¹), помехи имеют нулевое математическое ожидание, вид нелинейной стохастической зависимости у = f(x) однозначный. Предполагаем, что выбросы имеют симметричное распределение и могут составлять до 15 % от объема обучающей выборки. Для удобства данные считаются нормированными и центрированными.

*Работа поддержана Красноярским краевым фондом науки, № 10F123N и № 12G188.

© Е. С. Кирик, 2001.

Требуется построить непараметрическую робастную оценку неизвестной зависимости у = f(x) по ее наблюдениям V = {ж;, у;}, г = 1, п.

2. Робастная оценка регрессии

В общем случае (ж₈- = [xj,...,x\)) сходящаяся [4] непараметрическая оценка условного математического ожидания у = f(x) = М(у/х) = f ур(у/х) dy (или регрессии) имеет вид

П I 7 7

Ew

= ' I i ¹-—— • С¹)

ЕП^)

i=ij=i

Оценка (1) получается из (??) подстановкой в нее оценок плотностей типа Розенблата-Парзена ( [11], [10]) с учетом условия самовоспроизводимости Ф(-)

77" f y<I>(V^t)dy = y_l,i = T^,j = Tj. (2)

Чу)

Ф(-) — финитная колоколообразная интегрируемая с квадратом функция, удовлетворяющая условиям 0<Ф(г) <oo,VzeQ(z); -L [ dx = 1;

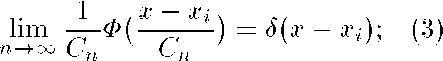
С_п — параметр размытости такой, что

С„ > 0; lim С_п = 0; lim пС^кп = схэ. (4)

п —^ оо п —^ оо

Последний является неизвестным параметром в (1), подлежащим определению. Оптимальный параметр размытости С'_п соответствует минимуму квадратичного критерия оптимальности

п

и²{С_п) = ^2(у(х{) - y_n{xi, С_п)) min (5)

i=1

и находится в ходе скользящего экзамена на обучающей выборке.

Оценка (1) будучи точечной взвешенной оценкой, очевидно, чувствительна к наличию выбросов в данных. Предварительный анализ, предполагающий исследование последних и исключение "подозрительных" элементов из рассмотрения позволяет перейти от непараметрической оценки регрессии (1) к ее робастному аналогу.

Информативным с точки зрения выделения "подозрительных" элементов выборки представляется исследование невязок 6j = yi — y_n(xi),i = l,n И функций ОТ НИХ ( y_n(xi),i = 1 ,п — оценки (1) элементов выборки, вычисленные в режиме скользящего экзамена при оптимальном С_п в смысле критерия (5)). Упорядоченные по возрастанию величины е_г-, г = 1, п образуют вариационный ряд

е¹ < е² < ... < Л (6)

где е¹ = mintj-, е" = maxfj-, г = 1, гг.

На рис. 1 видно, что большей частью они расположены компактно на числовой оси, и лишь некоторые лежат в отдалении от общей массы. Такое распределение невязок обусловлено свойством локальной аппроксимации оценки (1) и свидетельствует о наличии выбросов в выборке. Оценки последних есть взвешенное среднее "хороших" элементов, и, как следствие, они имеют большие по модулю значения невязок. Следовательно, отбросив элементы выборки, соответствующие первым ml и последним т2 элементам

oo о о о ссо о о о

-7 —6 —5 —3 —2 —л. О 1234567S9

Рис. 1. Распределение е,, г = 1, 70

вариационного ряда (6), можно получить робастную оценку регрессии. Возникает вопрос, как определить т 1 и т2, то есть определить выбросы в рабочей выборке. В отсутствии информации о допустимом отклонении оценок элементов V предлагается следующий подход к их дифференциации [2]. Применяя оценку Розенблата-Парзена [10], восстановим функцию плотности невязок е_г , г = 1 ,п

1 ^п —

" 1=1 "

Исследование р_п(е, С'^) на ближайший слева и справа к нулю минимумы (назовем их левым и правым соответственно), позволяет разделить обучающую выборку. Элементы, значения невязок которых лежат между левым и правым минимумами, составят "очищенную" выборку, остальные — выбросы. Таким образом робастная оценка регрессии имеет вид

у_п(х,С_п,С^£п) = ^,-^_Г^-_:-, (8)

i=lj=l

/(•) — индикаторная функция, дифференцирующая элементы выборки,

_Т( ^0; e[a,c]ö[d,b];

1; e (с, d).

а = minjfj}, i = 1, n; b = maxjf,'}, i = 1, n; с = maxjf < 0} : p_n(e, = minVe <0; d = min{f > 0} : p„(e, СД) = min Ve > 0.

з. Оптимизация робастной оценки

Неизвестными в оценке (8) являются параметры размытости С„ и С^. Последний собственно и определяет качество робастизации оценки (8) или качество "очистки" выборки. Для нахождения оптимального значения предлагается следующий критерий

W_Pn = Wl(C_n,C^£n)^mm, (10)

^Сп

где

п

УГ$_п{С_п,С'_п) = (И)

i = l

С'„ — оптимальный.

Таким образом, сначала при каждом фиксированном значении в ходе скользящего экзамена решается задача минимизации (11) по параметру С_п, и затем исследуется на минимум (10).

В основе критерия (10) лежит уже упоминавшееся свойство локальности непараметрической оценки регрессии, которая является чувствительной к качеству наблюдений функции в окрестности восстанавливаемой точки. Чем точнее измерения, тем точнее восстановленное значение функции в точке. С другой стороны, недостаток измерений так же сказывается отрицательным образом на качестве оценки в точках

и, как следствие, на росте величины (11). Причем к изменению С^ в (11) являются чувствительными только слагаемые, соответствующие качественным измерениям восстанавливаемой зависимости. Слагаемые соответствующие выбросам, в силу значительно меньшей доли последних в обучающей выборке, практически инвариантны к значению С^еп и следовательно не определяют изменения значений (11) с изменением С'5..

При известном оптимальном значении С^ нахождение оптимального параметра размытости С_п для "очищенной" выборки состоит в минимизации функционала

п

^WK^Cn) = - - y_n(*i,Cn, Cl))²I(e_uCl) mm . (12)

Tl О _n

i=i

При отсутствии выбросов критерий (10) остается также работоспособным. В этом случае оптимальным является такой параметр С'^, что в категорию выбросов не попадает ни один элемент. Это свойство предлагаемого подхода является довольно ценным, делая предложенный подход устойчивым к возможно ошибочной априорной информации о наличии или отсутствии выбросов в обучающей выборке.

4. Ремонт данных

Под ремонтом данных понимается идентификация и последующая замена грубых измерений (выбросов) значениями робастной модели. Для этого настраивается робастная оценка (8), то есть находятся оптимальные параметры размытости С^ и С„. Затем все выборочные значения, индикаторная функция /(•) которых принимает нулевое значение, заменяются их оценками (8). Для восстановления искомой зависимости по "отремонтированной" выборке можно использовать непараметрическую оценку регрессии (1), где в качестве параметра размытости С„ используется оптимальный для робастной оценки (8).

Заключение

Таким образом предложена непараметрическая робастная оценка регрессии, и алгоритм ремонта данных. Разработанный подход к оптимизации качества "очистки" выборки позволяет говорить об оптимальности последних. Кроме того можно утверждать, что критерий (10) претендует на универсальность и может быть применен для оптимизации любых робастных оценок типа цензурирования с той лишь разницей, что настраиваемым параметром будет не С^ как в данном случае, а параметр соответствующей оценки, отвечающий за качество "очистки" выборки. К достоинствам даннного критерия можно отнести и то, что робастная оценка может быть применена для восстановления зависимостей по слабо зашумленным данным без ущерба для качества относительно обычной оценки.

Проведенное численное исследование предложенного подхода робастизации свидетельствует о высоком качестве получаемых оценок. Представлены результаты работы алгоритма (8), (10), (12) на выборке с выбросами (рис. 2) и без них (рис. 3).

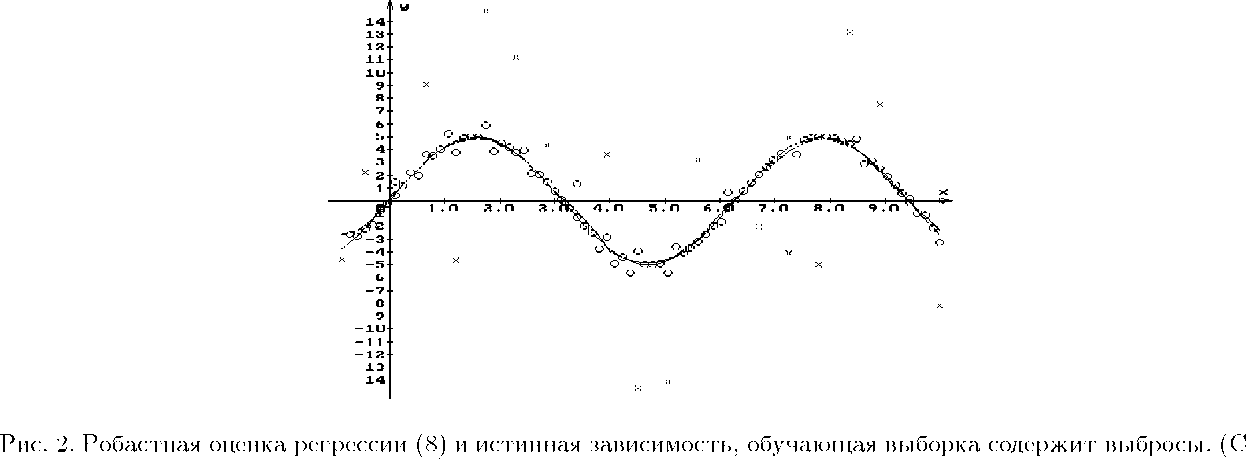
(10) крестики соответствуют выбросам и не не участвуют в вычислениях.)

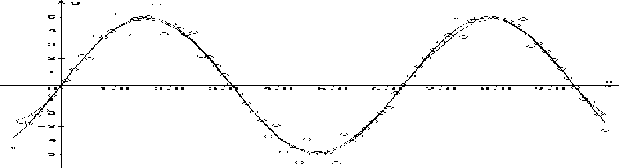
Рис. 3. Робастная оценка 8 и истинная зависимость, обучающая выборка без выбросов

Список литературы

[1] Ершов А. А. Стабильные методы оценки параметров. Обзор. Автоматика и телемеханика. 1978, № 5. С. 66-101.

[2] Кирик-Агапов а Е. С. Об одном подходе к восстановлению и оптимизации робастных оценок функций //Тр. XXXII Региональной молодежной конф. Екатеринбург, ИММ УрО РАН. 2001. С. 31-37.

[3] Катковник В. Я. Непараметрическая идентификация и сглаживание данных. М.: Наука, 1985. 336 с.

[4] Медведев А. В. Непараметрические системы адаптации. Новосибирск: Наука, 1983. 174 с.

[5] Рубан А. И. Методы анализа данных: Учебное пособие. Ч. 1. Красноярск: КГТУ, 1994. 220 с.

[6] Смоляк С. А., Титаренко Б. П. Устойчивые методы оценивания. М.: Статистика, 1980.

[7] Box G. Е. P. Non-normality and tests on variances. Biometrica, 1953, Vol. 40. P. 318-335.

[8] Gorban' A. N., Rossiev A. A. Neural network iterative method of principal curves for data with gaps // J. of Computer and System Sciences International. 1999. Vol. 38, No. 5. P. 825-850.

[9] Huber P.J. Robust statistics: a review. Ann. Math. Statistics, 1972. Vol. 43. P. 1041-1067.

[10] Parzen E. On estimation of probability density function and mode // Ann. Math. Stat. 1962. Vol. 33. P. 1065-1076.

[11] Rozenblatt M. Remarks on some nonparametric estimates of density function // Ann. Math. Stat. 1956. Vol. 27. P. 832-837.

[12] Rousseeuw P. J., van Zomeren В. C. Unmasking multivariate outliers and leverage points //J. of the American Statiscal Association. 1990. No. 85. P. 633-651.

[13] Tukey J. W. The future of the data analysis // Ann. Math. Stat. 1962. Vol. 33, No. 1. P. 1-67.