Оригинал статьи


ЭЛЕКТРОНИКА И ИНФОРМАЦИОННО-ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ                                           ВЕСТНИК ТОГУ. 2009. К» 4 (15)
I*
УДК 004.932
© И. С. Сай, 2009
ЭФФЕКТИВНОСТЬ АЛГОРИТМОВ ПОИСКА ОТТИСКА ПЕЧАТИ В ИЗОБРАЖЕНИИ ДОКУМЕНТА
Сай И. С. – асп. кафедры «Автоматика и системотехника», e-mail: sai@evm.khstu.ru (ТОГУ)
Рассматриваются особенности алгоритмов поиска оттиска печати в изо­бражении документа на основе преобразования Хафа. Приводятся резуль­таты программного моделирования и анализа эффективности базового ал­горитма поиска и модифицированного алгоритма с использование градиен­та яркости.
The article deals with peculiarities in the search algorithm, which uses the Hough transformation, of the impression of a seal in the document image. The results of the program simulation and those of the analysis of effectiveness for the basic search algorithm and the modified one with the use of the brightness gradient are given.
Ключевые слова: преобразования Хафа, алгоритмы поиска, обработка изо­бражений, градиент яркости, программное моделирование.
Введение
Процесс документооборота в современных учреждениях, например в банках, является довольно сложным и трудоемким. Он подразумевает, поми­мо электронного документооборота, который в последнее время выходит на высокий уровень, также бумажный документооборот. Важной задачей в про­цессе обработки бумажных документов является проверка (верификация) подлинности документа. Для проверки подлинности документов существует два вида контроля: подпись уполномоченного представителя и оттиск печати, являющийся уникальным «идентификатором» юридического лица.
Печати и штампы изготовляются специализированными предприятиями с соблюдением определенных требований. Строки текста набираются шриф­том одного размера и рисунка, с одинаковыми интервалами, с симметричным расположением по отношению к разделительным знакам, тексту или рисунку во внутренней рамке. По отношению к центру все буквы текста располагают­ся строго радиально.
В случаях примитивной подделки могут наблюдаться отклонения от этих правил. Оттиски печатей и штампов подделываются путем рисовки, изготов-
53
Т\
ления клише на резине и других материалах, влажной копировки с подлинно­го оттиска, перекопировки через промежуточное клише.
Проверка подлинности оттисков печатей заключается в сравнении от­тиска печати на документе (например, платежном поручении) с печатью ори­гиналом (находится в карточке образцов печатей). Сравнение основывается на принятии решения о том, принадлежит ли печать клиенту, который пре­доставляет платежное поручение, и является ли данная печать подлинной.
В процессе ежедневного документооборота оператору, принимающему документ от клиента, необходимо обрабатывать большое количество доку­ментов и обязательно проверять на подлинность и достоверность каждый принимаемый документ. Для этого операционному работнику необходимо сверять каждый оттиск печати в документе с оттиском образцовой печати. Например, сделаем небольшие расчеты и увидим, что при потоке в 100 доку­ментов в день на одного оператора с учетом того, что проверка одной подпи­си и печати занимает от 30 секунд до нескольких минут, делаем вывод – в день один оператор тратит от 50 до 120 минут только на проверку докумен­тов. Даже при такой проверке оператор не может точно выявить подделки документа, т. к. не является экспертом-криминалистом в данной области. Оператор может выявить только явные несоответствия и вполне вероятно, что не сможет выявить подделку документа.
Учитывая вышеуказанные факторы, можно сделать вывод об актуально­сти исследований в области синтеза автоматизированных экспертных систем проверки подлинности документов.
Выделим основные этапы проверки подлинности печати в документе:
1.    Сканирование и ввод изображения документа в ЭВМ.
2.    Поиск оттиска печати в изображении.
3.    Цифровая обработка изображения печати.
4.    Сравнение с образцом и проверка на подлинность. В данной работе будут рассмотрены особенности алгоритмов поиска от­тиска печати в изображении документа на основе преобразования Хафа.
Базовый алгоритм поиска оттиска печати
Рассмотрим базовый алгоритм поиска оттиска печати в изображении до­кумента, который можно разбить на следующие этапы:
1.    Выделение окрестности содержащей оттиск печати.
2.    Уменьшение масштаба изображения.
3.    Преобразование Хафа.
4.    Поиск максимума в фазовом пространстве.
5.    Вывод изображения печати на экран. При сканировании и загрузки изображения документа выбираем высокое
разрешение сканирования, например в 2496×3507 пикселей.
Полагаем, что в документе, например, в платежном поручении, место­расположение искомой печати является установленным, поэтому проводим поиск не по всему изображению, а внутри предполагаемой окрестности на-54
ЭФФЕКТИВНОСТЬ АЛГОРИТМОВ ПОИСКА
ОТТИСКА ПЕЧАТИ В ИЗОБРАЖЕНИИ                                         ВЕСТНИК ТОГУ. 2009. № 4(15)
ДОКУМЕНТА
I*
хождения печати. Данная окрестность составляет около 40 % от исходного изображения, что позволяет снизить время обработки изображения. В резуль­тате этой операции из исходного изображения размером 2496x3507 выделя­ется окрестность поиска с размером 1248x1169.
На следующем этапе выполняем масштабирование фрагмента по­иска, например с помощью операции усреднения и прореживания пикселей в три раза. В результате этой операции изображение фрагмента с размером 1248x1169 заменяется изображением с размером 416x389.
Основную вычислительную сложность в алгоритме поиска изображения печати представляет преобразование Хафа [1].
Преобразование Хафа позволяет находить на монохромном изображении плоские кривые, заданные параметрически, например: прямые, окружности, эллипсы. Монохромным изображением считается изображение, состоящее из точек двух типов: фоновых точек и точек интереса. Задача преобразования Хафа состоит в выделении кривых, образованных точками интереса.
Идея преобразования Хафа состоит в поиске кривых, которые проходят через достаточное количество точек интереса. Рассмотрим семейство кривых на плоскости, заданное параметрическим уравнением
F(a1,a2...an,x,y) = 0,                                   (1)
где F - некоторая функция, аи а2 ... ап- параметры семейства кривых, х, у -координаты на плоскости. Параметры семейства кривых образуют фазовое пространство, каждая точка которого (конкретные значения параметров аь а2,...ап) соответствует некоторой кривой.
Полагаем, что печать имеет круглую форму и в этом случае геометриче­ское место точек окружности круга можно представить в виде формулы
(х-a)2 +(y-b)2 =R2,                                  (2)
где (а, Ь) - координаты центра окружности, а R - ее радиус, т. е. формула (1), задающая семейство окружностей, имеет вид
F(a,b,R,x,y) = (х-а)2 +(у-Ъ)2 -R2 = 0.                  (3)
Если ставится задача найти окружность заранее известного радиуса, фа­зовым пространством будет плоскость параметров центра окружности (а, Ь).
Если радиус окружности заранее неизвестен, то пространство парамет­ров будет трехмерным - (a, b, R), что существенно увеличивает вычислитель­ную сложность решения задачи. Для сведения задачи обратно к двумерному фазовому пространству в некоторых случаях можно применить метод, опи­санный в [2].
55
Т\
Ввиду дискретности машинного представления входных данных изобра­жения требуется перевести непрерывное фазовое пространство в дискретное. Для этого в фазовом пространстве вводится сетка, разбивающая его на ячей­ки, каждая из которых соответствует набору кривых с близкими значениями параметров. Каждой ячейке фазового пространства можно поставить в соот­ветствие число (счетчик), указывающее количество точек интереса на изо­бражении, принадлежащих хотя бы одной из кривых, соответствующих дан­ной ячейке.
Набор всех счетчиков называется аккумулятором. Любая ячейка задаёт множество кривых, а значение счетчика ячейки определяется количеством точек из пространства (x, y), лежащих хотя бы на одной из этих кривых. Если все точки из (x, y) лежат на одной кривой с фиксированными параметрами, то в соответствующей ячейке значение счетчика будет максимально. Анализ счетчиков ячеек позволяет найти на изображении кривые, на которых лежит наибольшее количество точек интереса.
Заполнение аккумулятора является самой трудоёмкой частью алгоритма, сложность которой зависит от: размерности фазового пространства и сетки дискретизации. Чем больше размерность фазового пространства и меньше сетка, тем больше ячеек в аккумуляторе и, следовательно, больше требуется памяти и времени для его хранения и заполнения.
С целью исследования быстродействия и эффективности базового алго­ритма разработана программа поиска печати в среде Borland C++ Builder 6.0, интерфейс которой показан на рисунке. Отметим основные функции про­граммы: загрузку изображения документа в формате BMP или TIFF; поиск печати на изображении с заданными параметрами поиска; сохранение изо­бражения найденной печати. Программа позволяет выполнять следующие настройки алгоритма поиска: устанавливать следующие коэффициенты мас­штабирования изображения документа 6:1, 4:1, 3:1; обрабатывать несколько файлов с изображением документов; задавать режим фильтрации найденной печати от помех.
Из описания базового алгоритма поиска печати следует, что на время вычисления преобразования Хафа в большой степени влияет коэффициент масштабирования, который задает размер ячейки сетки дискретизации фазо­вого пространства.
В таблице приведены экспериментальные результаты анализа быстро­действия и эффективности алгоритма поиска оттиска печати на основе пре­образования Хафа для разных значений коэффициента масштабирования. Время поиска оценивалось на ПК с процессором Intel Pentium 4 CPU 3.4 GHz. В результате исследований получено, что для обнаружения печатей с вероят­ностью ≈ 90 % достаточно использовать коэффициент масштабирования (6:1), при этом время поиска составляет не более 2 с. Для более точного по­иска с вероятностью ≈ 99 % коэффициент масштабирования должен быть не более (3:1), однако при этом время поиска увеличивается до 35 с.
56
ЭФФЕКТИВНОСТЬ АЛГОРИТМОВ ПОИСКА ОТТИСКА ПЕЧАТИ В ИЗОБРАЖЕНИИ ДОКУМЕНТА
ВЕСТНИК ТОГУ. 2009. № 4 (15)
\$
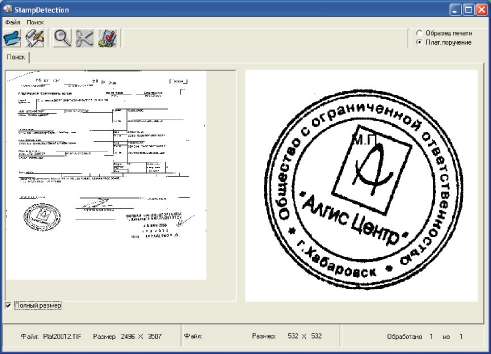
Интерфейсное окно программы поиска печати.
Эффективность базового алгоритма поиска печати.
Коэффициент масштабирования
Среднее время поиска, с
Вероятность обнаружения, %
(6:1)
2
90
(4:1)
13
96
(3:1)
35
99
Модифицированный алгоритм поиска оттиска печати
Из экспериментальных данных, приведенных в таблице, следует, что время поиска оттиска печати при вероятности обнаружения ≈ 99 % является значительной величиной и накладывает временные ограничения на работу автоматизированной системы проверки подлинности документов.
Часто преобразование Хафа применяется к изображениям, полученным операторами выделения краев (края – точки резкого изменения яркости со­седних пикселей) [3]. В таких случаях обычно известно направление градиен­та яркости изображения для каждой точки края [4]. Можно существенно сни­зить количество кривых, потенциально проходящих через заданную точку изображения, если рассматривать только кривые, касательная которой пер-
57
9
ВЕСТНИК ТОГУ. 2009. № 4 (15]
Сай И. С.
пендикулярна градиенту яркости изображения в рассматриваемой точке. Та­ким образом, можно свести задачу выделения окружностей с неизвестным радиусом к двумерному фазовому пространству.
Величину градиента в точке интереса с координатами (x,y) можно вы­числить по следующей формуле:
\АI(x,y)\
(dI
2
(4)
_
dI , ч , ^ , — (x,y) + —(x,y)
dx          ) \dy
где dI / dx – величина градиента в направлении x и dI / dy – величина гра­диента в направлении y.
Направление градиента задается следующим выражением:
dI dI
, dy dx
в = arctan
(5)
Для реализации алгоритма воспользуемся приближенным вычислением градиента (4):
AI(x, y)\ = yj(I(x, y) Ф MX f + (I(x, y) Ф MY )2 ,
(6)
где Ф - операция свертки; MX и MY - матрицы оператора Собеля [5]:
MX =
[-1-2-1]
0    0 0
1    2 1
Г-1 0 1
MY =
2 0 1 0
Алгоритм поиска оттиска печати с использованием градиента яркости можно разбить на следующие этапы:
1. Выделение окрестности, содержащей оттиск печати.
2. Уменьшение масштаба изображения.
3. Вычисление градиента и его направления.
4. Преобразование Хафа.
5. Поиск максимума в фазовом пространстве.
6. Вывод изображения печати на экран. Оценим вычислительную сложность модифицированного алгоритма по
сравнению с базовым алгоритмом. С этой целью выберем простой пример
58
ЭФФЕКТИВНОСТЬ АЛГОРИТМОВ ПОИСКА
ОТТИСКА ПЕЧАТИ В ИЗОБРАЖЕНИИ                                         ВЕСТНИК ТОГУ. 2009. № 4(15)
ДОКУМЕНТА
I*
изображения с размером N х N, в котором точки интереса представляют со­бой окружность заданного радиуса R.
Выполним расчет количества вычислительных операций для базового алгоритма. Для монохромного изображения процесс поиска точек интереса выполняется с помощью операции сравнения всех точек со значением «0» или «1», и этот процесс аналогичен в модифицированном алгоритме.
Так как положение координат центра (а, Ь) окружности заранее неиз­вестно, задаем диапазон изменения координат:
R < а,Ъ < (N - R) .                                       (7)
Для каждой точки интереса с координатами (х, у) при заданных парамет­рах (а, Ь) вычисляем уравнение (3) и, если оно истинно, считаем, что точка принадлежит окружности. Оценим количество вычислительных операций базового алгоритма для каждой точки окружности по следующей формуле:
Мо ={4С± +3Cpow )-(N-2R)2,                         (8)
где С+ - операция суммирования (вычитания); С - операция возведения в
степень.
Для модифицированного алгоритма учитываем операции вычисления градиента (6) и его направления (5), а также изменение диапазона координат центра только в направлении градиента. В результате получим количество вычислительных операций для модифицированного алгоритма:
М1 = (18С+ + Csqrt + Catm) + (4С+ + 3Cpow) • л/2 • (N - 2R),           (9)
где С t - операция вычисления корня; С t - операция вычисления арктан­генса.
Сравнение (8) и (9) показывает, что количество вычислительных опера­ций для модифицированного алгоритма уменьшается пропорционально вели­чине (N - 2R) и зависит от размера окружности.
Следует отметить, что при обработке реальных изображений оттиска пе­чати с целью повышения вероятности обнаружения, зона поиска координат центра печати может быть расширена. В этом случае задается небольшая ок­рестность в направлении градиента и при этом количество вычислительных операций увеличивается.
Алгоритм реализован в виде программы поиска печати в среде Borland C++ Builder 6.0, интерфейс которой аналогичен рисунку. Дополнительно в опции настройки введен выбор алгоритма поиска с использование градиента яркости.
59
Т\
В результате экспериментов получено, что при коэффициенте масштаби­рования (3:1) среднее время поиска составляет не более 1 с. При этом вероят­ности обнаружения ≈ 95 %.
Таким образом, по сравнению с базовым методом использование гради­ента яркости позволяет увеличить быстродействие алгоритма поиска печати примерно в 30 раз. К недостатку алгоритма следует отнести незначительное снижение вероятности обнаружения печати.
В заключение следует отметить, что кроме рассмотренных алгоритмов на основе преобразования Хафа при решении задачи поиска объектов задан­ной геометрической формы можно использовать и другие алгоритмы. На­пример, фрактальные алгоритмы [6] и другие.
Библиографические ссылки
1. Мариничев К., Вежневец В. Алгоритмы выделения параметрических кривых на основе преобразование Хафа // Компьютерная графика и мультимедиа. 2006. № 1(11).
2. Ecabert O., Thiran J-P. Adaptive Hough transform for the detection of natural shapes under weak affine transformations // Pattern Recognition Letters. 2004. № 12(25).
3. Дуда З., Харт П. Распознавание образов и анализ сцен. М., 1976.
4. Сойфера В .А. Методы компьютерной обработки изображений. М., 2003.
5. Гонсалес Р. Цифровая обработка изображений. М., 2005.
6. Перегуда Е. С., Сай С. В. Методы сокращения объема вычислений в алгорит­мах фрактального сжатия изображений // Вестник ТОГУ. 2006. № 1.
60