Назад в библиотеку
Эксперементальная и теоретическая оценки параллельных алгоритмов нахождения минимального остовного дерева на кластерных системах
Автор: Аль-Хулайди А.А., Чернышев Ю.О.
Источник: Информатика, вычислительная техника и инженерное образование. – 2011, № 4 (6), Раздел I, http://digital-mag.tti.sfedu.ru/lib/6/1.doc
Введение
Рассматриваемая задача может найти применение в различных областях:
- Разработка сетей. В данном случае решается задача о соединение n городов в с минимальной суммарной стоимостью соединений.
- Производство печатных плат. По аналогии с сетью, необходимо соединить n контактов проводниками с минимальной суммарной стоимостью.
- Минимальное остовное дерево может использоваться для визуализации многоаспектных, многомерных данных, например, для отображения их взаимосвязи.
Разработка параллельных алгоритмов нахождения минимального остовного дерева и их теоретических оценок, для использования в многопроцессорной среде и в кластерных системах, позволяют достигать значительной величины ускорения, в том числе, и при использовании нескольких тысяч процессоров. В работе [1] приведены теоретические и экспериментальные данные, полученные при выполнении параллельного алгоритма нахождения минимального остовного дерева на
основе метода Прима на кластере, однако отсутствует сколько-нибудь подробное описание параллельного алгоритма нахождения минимального остовного дерева. В данной статье подробно описан параллельный алгоритм нахождения минимального остовного дерева на основе метода Борувки и его теоретическая оценка по сравнение с параллельным алгоритмом Прима, приводятся данные о его производительности, полученные экспериментальным путём.
Постановка задачи
В качестве примера на рис. 1 приведен неориентированный взвешенный граф G, содержащий 8 вершин и 12 ребер. После точки указан целочисленный все ребра.

Рисунок 1 – Взвешенный граф
Последовательный алгоритм Борувки для нахождения минимального остовного дерева приведен в работе [2].
Разработка модификации метода Борувки для параллельных систем
Параллельный алгоритм для нахождения минимального остовного дерева состоит из следующих шагов [3].
Шаг 1 (выбор самого лёгкого). В списке ребер каждой вершины производится поиск самого легкого инцидентного ребра. На рис. 2. показан результат выполнения шага 1 при первой итерации для графа G (см. рис. 1).

Рисунок 2 – Результат поиска самого легкого ребра
Получено 3 дерева с корнями 0,3 и 4 соответственно связные списки выглядят, как показано на рис. 3.
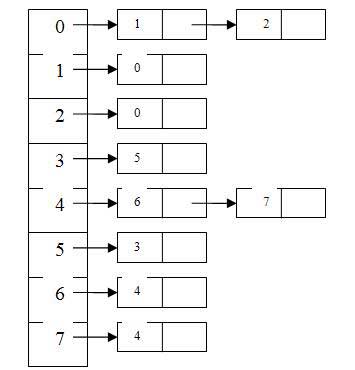
Рисунок 3 – Связный список графа
Шаг 2 (поиск корня). Каждая вершина ищет корень дерева, которому она принадлежит, используя алгоритм подмены указателя. Сначала корень каждого компонента устанавливает свой указатель на себя. Каждая прочая вершина, первоначально указывает на другую конечную точку самого легкого инцидентного ему ребра. Указатели вершин далее обновляются повторяющимися подменами указателя, так, что за одну замену указателя, вершина обновляет свой указатель на равный своего родителя.
Шаг 3 (переименование вершин). Каждый процессор, находит новое имя для всех вершин, находящихся в его списке ребер. Два сообщения – который ей обладает.
Шаг 4 (слияние). Ребра всех вершин компонента, посылаются процессору, который имеет список ребер корня. Список ребер далее сливается процессором.
Шаг 5 (очистка). Каждый процессор, выполняет последовательный алгоритм на своем собственном списке ребер.
В нашей реализации алгоритма подмены указателя на шаге 2 процессоры синхронизируются на каждой итерации цикла.
Рассмотрим шаг 2 алгоритма более подробно.
Время выполнения параллельного алгоритма на шаге 2 значительно больше, чем в последовательной версии.
- Предлагается на шаге 2, использовать пакетную передачу, независимую от количества обновляемых указателей. При условии n<<(n/p), где n – число вершин, а p – количество процессоров, это значительно повысит производительность.
- Новый рандомизированный алгоритм замены указателя.
Детерминистический и рандомизированный алгоритмы, требующие только линейной работы, хорошо известны. Однако они не вполне соответствуют нашей задаче по следующим соображениям: поскольку они предназначены для списков, они требуют соответствующей (линейной) формы входных данных, а не нашей древесной формы с корнем. Путем “линеаризации” дерева можно было бы использовать эти алгоритмы. Но лучше этого не делать, поскольку путь от вершины до корня в компоненте может быть значительно короче в дереве, чем в линейном списке.
Предложена новая схема замены указателей, которая далее будет называться “алгоритмом особых вершин”. Эта рандомизированная схема может быть применена к деревьям и спискам и требует только ожидаемой линейной работы. В первом приближении в нашем алгоритме, каждый компонент обрабатывается следующим образом. Случайным образом выбирается подмножество вершин, называемых “особыми”. Назовем это подмножество SV. Каждая вершина в S-SV выполняет простой алгоритм замены указателя, пока она не укажет на “особую” вершину. В этой точке все вершины, кроме особых, отбрасываются и “особые” вершины повторяют тот же алгоритм рекурсивно (ещё раз с каждой вершиной, случайно выбираемой, как “особая” на следующей итерации). Как только все “особые” вершины указывают на корень, оставшиеся вершины обновляют свои указатели за один шаг так, что они тоже указывают на корень.
Оценки вычислительной сложности параллельного алгоритма Борувки
Ощий анализ вычислительной сложности параллельного алгоритма Борувки для нахождения минимального остовного дерева дает идеальные показатели эффективности параллельных вычислений:
Sp= p и Ep= 1,
где Sp , Ep – соответственно показатели ускорения и эффективности параллельного алгоритма;
n – число вершин в графе G; P – число процессоров.
Для уточнения полученных соотношений введем, в представленные выражения, время выполнения базовой операции выбора минимального значения и, учтем затраты на выполнение операций передачи данных между процессорами. Коммуникационная операция, выполняемая на каждой итерации алгоритма Борувки, состоит в передаче одной из строк матрицы А всем процессорам вычислительной системы. Как показано выше, выполнение такой операции может быть выполнено за log2p шагов. С учетом количества итераций алгоритма Борувки оценка длительности выполнения передачи может быть определена при помощи следующего выражения:
Tp(comm)=n[log2p](r+vn/q),
где r – латентность сети передачи данных, q – пропускная способность сети, v – размер элемента матрицы в байтах.
С учетом полученных соотношений общее время выполнения параллельного алгоритма Борувки может быть определено следующим образом:
Tp=[n/p]*t+ n[log2p](r+vn/q),
где t – время выполнения выбора минимального значения элементарной операции.
Результаты вычислительных экспериментов
Были произведены вычислительные эксперименты для оценки эффективности параллельного алгоритма Прима и разработанного параллельного алгоритма на основе метода Борувки.
Эффективность параллельных алгоритмов проверялись путём выполнения их на кластере следующей конфигурации:
- 4 вычислительных узла (Intel Pentium 4 2,4 ГГц), один узел с двумя процессорами, второй и третий узлы с четырьмя процессорами, четвертый узел с восьмью процессорами;
- управляющий узел (Intel Pentium 4 2,4 ГГц).
Узлы объединены между собой сетью Infiniband (пропускная способность 4 Гбит/с).
Экспериментальные исследования параллельного алгоритма Прима
Результаты вычислительных экспериментов по исследованию параллельного алгоритма Прима представлены в табл. 1, которую иллюстрирует рис. 4.
Результаты экспериментального исследования параллельного алгоритма Прима
Количество вершин, (n) |
Последовательный алгоритм (с) |
Параллельный алгоритм Прима |
2 процессора , p |
4 процессора ,p |
8 процессоров ,p |
Время (с) |
Ускорение (с) |
Время (с) |
Ускорение (с) |
Время (с) |
Укорение (с) |
1000 |
0,0435 |
0,2476 |
0,1757 |
0,9320 |
0,0467 |
1,5735 |
0,0277 |
2000 |
0,2079 |
0,6837 |
0,3041 |
1,7999 |
0,1155 |
2,1591 |
0,0963 |
3000 |
0,4849 |
1,4034 |
0,3455 |
2,2136 |
0,2191 |
3,1953 |
0,1518 |
4000 |
0,8729 |
1,9455 |
0,6220 |
3,3237 |
0,2626 |
5,4309 |
0,1607 |
5000 |
1,4324 |
2,6647 |
0,7363 |
2,9331 |
0,4884 |
4,1189 |
0,3478 |
6000 |
2,1889 |
2,8999 |
0,8214 |
4,2911 |
0,5101 |
7,7373 |
0,2829 |
7000 |
3,0424 |
3,2364 |
1,0491 |
6,3273 |
0,4808 |
8,8255 |
0,3447 |
8000 |
4,1497 |
4,4621 |
1,2822 |
6,9931 |
0,5934 |
10,3898 |
0,3994 |
9000 |
5,6218 |
5,8340 |
1,2599 |
7,4747 |
0,7521 |
10,7636 |
0,5223 |
10000 |
7,5116 |
6,9902 |
1,2915 |
8,5968 |
0,8738 |
14,0951 |
0,5329 |
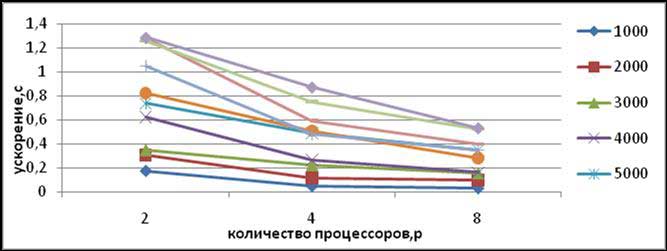
Рисунок 4 – Графики зависимости ускорения параллельного алгоритма Прима от числа используемых процессоров при различном количестве вершин в модели
Результаты экспериментального Т* и теоретического Т исследования параллельного алгоритма Прима приведены в табл. 2.
Результаты сравнения экспериментальной и теоретической оценки времени работы параллельного алгоритма Прима в зависимости от количество вершин в модели при использовании 2 процессоров представлены на рис. 5. Теоретическая оценка проводилась по формуле:
Т=n2[n/p]*+n(r*log2p+3v(p-1)/q+ log2p(r+v/q))
Как видно из табл. 2. и рис. 5, теоретические оценки определяют время выполнения алгоритма Прима с достаточно высокой погрешностью.
Результаты исследования параллельного алгоритма Прима
Количество вершин, n |
Параллельный алгоритм Прима |
2 процессора, p |
4 процессора, p |
8 процессоров, p |
T2, с |
T*2, с |
T4, с |
T*4, с |
T8, с |
T*8, с |
1000 |
0,4054 |
0,2476 |
0,8040 |
0,9320 |
1,2048 |
1,5735 |
2000 |
0,8203 |
0,6837 |
1,6128 |
1,7999 |
2,4120 |
2,1591 |
3000 |
1,2447 |
1,4034 |
2,4264 |
2,2136 |
3,6216 |
3,1953 |
4000 |
1,6786 |
1,9455 |
3,2447 |
3,3237 |
4,8335 |
5,4309 |
5000 |
2,1220 |
2,6647 |
4,0678 |
2,9331 |
6,0479 |
4,1189 |
6000 |
2,5750 |
2,8999 |
4,8957 |
4,2911 |
7,2646 |
7,7373 |
7000 |
3,0375 |
3,2364 |
5,7283 |
6,3273 |
8,4837 |
8,8255 |
8000 |
3,5095 |
4,4621 |
6,5656 |
6,9931 |
9,7052 |
10,3898 |
9000 |
3,9911 |
5,8340 |
7,4078 |
7,4747 |
10,9290 |
10,7636 |
10000 |
4,4821 |
6,9902 |
8,2546 |
8,5968 |
12,1552 |
14,0951 |
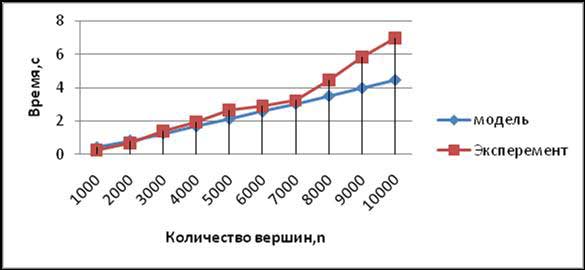
Рисункок 5 – Графики экспериментально установленного времени работы
параллельного алгоритма Прима и теоретической оценки в зависимости от
количества вершин в модели при использовании 2 процессоров
Список использованной литературы
1. Интернет-ресурс http://www.winhpc.ru/?id=138(дата обращения 12.12.2010).
2. Интернет-ресурс http://rain.ifmo.ru/cat/view.php/theory/graph-spanning-trees/mst-2005(дата об-ращения 10.12.2010).
3. Аль-хулайди А.А. Разработка параллельного алгоритма для нахождения минимального остовного дерева // Шестнадцатая международная открытая научная конференция "Совре-менные проблемы информатизации". – Воронеж: Изд-во ВГТУ, 2011. № 3. С.1-14.




