Стефанов А.М. - Дискретная математика

Оптимизация на графах

Граф, каждому ребру которого сопоставлено некоторое число, называется взвешенным графом. Число, сопоставленное ребру, называется весом ребра. Одной из важнейших задач в теории взвешенных графов является задача о кратчайшем соединении, основанная на применении алгоритма Краскала. Рассмотрим это на примере.
Пример.
А,В,С,D,E,F – населенные пункты, линии – проектируемые участки дорог, цифры – их стоимость. Найти, какие дороги надо построить, чтобы полученная схема дорог позволяла попасть из любого города в любой и из всех возможных схем имела наименьшую стоимость.
Решение.

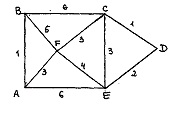
Рисунок 1 – Модель уравнения Ван дер Поля в системе МВТУ

Алгоритм Крускала

1. i – дуга минимального веса из всех имеющихся дуг, не являющаяся петлей.
2. Если дуги m,… к-m уже выбраны, то к выбираем из множества еще не выбранных дуг следующим образом:
а) Добавление дуги к не приводит к образованию циклов;
б) Из дуг, удовлетворяющих условию а, дуга к обладает наименьшим весом.
В нашем случае выбираем 1=CD, 2=АВ, 3=ED и далее отпадает возможность выбора СЕ, т. к. это приводит к образованию цикла. 4=CF и отпадает возможность выбора EF. 5=AF, отпадает возможность выбора BС,BF, AE и процесс выбора дуг автоматически оборвался. Полученный путь изображен на рис. Сплошными линиями.