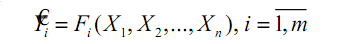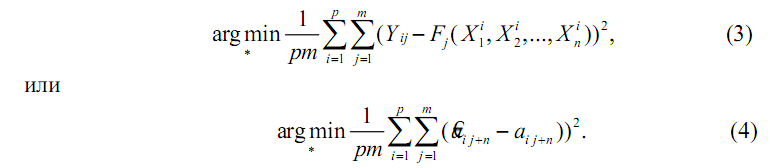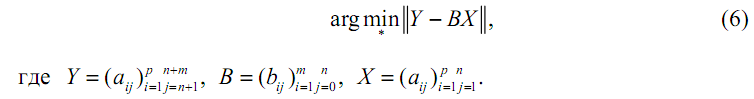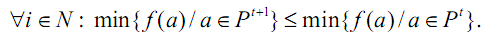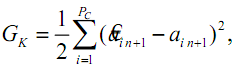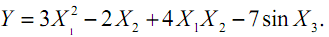Автор:
Снитюк
В.Е.
Источник:
сборниктрудов
VI-й Межд. конф. «Интеллектуальный
анализ информации»,
Киев, 2006, С. 262-271.
Эволюционный
метод восстановления пропусков
в данных
В
статье выполнен анализ моделей и методов, предназначенных для
восстановления отсутствующих данных. Предложен эволюционный
метод, базирующийся на композиции использования нейронной сети
и генетического алгоритма. Технология восстановления пропусков не
требует выполнения ограничений, связанных с линейностью
модели, распределением параметров и других.
Введение
Проблема
обработки и восстановления пропущенных значений в данных свойственна
многим практическим задачам. Чаще всего она возникает при идентификации
зависимостей, априорная информация о значении параметров которых
является неполной. Объективными причинами этого являются
поломки оборудования при измерении значений технических характеристик
процессов, потеря ретроспективной информации, экстремальный
характер функционирования, ограниченный доступ и другие. Субъективные
причины указывают на невозможность получения полной и точной информации
вследствие влияния психологических аспектов и особенностей
памяти.
Адекватная
аналитическая обработка информации с пропусками осложняется из-за
невозможности построения адекватных математических моделей и
их использования для прогнозирования и решения сопутствующих
задач.
Анализ
известных методов восстановления пропусков
Наиболее
распространенными методами обработки неполной информации в
таблицах данных являются такие:
1.
Изъятие
некомплектных строк из таблицы.
Строка или столбец таблицы
данных называется некомплектным, если в нем отсутствует хотя
бы одно значение. Метод применяется при большой размерности
таблицы и незначительном количестве пропусков.В других
случаях метод ведет к смещенности оценок, поскольку строки с
пропущенными значениями содержат новую информацию, необходимую
для анализа.
2.
Заполнение
пропусков средними значениями. В
результате применения такого метода несколько значений одного
фактора оказываются одинаковыми, что указывает на его низкую
точность.
3. Метод
ближайших соседей [1]. Находят
строки таблицы, которые по определенному критерию (обычно, минимума
декартового расстояния), являются ближайшими к строке с
пропуском. Для его заполнения значения фактора у соседей
усредняются с весовыми коэффициентами, обратно
пропорциональными их декартовому расстоянию к строке, которая
содержит пропуск. Метод точнее предыдущего, но он практически
неприменим в случае большого количества пропусков и базируется
на предположении о существовании связей между объектами.
4. Регрессионный
метод [1]. По
комплектным данным строится уравнение линейной множественной
регрессии и вычисляются пропущенные значения факторов. Метод
невозможно применить, если количество пропусков в строке больше одного,
что приводит к множеству решений, и кроме того, в реальных задачах
зависимости, чаще всего, нелинейные, поэтому его точность
является невысокой.
5.
Метод
максимальной правдоподобности и ЕМ-алгоритм [2]. Требует
проверки гипотез о распределении значений факторов. Применение
осложняется в случае большого количества пропущенных значений
фактора.
6.
Алгоритм
ZET [3]. Главная
идея алгоритма заключается в подборе „компетентной
матрицы”, используя данные из которой дальше находят
параметры зависимости, которая используется для
прогнозирования пропущенного значения. Недостатком алгоритма
является его локальность, поскольку для вычисления отсутствующего
значения используются не все данные таблицы, а лишь их часть.
Субъективизм определения размерности „компетентной
матрицы” приводит к учету неинформативных
„шумовых” факторов и смещению оценки неизвестного
значения.
7.
Алгоритм
ZetBraid [3]. Основное
отличие от алгоритма ZET заключается в определении
оптимального размера „компетентной матрицы”. Для
оценки „качества” такой матрицы используется
дисперсионный метод и метод „креста”. Все
другие недостатки, в том числе и статистическая оценка неизвестного
значения исключительно
на основе корреляционно-регрессионного анализа, остаются.
8. Метод
Бартлетта [1]. Неитеративный
метод, который применяется
для заполнения
пропусков в векторе значений результирующей характеристики в
допущении, что значения входных факторов являются
комплектными. Его недостатком является базирование на предположении о
линейной зависимости, но отсутствие обоснования применимости
метода наименьших квадратов приводит к ошибкам.
9. Resampling
[1]. Метод
имеет те же недостатки, что и предыдущий. Он является итеративным и
имеет две модификации. В первой из них некомплектные строки случайным
образом заменяют на комплектные из исходной матрицы и
рассчитывают уравнение регрессии. Во втором варианте уравнение
регрессии получают из комплектной подматрицы, находят оценки
неизвестных значений 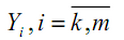 заменяют
пропуски на
заменяют
пропуски на  –
значения ошибок предыдущих
шагов.
Ищут уравнение регрессии. После определенного
количества итераций значения коэффициентов усредняют.
Информационная избыточность на фоне малой мощности множества
комплектных данных в первой модификации resampling и информационная
недостаточность в композиции со случайным формированием значений
исходной характеристики не позволяют получать приемлемые результаты.
Кроме того, отсутствуют процедуры оптимизации метода.
–
значения ошибок предыдущих
шагов.
Ищут уравнение регрессии. После определенного
количества итераций значения коэффициентов усредняют.
Информационная избыточность на фоне малой мощности множества
комплектных данных в первой модификации resampling и информационная
недостаточность в композиции со случайным формированием значений
исходной характеристики не позволяют получать приемлемые результаты.
Кроме того, отсутствуют процедуры оптимизации метода.
10. Моделирование
неполных данных многообразиями малой размерности [4]. Методы,
представляющие данное направление, разработаны учеными
Красноярской школы нейроматематики под руководством проф.
Горбаня О.М. Их главная идея заключается в том, что набор точек, который
является многообразием при наличии пропусков, позволяет строить
линейные и нелинейные приближения - модели, посредством
которых возобновляют пропущенные значения. Результаты алгоритмизации
этих методов и экспериментальных проверок засвидетельствовали
достаточно высокую точность. Проведенные исследования
указывают на удовлетворительное функционирование алгоритма при
10-15% пропусков. В то же время, математические изложения базируются на
достаточно сильных предположениях о распределении входных
данных, гладкости функций и обусловленности матрицы исходных значений.
К недостаткам
следует также отнести сложность реализации и верификации
алгоритма.
Обобщая
результаты анализа рассмотренных методов, делаем вывод об их
низкой точности, наличии жестких требований к исходной информации,
количеству пропусков, размерности матрицы данных, априорных
предположениях о существующих зависимостях, сложности реализации, что
свидетельствует о необходимости разработки методов, базирующихся на
новых парадигмах. В статье предложен метод, интегрирующий в
себе преимущества нейронных сетей для решения задачи идентификации, и
генетического алгоритма для оптимизации.
Постановка
задачи восстановления пропусков
В
общей постановке задача восстановления пропусков в таблицах данных
является такой:
Пусть
X =
(Х1
,Х2,...,Хп)
-
вектор входных факторов Y
= (Y1,Y2,...,Ym)
-
вектор
результирующих характеристик, р
- количество
экспериментов или периодов ретроспективы,
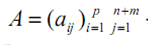 - матрица
исходной информации. Она имеет пропуски, обозначенные
звездочками (табл. 1)
- матрица
исходной информации. Она имеет пропуски, обозначенные
звездочками (табл. 1)
.
Таблица
1. Структура исходной информации
Задача
восстановления пропусков в
данных заключается в нахождении

(1)
где
F =
(F1,F2,...,Fm) и
Y =
(Y1,72,...,
Ym)
-
векторы значений,
полученные по идентифицированным зависимостям
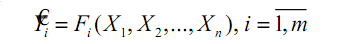 (2)
(2)
и
приведенные в табл. 1, соответственно. Задачу (2) детализируем и
перепишем в виде
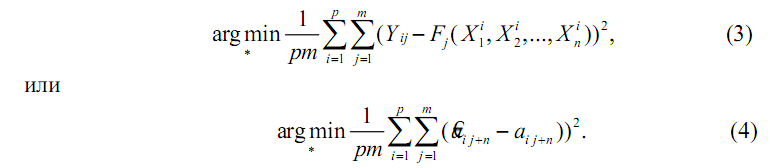 Если
предположить, что зависимости (2)
являются линейными, то есть
Если
предположить, что зависимости (2)
являются линейными, то есть
Y
i = bi0
+bi1X1
+bi2X2
+
...
+ binXn,
(5)
то
задача восстановления пропусков
заключается в нахождении
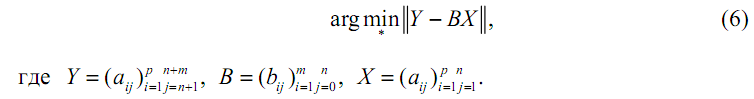 Решение
задач (1)-(6) имеет первый этап, который, в общем случае, заключается в
идентификации зависимостей. Отметим, что в задаче восстановления
пропусков в таблицах данных процедуры идентификации и
оптимизации итеративно повторяются. С некоторыми особенностями
решается задача в зависимости от того, где находятся пропуски:
- только
среди значений входных факторов;
- только
среди значений результирующих характеристик;
- среди значений и
входных факторов, и результирующих
характеристик;
- среди
значений таблицы, в которой входные факторы и
результирующие характеристики не выделены.
Решение
задач (1)-(6) имеет первый этап, который, в общем случае, заключается в
идентификации зависимостей. Отметим, что в задаче восстановления
пропусков в таблицах данных процедуры идентификации и
оптимизации итеративно повторяются. С некоторыми особенностями
решается задача в зависимости от того, где находятся пропуски:
- только
среди значений входных факторов;
- только
среди значений результирующих характеристик;
- среди значений и
входных факторов, и результирующих
характеристик;
- среди
значений таблицы, в которой входные факторы и
результирующие характеристики не выделены.
Предположим,
что пропуски имеются только среди значений входных факторов X
= (Х1,Х2,...,Хп),
результирующая
характеристика Y одна
и существует зависимость
Y
= F(X)
= F(X1,X2,...,Xn).
(7)
А.Н
Колмогоров и В.И. Арнольд доказали теорему [5-7] о том, что
каждая непрерывная функция n переменных, заданная на единичном
кубе n-мерного пространства, представима в виде
где
функции hq(и)
непрерывны, а функции 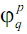 ,
кроме того, еще истандартны, т.е. не
зависят от выбора
функции f . В терминах теории
нейронных
сетей (НС) теорема указывает на то, что любая непрерывная функция
идентифицируема сетью с одним, как минимум, скрытым шаром
нейронов с нелинейными функциями активации. Для идентификации
(7) в качестве модели выберем прямосвязную НС с пороговым алгоритмом
обратного распространения ошибки. Структура сети и ее элементный базис
в экспериментах остается постоянной.
,
кроме того, еще истандартны, т.е. не
зависят от выбора
функции f . В терминах теории
нейронных
сетей (НС) теорема указывает на то, что любая непрерывная функция
идентифицируема сетью с одним, как минимум, скрытым шаром
нейронов с нелинейными функциями активации. Для идентификации
(7) в качестве модели выберем прямосвязную НС с пороговым алгоритмом
обратного распространения ошибки. Структура сети и ее элементный базис
в экспериментах остается постоянной.
Поскольку
входные образы для обучения нейронной
сети имеют пропуски значений, то
необходимо решить задачу параметрической оптимизации. В качестве метода
оптимизации предложено использовать генетический алгоритм (ГА). В
работе [8] доказана теорема:
Пусть
выполнены следующие условия:
1. Последовательность
популяций Р0,Р1,...,...
генерируема ГА, -
монотонна, т.е.
2. Для всех
а, a,
элемент
a
,достижим
из а посредством
мутации и
кроссовера, т.е. через последовательность переходов в ряде
структур Тогда
глобальный оптимум функции /
отыскивается с вероятностью 1:
Если
использовать бинарное представление решений и для формирования
популяции решений - элитный отбор, то теорема указывает на сходимость
ГА по вероятности.
Для
работы ГА необходимо сформировать генеральную и выборочную
совокупность хромосом-решений. Хромосома состоит из
фрагментов, которые отвечают пропускам в таблице данных:
Хr
=<
пропуск 1, пропуск
2,..., пропуск К > .
Данные
в таблице без учета пропущенных значений нормируем. Если в качестве
активационной функции будет использован гиперболический тангенс, то
нормирование предпочтительнее осуществлять в отрезок [-1; 1].
Количество хромосом в генеральной совокупности определяется заданной
точностью результата, в выборочной - исследователем.
На
следующем шаге формируем обучающую и контрольную
последовательность для обучения НС. Предлагается все образы с
пропусками считать элементами обучающей
последовательности. Для
контрольной
последовательности
их использование является проблематичным, поскольку невозможно
использовать для верификации недостоверные значения. Соотношение
мощности множеств образов обучающей и контрольной последовательности
может быть разным, на что влияет соотношение образов с пропусками и без
пропусков в исходной таблице.
Процедура
восстановления пропусков будет такой:
Шаг 1. Инициализация К
хромосом-решений
выборочной последовательности.
Шаг 2. К
= 1.
Шаг
3. Обучение НС на точках обучающей последовательности, где значения
пропусков заполнены значениями К
-й
хромосомы. При этом решается задача поиска
где W
- матрица весовых коэффициентов
НС, Р0
-
количество образов
в обучающей
последовательности.
Шаг 4. Вычисление целевой функции ГА
(fitness-function):
где
Рс
-
количество образов
контрольной последовательности.
Если GK
< Gmin,
то переход на шаг 7.
Шаг
5. К
= К + 1.
Если К>Кmax,
где
Kmax-
количество элементов в
выборочной последовательности, то переход на шаг 6, иначе переход на
шаг 3.
Шаг
6. Выполнение процедур кроссовера, мутации, определение и
отбор хромосом следующей эпохи. Переход на шаг 2. Шаг 7. Вывод
результатов. Конец.
Экспериментальное
моделирование
Для
верификации разработанного метода проведена экспериментальное
моделирование с использованием Matlab 7.0. В качестве
начальных данных для моделирования определены две выборки.
Данные первой выборки сгенерированы искусственно, значения входных
факторов имеют равномерное распределение, а результирующая
характеристика получена по формуле:
Вторая выборка
является официальной статистикой национального информационного
центра энергетики США и содержит данные с 1949 до 2004 года [9],
включающие производство твердого топлива, ядерной и другой энергии,
импорт нефти и других энергоносителей, экспорт угля, газа, кокса и
электроэнергии, потребление твердого топлива, ядерной и другой
энергии, а также общее потребление.
Первая
выборка насчитывала 25 образов, из которых 20 отнесено в обучающую
последовательность и 5 - в контрольную. Моделирование проводилось для
разного количества пропусков при прочих равных условиях. Так,
количество итераций обучения нейронной сети ограничено 50, а
значение целевой функции составило 10. При моделировании установлено,
что такая точность достигнута не была, и процесс обучения
прекращался из-за ограничения на количество итераций. Результаты
приведены в табл. 2, где N - количество пропусков, NP - процентное
соотношения количества пропусков, F - значение целевой функции,
Er-относительная погрешность (в процентах). Зависимость значения
относительной погрешности от количества пропусков изображена
на рис. 1.
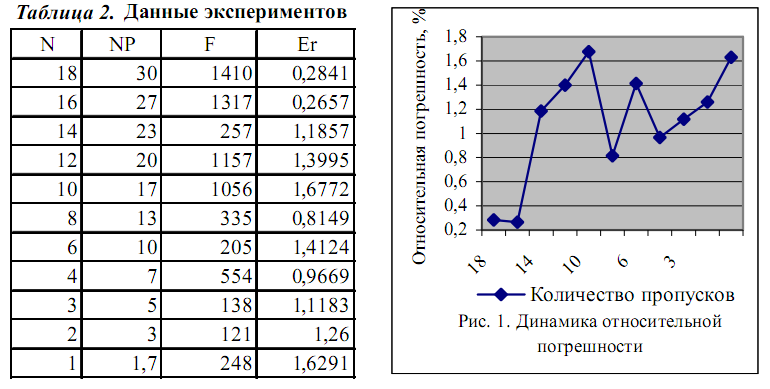
Количество пропусков
Рис. 1. Динамика относительной погрешности
Статистическая
информация, характеризующая состояние энергетики США, состояла
из 11 входных факторов, одной результирующей характеристики и
насчитывала 40 образов. Из них 35 отнесено в обучающую
последовательность и 5 - в контрольную. Количество итераций
установлено 150, значение целевой функции - 1. На второй
выборке итерации прекращались из-за достижения указанного
значения ошибки. Максимальное количество итераций, в отличие от первого
случая, достигнуто не было.
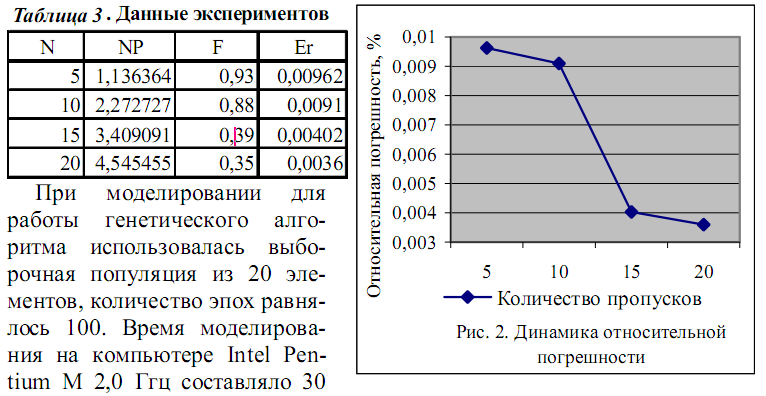
Результаты
моделирования приведены в табл. 3 и на рис. 2.
Заключение
Разработанный
эволюционный метод восстановления пропусков в данных имеет ряд
преимуществ. Так, его использование не требует выполнения ограничений
на исходную информацию. Таблица исходных данных может иметь
произвольную размерность и структуру пропусков.
Перспективным
представляется исследование эффективности использования НС с
неитеративными алгоритмами обучения. Необходимо выяснить влияние
распределения значений факторов на точность восстановления
пропусков.
Как
уже было указано выше, тенденция к увеличению точности идентификации с
ростом количества пропусков также требует своего объяснения. С какой
точностью возможно восстановления пропусков, если их количество
составляет 50% всех значений в таблице данных? Каким условиям должны
удовлетворять значения факторов, чтобы точность
результатов была максимальной? Ответы на эти вопросы позволят
сформировать методику восстановления пропусков с использованием
эволюционного подхода.
Литература
1. Злоба
Е., Яцкие И. Статистические
методы восстановления пропущенных данных //
Computer Modelling & New Technologies. -2002. - Vol. 6.- № 1.
- Pp. 51-61.
2.
Хайкин
С. Нейронные сеты: полный курс.
- М.: “Вильямс”, 2006.
—
1104 с.
3.
Загоруйко Н.Г. Методы
распознавания и их применение. - М.: Сов. радио,
1972. - 216 с.
4. Россиее
А.А. Моделирование данных при
помощи кривых для восстановления пробелов в данных. В кн.
“Методы нейроинфор-матики” / Под ред. А.Н. Горбаня.
- КГТУ: Красноярск, 1998. - С. 6-22.
5. Колмогоров
А.Н. О представлении
непрерывных функций нескольких переменных суперпозициями
непрерывных функций меньшего числа переменных // Докл. АН СССР. - 1956.
- Т. 108.
- №
2. - С. 179-182.
6. Арнольд
В.И. О функциях трех переменных
// Докл. АН СССР. -
1957.
- Т. 114. - № 4. - С. 679-681.
7.
Колмогоров
А.Н. О представлении
непрерывных функций нескольких переменных в виде суперпозиции
непрерывных функций одного переменного // Докл. АН СССР. -
1957. - Т. 114. - № 5. - С. 953-956.
8. Harti
R.E. A global convergence proof
for class of genetic algorithms.- Wien: Technische
Universitaet, 1990. - 136 p.
9.
Annual Energy Report 2004 /
Energy Information Administration USA:
Washington, 2004. - 435 p. http://www.eia.doe.gov/aer
10. Люгер
Ф. Док. Искусственный
интеллект. Стратегии и методы решения сложных проблем. -
М.: “Вильямс”, 2003. - 864 с.
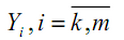 заменяют
пропуски на
заменяют
пропуски на  –
значения ошибок предыдущих
шагов.
Ищут уравнение регрессии. После определенного
количества итераций значения коэффициентов усредняют.
Информационная избыточность на фоне малой мощности множества
комплектных данных в первой модификации resampling и информационная
недостаточность в композиции со случайным формированием значений
исходной характеристики не позволяют получать приемлемые результаты.
Кроме того, отсутствуют процедуры оптимизации метода.
–
значения ошибок предыдущих
шагов.
Ищут уравнение регрессии. После определенного
количества итераций значения коэффициентов усредняют.
Информационная избыточность на фоне малой мощности множества
комплектных данных в первой модификации resampling и информационная
недостаточность в композиции со случайным формированием значений
исходной характеристики не позволяют получать приемлемые результаты.
Кроме того, отсутствуют процедуры оптимизации метода.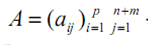
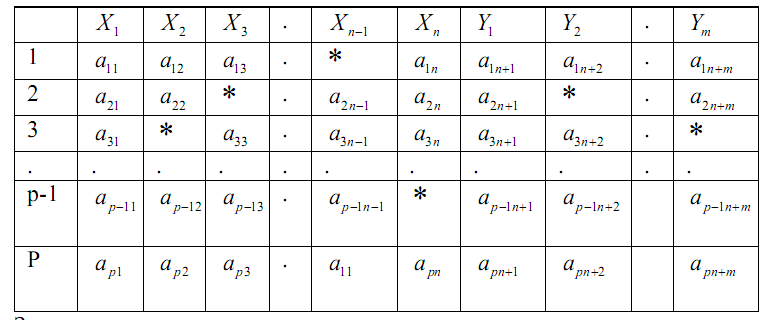
 (1)
(1)