Рассмотрена задача целенаправленной предобработки обучающей выборки для ускорения обучения нейросети. Индикатором сложности выборки служит значение константы Липшица выборки. Для базы реальных данных, линейной и нелинейной предобработок независимых признаков показана зависимость свойств обученных нейронных сетей от величины константы Липшица выборки.
The problem of optimal data preprocessing for faster neural network training is explored. The value of Lipschitz constant estimated over training set is taken as a measure of training set complexity and preprocessing scheme goodness. Several preprocessing schemes and tricks are tested over the real world database and close relation between training set Lipschitz value and neural network properties is obtained.
Методы предобработки данных
Предобработка данных является важным шагом при применении обучаемых с учителем нейросетей [1,2] и определяет скорость обучения величины ошибок обучения и обобщения и иные свойства сети. Здесь будет рассмотрена только предобработка количественных признаков. Схемы предобработки качественных признаков даны в [1]. Для предобработки количественных величин чаще всего применяют линейный сдвиг интервала значения признака, например, в интервал [-1,1]. Формула пересчета значения признака x для i-го примера выборки в интервал [a,b] такова:
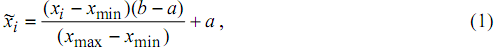
где xmin, xmax
- минимальное и максимальное
выборочные значения признака.
При отсутствии жестких ограничений на диапазон значений предобработанного признака может быть выполнено масштабирование, дающее нулевое среднее и единичную дисперсию предобработанной величине, по формуле:
При отсутствии жестких ограничений на диапазон значений предобработанного признака может быть выполнено масштабирование, дающее нулевое среднее и единичную дисперсию предобработанной величине, по формуле:
где
M(x),
σ(x)
- исходное
выборочное
среднее и среднее квадратичное
отклонение.
Получение нулевых средних для входных сигналов сети ускоряет градиентное обучение, поскольку снижает отношение максимального и минимального ненулевого собственных чисел матрицы вторых производных целевой функции по параметрам сети [3,4].
Иногда проводят и предварительную (перед линейным масштабированием) нелинейную предобработку - например, логарифмирование. При одновременном же рассмотрении всего набора независимых признаков можно убрать линейные корреляции между признаками, что также положительно влияет на скорость обучения [3,4].
Настоящая работа лежит в рамках специализированного подхода по построению предобработки путем привлечения информации и об отдельных "знаковых" примерах выборки. Примером подобной идеологии может служить работа [5], где для получения робастности к выбросам в независимых переменных кластеризуются данные обучающей выборки, и каждая статистически достоверно вылетающая за типичный радиус разброса для своего кластера точка (пример) проецируется по направлению к центру кластера.
Идея минимизации выборочной константы Липшица
На практике при предобработке данных обычно не оценивается получаемая в итоге "сложность" обучающей выборки для нейронной сети. В [1,2] предложено оценивать значение константы Липшица (далее КЛ) обучающей выборки. КЛ выборки
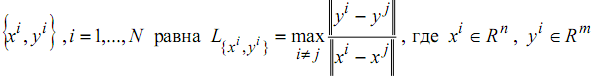- вектора
входных
сигналов и требуемых выходныx сигналов нейросети.
Показано [6], что КЛ выборки влияет на процесс обучения и свойства обученной сети, и при предобработке выборки нужно минимизировать КЛ. Здесь результат [6] расширен в плане обсуждения и сравнения с иными стратегиями предобработки.
Поскольку КЛ выборки определяется примерами с разными ответными и близкими входными частями, то целенаправленно предобрабатывать нужно входные признаки, имеющие различные значения для этих конфликтных примеров.
Для снижения КЛ в [1,2] даны схемы предобработки количественного признака путем преобразования его в бόльшее число переменных. Однако, эти схемы не дают нулевые средние значения получаемых величин ñ каждую из последних может потребоваться дополнительно центрировать и масштабировать.
Расчет КЛ требует порядка (n+m)N2 операций, где N, n, m - число примеров выборки, входных и выходных сигналов сети соответственно. Современные ПК вычисляют КЛ выборок n+m ≈ 100/200 и N ≤ 50000 за минуты/десятки минут. Обучение нейросетей при этом требует бoльшего или сопоставимого времени.
При непересекающихся классах возможно обучение на малом предварительно отобранном наборе наиболее близких друг к другу примеров разных классов - примеров, между которыми и должна проходить разделяющая поверхность [7,8]. Эту идею можно применять и для уменьшения числа примеров, участвующих в расчете КЛ, так как при трансформации признака любым монотонным отображением R → R отобранные примеры по прежнему будут располагаться вдоль границы решения. Поэтому становится возможен быстрый неоднократный расчет КЛ на отобранном меньшем числе примеров с целью целенаправленного подбора уже самих способов предобработки из класса монотонных функций. Однако, задача прогноза либо иные методы active pattern selection (как метод [9] минимизации ошибки обобщения путем динамической селекции обучающих примеров) не позволяют предварительно отбирать малое число примеров.
Исходные данные для экспериментов и использованные алгоритмы
Взята известная база данных Statlog NASA Shuttle [10,11]: 43500 обучающих и 14500 тестовых примеров, 9 количественных входных признаков, классификация на 7 классов (при очень неравномерном распределении примеров по классам). Использовался авторский нейроимитатор NeuroPro, выбранные алгоритмы и стратегии были таковы:
• Взяты сети со скрытым слоем из 15 нейронов с сигмоидами f(x)=x/(0.1+|x|) и линейными выходными нейронами. Синапсы изначально равномерно распределены в [-0.1,0.1] и при обучении не ограничиваются. Для каждого способа предобработки выборки обучались копии 20-ти первоначально сгенерированных нейросетей.
• Для обучения брались все примеры обучающей выборки, на тестовой выборке выполнялось только тестирование обученных сетей. Использовался метод сопряженных градиентов в пакетном (batch) режиме с оптимизацией шага.
• Использовалась специальная классификаторная целевая функция из [1], веса классов установлены обратно пропорционально числу примеров в классе.
• Обучение прерывалось при распознавании правильно и с заданной надежностью 99% примеров обучающей выборки. Реально при этом правильно, но может быть с недостаточной надежностью, классифицировалось 99.7-99.9% примеров выборки.
• Обученные сети на тестовой выборке давали >99.6% правильных ответов. При обучении не использовались приемы увеличения обобщающей способности сетей.
Целенаправленная минимизации КЛ для базы данных Statlog NASA Shuttle
За основу для сравнения возьмем ситуацию линейного сдвига всех переменных в диапазон [-1,1] по формуле (1), КЛ выборки при этом равна 2332.
Выполним итеративное пошаговое уточнение нормировки - каждый раз дополнительно нелинейно предобрабатывается одна независимая переменная. Исходя из эмпирических соображений, для возможности "подтягивания" хвостов распределений в качестве масштабирующей нелинейной функции φ(x): R→ (-1,1) взята сигмоида
Получение нулевых средних для входных сигналов сети ускоряет градиентное обучение, поскольку снижает отношение максимального и минимального ненулевого собственных чисел матрицы вторых производных целевой функции по параметрам сети [3,4].
Иногда проводят и предварительную (перед линейным масштабированием) нелинейную предобработку - например, логарифмирование. При одновременном же рассмотрении всего набора независимых признаков можно убрать линейные корреляции между признаками, что также положительно влияет на скорость обучения [3,4].
Настоящая работа лежит в рамках специализированного подхода по построению предобработки путем привлечения информации и об отдельных "знаковых" примерах выборки. Примером подобной идеологии может служить работа [5], где для получения робастности к выбросам в независимых переменных кластеризуются данные обучающей выборки, и каждая статистически достоверно вылетающая за типичный радиус разброса для своего кластера точка (пример) проецируется по направлению к центру кластера.
Идея минимизации выборочной константы Липшица
На практике при предобработке данных обычно не оценивается получаемая в итоге "сложность" обучающей выборки для нейронной сети. В [1,2] предложено оценивать значение константы Липшица (далее КЛ) обучающей выборки. КЛ выборки
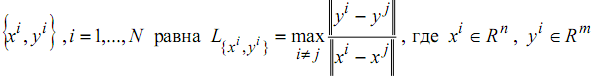- вектора
входных
сигналов и требуемых выходныx сигналов нейросети. Показано [6], что КЛ выборки влияет на процесс обучения и свойства обученной сети, и при предобработке выборки нужно минимизировать КЛ. Здесь результат [6] расширен в плане обсуждения и сравнения с иными стратегиями предобработки.
Поскольку КЛ выборки определяется примерами с разными ответными и близкими входными частями, то целенаправленно предобрабатывать нужно входные признаки, имеющие различные значения для этих конфликтных примеров.
Для снижения КЛ в [1,2] даны схемы предобработки количественного признака путем преобразования его в бόльшее число переменных. Однако, эти схемы не дают нулевые средние значения получаемых величин ñ каждую из последних может потребоваться дополнительно центрировать и масштабировать.
Расчет КЛ требует порядка (n+m)N2 операций, где N, n, m - число примеров выборки, входных и выходных сигналов сети соответственно. Современные ПК вычисляют КЛ выборок n+m ≈ 100/200 и N ≤ 50000 за минуты/десятки минут. Обучение нейросетей при этом требует бoльшего или сопоставимого времени.
При непересекающихся классах возможно обучение на малом предварительно отобранном наборе наиболее близких друг к другу примеров разных классов - примеров, между которыми и должна проходить разделяющая поверхность [7,8]. Эту идею можно применять и для уменьшения числа примеров, участвующих в расчете КЛ, так как при трансформации признака любым монотонным отображением R → R отобранные примеры по прежнему будут располагаться вдоль границы решения. Поэтому становится возможен быстрый неоднократный расчет КЛ на отобранном меньшем числе примеров с целью целенаправленного подбора уже самих способов предобработки из класса монотонных функций. Однако, задача прогноза либо иные методы active pattern selection (как метод [9] минимизации ошибки обобщения путем динамической селекции обучающих примеров) не позволяют предварительно отбирать малое число примеров.
Исходные данные для экспериментов и использованные алгоритмы
Взята известная база данных Statlog NASA Shuttle [10,11]: 43500 обучающих и 14500 тестовых примеров, 9 количественных входных признаков, классификация на 7 классов (при очень неравномерном распределении примеров по классам). Использовался авторский нейроимитатор NeuroPro, выбранные алгоритмы и стратегии были таковы:
• Взяты сети со скрытым слоем из 15 нейронов с сигмоидами f(x)=x/(0.1+|x|) и линейными выходными нейронами. Синапсы изначально равномерно распределены в [-0.1,0.1] и при обучении не ограничиваются. Для каждого способа предобработки выборки обучались копии 20-ти первоначально сгенерированных нейросетей.
• Для обучения брались все примеры обучающей выборки, на тестовой выборке выполнялось только тестирование обученных сетей. Использовался метод сопряженных градиентов в пакетном (batch) режиме с оптимизацией шага.
• Использовалась специальная классификаторная целевая функция из [1], веса классов установлены обратно пропорционально числу примеров в классе.
• Обучение прерывалось при распознавании правильно и с заданной надежностью 99% примеров обучающей выборки. Реально при этом правильно, но может быть с недостаточной надежностью, классифицировалось 99.7-99.9% примеров выборки.
• Обученные сети на тестовой выборке давали >99.6% правильных ответов. При обучении не использовались приемы увеличения обобщающей способности сетей.
Целенаправленная минимизации КЛ для базы данных Statlog NASA Shuttle
За основу для сравнения возьмем ситуацию линейного сдвига всех переменных в диапазон [-1,1] по формуле (1), КЛ выборки при этом равна 2332.
Выполним итеративное пошаговое уточнение нормировки - каждый раз дополнительно нелинейно предобрабатывается одна независимая переменная. Исходя из эмпирических соображений, для возможности "подтягивания" хвостов распределений в качестве масштабирующей нелинейной функции φ(x): R→ (-1,1) взята сигмоида
Значение
c
подбиралось так, чтобы
увеличить
расстояние по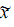 
между примерами, определяющими КЛ
выборки, а M изначально равнялось
выборочному
среднему M(x), но тоже могло уточняться. При подборе c, M дополнительно
визуально контролировался получаемый закон
распределения .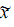
Последовательные 6 шагов нелинейной нормировки уменьшили КЛ до 254, 92.5, 80.7, 75.9, 57.6, 44.4 соответственно. Число шагов определялось не достигнутой КЛ, а достаточностью объема полученной в итоге информации для наблюдения и объяснения тенденций. Нелинейной предобработке были последовательно подвергнуты переменные 2, 8, 2 (была заново уточнено правило нормировки этой переменной), 7, 5, 9.
На Рис.1 даны гистограммы распределения значений исходных и пяти нелинейно предобработанных признаков. Видно, что часто используемые требования максимизации энтропии каждого отдельного признака или максимизации совместной энтропии признаков реально являются необязательными ñ КЛ выборки не всегда определена именно признаками с минимальной исходной энтропией.
Линейное масштабирование (2) исходных данных даст для предобработанных величин значительно бόльшие интервалы значений, чем обеспечиваемый (1) интервал [-1,1] - так, наибольший интервал ≈(-96,93) будет для признака 4. В данном случае и для целей экспериментирования большие интервалы изменения предобработанных величин приемлемы. КЛ выборки при этом снижается до значения 36.5.
между примерами, определяющими КЛ
выборки, а M изначально равнялось
выборочному
среднему M(x), но тоже могло уточняться. При подборе c, M дополнительно
визуально контролировался получаемый закон
распределения . Последовательные 6 шагов нелинейной нормировки уменьшили КЛ до 254, 92.5, 80.7, 75.9, 57.6, 44.4 соответственно. Число шагов определялось не достигнутой КЛ, а достаточностью объема полученной в итоге информации для наблюдения и объяснения тенденций. Нелинейной предобработке были последовательно подвергнуты переменные 2, 8, 2 (была заново уточнено правило нормировки этой переменной), 7, 5, 9.
На Рис.1 даны гистограммы распределения значений исходных и пяти нелинейно предобработанных признаков. Видно, что часто используемые требования максимизации энтропии каждого отдельного признака или максимизации совместной энтропии признаков реально являются необязательными ñ КЛ выборки не всегда определена именно признаками с минимальной исходной энтропией.
Линейное масштабирование (2) исходных данных даст для предобработанных величин значительно бόльшие интервалы значений, чем обеспечиваемый (1) интервал [-1,1] - так, наибольший интервал ≈(-96,93) будет для признака 4. В данном случае и для целей экспериментирования большие интервалы изменения предобработанных величин приемлемы. КЛ выборки при этом снижается до значения 36.5.
Свойства
обученных нейросетей для разных состояний обучающей выборки
На Рис.2 дан график КЛ для разных способов предобработки обучающей выборки - состояние 1 на Рис.2-Рис.4 соответствует отмасштабированной по формуле (1) выборке; состояния 2-7 соответствуют шести дополнительным шагам нелинейной нормировки (3) отдельных переменных; состояние 8 соответствует нормировке всех исходных данных по формуле (2). На Рис.3-4 точками даны значения свойств обученных сетей для разных состояний выборки, линиями даны графики средних значений. Для каждого состояния выборки обучались копии 20 исходных сетей-эталонов.
Видно (Рис.3), что снижение КЛ выборки приводит в итоге, по крайней мере для этой задачи, к снижению среднего требуемого числа итераций обучения на порядок. Под итерацией обучения здесь понимался однократный расчет градиента целевой функции по обучающей выборке и подбор оптимального шага вдоль надстроенного над градиентом направления спуска (требует нескольких просмотров обучающей выборки). Рис.4 показывает уменьшение с.к.о. распределений и, соответственно, модулей значений весов синапсов обученных сетей. Это может снизить конфликт между слагаемыми специальной регуляризующей целевой функции, например, функции [12]
-
где W -
набор
весов wi,
i=1, …, K
синапсов, Htrain(W)
Уменьшение весов синапсов по модулю также означает, что границы диапазона возможного изменения значений синапсов (если такие границы по каким-то причинам введены пользователем или навязаны программой-нейроимитатором) при обучении сети будут достигаться реже, и обеспеченная структурой (топологией) информационная емкость сети не будет дополнительно ограничена сверху лимитами на веса синапсов.
Видно, что даже разные линейные способы масштабирования каждого отдельного признака, т.е. формулы (1) и (2), могут давать в итоге отличающиеся на порядок итоговые результаты для свойств выборок и обученных по этим выборкам нейросетей.
Интегральные эффекты
Кроме способов предобработки, на КЛ выборки также может влиять и способ кодирования пропущенных значений: в случае неполных данных и наличия развитых способов оцифровки пропусков (использованная программа NeuroPro, нейропрограммы Trajan, Statistica Neural Networks) необходим контроль с этой стороны.
Монотонной зависимости эффектов от КЛ выборки может не быть, если при новой схеме предобработки спектр матрицы вторых производных целевой функции по весам синапсов существенно меняется в худшую с точки зрения градиентных алгоритмов обучения сторону [3,4]. Пример: для шага 2 возьмем для признака 2 формулу (2) вместо ранее взятой (3). При сохранении КЛ равной 254, среднее число итераций обучения не снижается, как ранее, с 854 до 385 (Рис.3), а растет до 1002 (Рис.5). Причина - рост отношения максимального и минимального ненулевого собственных чисел матрицы Гессе, т.е. рост овражности рельефа целевой функции в пространстве весов синапсов.
На Рис.2 дан график КЛ для разных способов предобработки обучающей выборки - состояние 1 на Рис.2-Рис.4 соответствует отмасштабированной по формуле (1) выборке; состояния 2-7 соответствуют шести дополнительным шагам нелинейной нормировки (3) отдельных переменных; состояние 8 соответствует нормировке всех исходных данных по формуле (2). На Рис.3-4 точками даны значения свойств обученных сетей для разных состояний выборки, линиями даны графики средних значений. Для каждого состояния выборки обучались копии 20 исходных сетей-эталонов.
Видно (Рис.3), что снижение КЛ выборки приводит в итоге, по крайней мере для этой задачи, к снижению среднего требуемого числа итераций обучения на порядок. Под итерацией обучения здесь понимался однократный расчет градиента целевой функции по обучающей выборке и подбор оптимального шага вдоль надстроенного над градиентом направления спуска (требует нескольких просмотров обучающей выборки). Рис.4 показывает уменьшение с.к.о. распределений и, соответственно, модулей значений весов синапсов обученных сетей. Это может снизить конфликт между слагаемыми специальной регуляризующей целевой функции, например, функции [12]
-
где W -
набор
весов wi,
i=1, …, K
синапсов, Htrain(W)Уменьшение весов синапсов по модулю также означает, что границы диапазона возможного изменения значений синапсов (если такие границы по каким-то причинам введены пользователем или навязаны программой-нейроимитатором) при обучении сети будут достигаться реже, и обеспеченная структурой (топологией) информационная емкость сети не будет дополнительно ограничена сверху лимитами на веса синапсов.
Видно, что даже разные линейные способы масштабирования каждого отдельного признака, т.е. формулы (1) и (2), могут давать в итоге отличающиеся на порядок итоговые результаты для свойств выборок и обученных по этим выборкам нейросетей.
Интегральные эффекты
Кроме способов предобработки, на КЛ выборки также может влиять и способ кодирования пропущенных значений: в случае неполных данных и наличия развитых способов оцифровки пропусков (использованная программа NeuroPro, нейропрограммы Trajan, Statistica Neural Networks) необходим контроль с этой стороны.
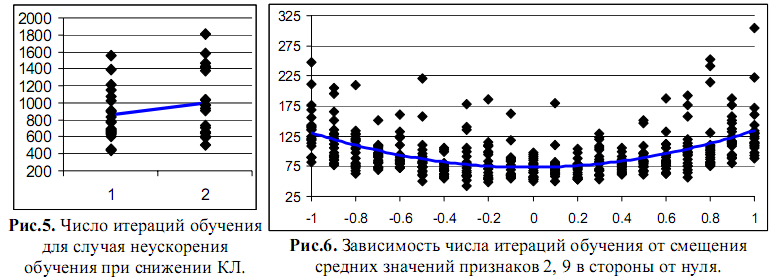
Монотонной зависимости эффектов от КЛ выборки может не быть, если при новой схеме предобработки спектр матрицы вторых производных целевой функции по весам синапсов существенно меняется в худшую с точки зрения градиентных алгоритмов обучения сторону [3,4]. Пример: для шага 2 возьмем для признака 2 формулу (2) вместо ранее взятой (3). При сохранении КЛ равной 254, среднее число итераций обучения не снижается, как ранее, с 854 до 385 (Рис.3), а растет до 1002 (Рис.5). Причина - рост отношения максимального и минимального ненулевого собственных чисел матрицы Гессе, т.е. рост овражности рельефа целевой функции в пространстве весов синапсов.
Итак,
минимизация
КЛ
выборки не является
самодостаточной и
открыт вопрос определения баланса
факторов,
влияющих на скорость обучения.
При предобработке
проще всего дополнительно
достигать
нулевых средних значений
переменных [3,4].
Ненулевые средние действительно
могут
замедлять обучение. Пусть переменные 2, 9
предобработаны через (2), а остальные -
через
(1), КЛ при этом равна 36.8. На Рис.6
показано число
итераций обучения 20 сетей при децентрировании входных сигналов 2 и 9,
линией дан квадратичный тренд, построенный над средними значениями
серий.
Имеется еще
один качественный
аспект -
шум в данных. Шум играет
ту же
ухудшающую роль, что и
разрывность аппроксимируемой функции: при
обучении
нейросеть постепенно вводит всё
более
высокочастотные члены разложения для
описания
скачка функции в области разрыва
или
для запоминания шума [13].
Это в
итоге ухудшает интерполяцию,
противодействием
является явная регуляризация решения
(например,
по Тихонову - нейровариант дан
в
[14]). Задачу классификации тоже
можно трактовать как
аппроксимацию
разрывной функции, поэтому здесь
применялся
другой возможный подход [13]:
с помощью
предобработки уменьшалась плотность точек выборки около
области
разрыва, что и выражалось в итоге в снижении КЛ.
Для разрывных
аппроксимируемых
функций
обычно можно локализовать область, точки которой
порождают
высокую КЛ, но шум может давать высокие КЛ и на всей
области значений переменных.
Поэтому для
первого случая можно получить бoльшее
относительное
снижение КЛ, чем для
второго, более гибко подобрав
предобработку.
Заключение
Полученные
результаты и выводы
являются
предварительными - необходимы дополнительные исследования для
подтверждения и уточнения тенденций, объяснений и гипотез, для изучения
устойчивости эффектов и степеней их проявления.
Однако,
наблюдение за
отдельными,
потенциально интересными показателями затрудняется
при
использовании многих эффективных приёмов и нейроалгоритмов. Так,
целевые функции с допуском
на
точность решения примера
позволят эффективно
оценивать [4] максимальное собственное
число
матрицы вторых производных целевой фунции по параметрам сети
только для начальных итераций обучения, так как затем всё большее число
примеров будет укладываться в допуск по точности, и всё меньшее число
недостаточно точно решенных примеров можно будет использовать для
оценивания.
Но всё же изучение
эффективности различных принципов предобработки
данных и их влияния на
свойства
результирующих нейросетей является
востребованным и
необходимым для возможности
расширения и
уточнения набора формальных правил
организации
процесса предобработки для задач обучения с учителем.
Литература
1. Миркес Е.М. Нейрокомпьютер: проект стандарта. Новосибирск: Наука, 1999. - 337с.
1. Миркес Е.М. Нейрокомпьютер: проект стандарта. Новосибирск: Наука, 1999. - 337с.
2. Горбань
А.Н., Россиев
Д.А.
Нейронные сети на персональном
компьютере. Новосибирск: Наука, 1996. - 276с.
3. LeCun Y., Kanter I., Solla S.A. Second order properties of error surfaces: learning time and generalization / Advances in Neural Information Processing Systems 3 (1990). Morgan-Kaufmann, 1991. pp.918-924.
4. LeCun Y., Bottou L., Orr G.B., M¸ller K.-R. Efficient BackProp / Neural Networks: Tricks of the trade (G.Orr and K.M¸ller, eds.), Springer Lecture Notes in Comp. Sci. 1524, 1998. pp.5-50.
5. Hamalainen J.J., Jarvimaki I. Input projection method for safe use of neural networks based on process data / Proc. IJCNN'1998, Anchorage, Alaska, USA, 1998. ñ pp.193-198.
6. Царегородцев В.Г. Предобработка обучающей выборки, выборочная константа Липшица и свойства обученных нейронных сетей // Материалы Х Всеросс. семинара "Нейроинформатика и ее приложения", Красноярск, 2002. 185с. - С.146-150.
7. Hara K., Nakayama K. Selection of minimum training data for generalization and on-line training by multilayer neural networks / Proc. IEEE ICNN'1996, Washington, DC, USA, 1996, Vol.1. - pp.436-441.
8. Hara K., Nakayama K., Kharaf A.A.M. A training data selection in online-training for multilayer neural networks / Proc. IEEE IJCNN'1998, Anchorage, Alaska, USA, 1998. ñ pp.2247-2252.
9. Robel A. Dynamic pattern selection for faster learning and controlled generalization of neural networks / Proc. ESANN'1994, Brussels, Belgium. 1994. - pp.187-192.
10. Michie D., Spiegelhalter D.J., Taylor C.C. Machine learning, neural and statistical classification. Elis Horwood, London, 1994.
11. UCI KDD Database Repository. http://kdd.ics.uci.edu/
12. Ishikawa M., Yoshida K., Amari S. Designing regularizers by minimizing generalization error /Proc. IEEE IJCNN'1998, Anchorage, Alaska, USA, 1998.- pp.2328-2333.
13. Chauvin Y. Dynamic behavior of constrained back-propagation networks / Advances in Neural Information Processing Systems 2 (1989). Morgan-Kaufmann, 1990.ñ pp.642-649.
14. Drucker H., LeCun Y. Improving generalization performance using double backpropagation / IEEE Trans. on Neural Networks, 1992, Vol.3, №6. - pp.991-997.
3. LeCun Y., Kanter I., Solla S.A. Second order properties of error surfaces: learning time and generalization / Advances in Neural Information Processing Systems 3 (1990). Morgan-Kaufmann, 1991. pp.918-924.
4. LeCun Y., Bottou L., Orr G.B., M¸ller K.-R. Efficient BackProp / Neural Networks: Tricks of the trade (G.Orr and K.M¸ller, eds.), Springer Lecture Notes in Comp. Sci. 1524, 1998. pp.5-50.
5. Hamalainen J.J., Jarvimaki I. Input projection method for safe use of neural networks based on process data / Proc. IJCNN'1998, Anchorage, Alaska, USA, 1998. ñ pp.193-198.
6. Царегородцев В.Г. Предобработка обучающей выборки, выборочная константа Липшица и свойства обученных нейронных сетей // Материалы Х Всеросс. семинара "Нейроинформатика и ее приложения", Красноярск, 2002. 185с. - С.146-150.
7. Hara K., Nakayama K. Selection of minimum training data for generalization and on-line training by multilayer neural networks / Proc. IEEE ICNN'1996, Washington, DC, USA, 1996, Vol.1. - pp.436-441.
8. Hara K., Nakayama K., Kharaf A.A.M. A training data selection in online-training for multilayer neural networks / Proc. IEEE IJCNN'1998, Anchorage, Alaska, USA, 1998. ñ pp.2247-2252.
9. Robel A. Dynamic pattern selection for faster learning and controlled generalization of neural networks / Proc. ESANN'1994, Brussels, Belgium. 1994. - pp.187-192.
10. Michie D., Spiegelhalter D.J., Taylor C.C. Machine learning, neural and statistical classification. Elis Horwood, London, 1994.
11. UCI KDD Database Repository. http://kdd.ics.uci.edu/
12. Ishikawa M., Yoshida K., Amari S. Designing regularizers by minimizing generalization error /Proc. IEEE IJCNN'1998, Anchorage, Alaska, USA, 1998.- pp.2328-2333.
13. Chauvin Y. Dynamic behavior of constrained back-propagation networks / Advances in Neural Information Processing Systems 2 (1989). Morgan-Kaufmann, 1990.ñ pp.642-649.
14. Drucker H., LeCun Y. Improving generalization performance using double backpropagation / IEEE Trans. on Neural Networks, 1992, Vol.3, №6. - pp.991-997.