Бакланов А.В. - ОБГРУНТУВАННЯ РЕЖИМУ ГАЛЬМУВАННЯ КОНВЕЄРА

Аннотация

Бакланов А.В. Обгрунтування режиму пуску стрічкового конвеєру. Розглянута математична модель розрахунку динамічних процесів в стрічковому конвеєрі при пуску.

Общая постановка проблемы

Математична модель розрахунку динамічних процесів в стрічковому конвеєрі

Моделювання процесів пуску стрічкових конвеєрів зводиться до заміни неперервної моделі на дискретну, в якій зв'язки між точковими масами замінюються пружними і дисипативних зв'язками. В результаті, модель описується системою звичайних диференціальних рівнянь з відповідними початковими і граничними умовами. Рішення отриманої системи - в загальному випадку нелінійних звичайних диференціальних рівнянь - представляє також великі труднощі. Тому в задачах оптимального керування пуском стрічкового конвеєра така модель не має практичного застосування. Для вирішення завдань пуску застосовувався метод перетворення Лапласа. В результаті, знайдені рішення задач пуску стрічкового конвеєра для лінійних характеристик двигуна. Однак, в загальному випадку для нелінійних і розривних характеристик двигуна цей метод не застосовний. Отже, в даний час не існує адекватної математичної моделі динамічних процесів пуску стрічкових конвеєрів з нелінійними і розривними характеристиками двигунів. Для модулювання процесів пуску стрічкового конвеєру користується метод припасовки (зшивки). Сутність метода припасовки складається в тому, що диференційне рівняння, які описують динамічний процес, вирішується у загальному вигладі для кожної окремої лінійної ділянки апроксимувальної характеристики двигуна. Потім, по заданим початковим і граничним умовам, які є рішенням диференціального рівняння процесу для попередньої лінійної дільниці апроксимувальної характеристики двигуна, знаходяться довільні константи рішення диференціального рівняння процесу для подальшої лінійної ділянки характеристики двигуна. Так послідовно знаходяться рішення для всіх лінійних ділянок апроксимувальної характеристики двигуна.

Рис.1 - Стрічковий конвеєр

Система диференціальних рівнянь, описуючі динамічні процеси пуску стрічкового конвеєру, має вигляд:

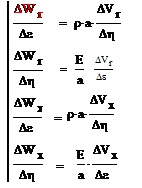
При початкових умовах n=0:

Vг(E,0)=Vx(E,0)=0; Wг(E,0)=Wx(E,0)=0

де Wг(E,n), Wx(E,n) – динамічні складові натягнень на вантажної і холостої гілках стрічки конвеєра відповідно, Н; Vг(?,?), Vx(?,?) - швидкості точок вантажної і холостої гілках стрічки конвеєра відповідно, м/с; ?, ? - відповідно безрозмірні координати і час; а - швидкість поширення пружних збурень в стрічці, м/с; Е - агрегатна жорсткість стрічки при її розтягуванні, Н; ? - еквівалентна погонна щільність стрічки, кг/м ( ? = Е/ а^2).

Безрозмірні координати і безрозмірний час визначається по формулам:

E= х/L; n=at/L

де х – координата, спрямована уздовж стрічки в напрямку головного барабана, с центром на осі хвостового барабану конвеєру, м; t - поточний час, с; L – довжина контуру стрічки конвеєру, м.

Граничні умови на хвостовому і приводному барабанах залежать від типу натяжного пристрою.

Для жорсткого натяжного пристрою в силу умови нерозривності стрічки маємо:

на хвостовому барабані: при E=о

Vг(0,n)= -Vx(0,n), Wг(0,n)= -Wx(0,n);

на приводному барабані при: E=1/2

Vг(1/2,?)= -Vx(1/2,n)

Wг(1/2,?) -Wx(1/2,n)= F(Vг) – G1 - (a*m/L)*dV/dn

де F(Vг) – пускова характеристика приводу в координатах F, V, Н; G1 - сила опору руху стрічки і вантажу, яка включає скочующуся силу від ваги вантажу і стрічки конвеєра, Н; m – приведена маса вантажу обертових частин приводу стрічкового конвеєру, кг.

При цьому пускова характеристика двигуна апроксиміровалась кусочно-лінійним сплайном, котрий можна подати у вигляді

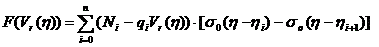
де Ni - координата перетину i-ї лінійної ділянки апроксимовуваноъ характеристики з віссю OF, H; q - тангенс кута нахилу лінійної ділянки апроксимувавоної характеристики до осі, кг/с; n - моменти переходу з одного лінійного ділянки пускової характеристики на інший; 6(n) - одинична функція Хевисайда; n – кількість лінійних ділянок характеристики.

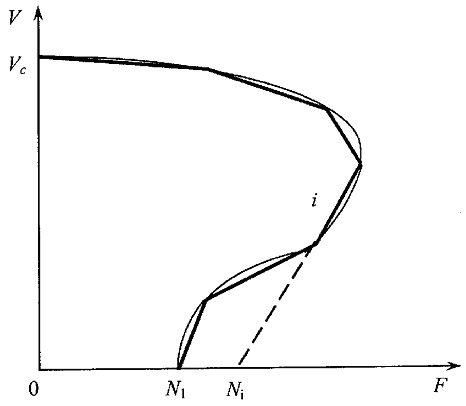
Рис.2 - Пускова характеристика приводу

Згідно методу припасування, отримаємо рішення системи диференціальних рівнянь для i-ї лінійної ділянки апроксимовуваної характеристики двигуна.

Отже, обчисливши швидкість стрічки на приводному барабані, підставляючи ці значення, отримаємо швидкість і динамічне зусилля в будь-якій точці стрічки конвеєра.

Выводы

Пуск конвеєрів через великі інерційних мас і статичних навантажень відрізняється значною тривалістю і супроводжується істотним нагріванням двигунів. Перевантаження конвеєра, знижена напруга живлення, деякі види несправності в механічному та електричному обладнанні можуть призводити до додаткового затягування процесу пуску і внаслідок цього до неприпустимого перевищення температури двигуна. Крім того, перевантаження стрічкових конвеєрів може призвести до пробуксовування тягового елемента на приводному органі При цьому закінчився процес пуску двигуна не виводить конвеєр на робочу швидкість, а тривале буксування призводить до псування тягового елемента, тому у всіх випадках тривалого пуску конвеєра понад регламентованого часу привід необхідно відключити.

Список использованной литературы

1.Бужинский И.А. Определение рациональных пусковых характеристик привода наклонного ленточного конвейера / И.А. Бужинский, Р.А. Кирия// Машины для предприятий горной промышленности. – К., 1986. - с.30-38
2. Кирия Р.В. Влияние типа натяжного устройства и места его установки на динамику пуска ленточного конвейера / Р.В. Кирия, В.Ю. Масютенко, И.А. Бужинский// Сб. науч. тр. Геотехническая механика – Д. -2006. – Выш. №67. – с.73-83.
3. Попов Е.П. Теория нелинейных систем автоматического регулирования и управления. – М., 1988. – 256с.
4. Галкин В. И. , Дмитриев В. Г. , Дьяченко В. П. , Запенин И. В. , Шешко Е. Е.Современная теория ленточных конвейеров горных предприятий. Учебное пособие; М.: Горная книга, 2011. - 544 с.