Аннотация
Bahman Bahmani Firouzi, Ehsan Jamshidpour, Taher Niknam. Новый метод определения параметров крупных синхронных генераторов с помощью генетического алгоритма B этой статье представлена и cмоделирована возможность определения параметров синхронного генератора посредством линейных испытаний в оперативном режиме
Реферат: в этой статье представлена и cмоделирована возможность определения параметров синхронного генератора посредством линейных испытаний в оперативном режиме с использованием генетического алгоритма на синхронном генераторе мощностью 400 МВА на электростанции «BISOTUN» в Иране. Данные оперативного временного промежутка получены имитацией возмущения генератора. Динамические параметры продольной и поперечной осей найдены обработкой переходной характеристики синхронной машины во вращающемся состоянии. Генетический алгоритм использован для идентификации требуемых параметров. Проведение этого опыта требует большей мощности и времени тестирования, но обеспечивает большую точность благодаря большому потокосцеплению и условиям вращения. Ключевые слова: синхронный генератор, определение параметров, оперативные испытания, генетический алгоритм.
Введение
Моделирование генераторов играет важную роль в планировании работы и послеаварийном анализе системы. Определение параметров синхронного генератора может быть выполнено двумя основными методами: статическим и характеристики вращения во временной области. Статический опыт с частотной областью во времени получил быстрое распространение благодаря простоте его использования даже на очень больших машинах. Он все еще иногда критикуется за чрезмерно низкий уровень испытательных токов, стоит ли говорить, что эффект вращения двойных осей, влияние центробежных сил на демпферные обмотки и влияние магнитного рассеивания не учитываются при использовании статического метода. [1,2] Эти ограничения инициировали появление метода характеристики вращения во временной области, базирующемся на небольших или значительных сигналах о возмущениях вокруг области номинальных рабочих параметров. Использование генетического метода для определения параметров является новым подходом и в этой статье используется для определения параметров синхронной машины по данным характеристик во временной области. Целью работы является демонстрация нового подхода, основанного на идентификации параметров синхронной машины генетическим алгоритмом из опыта характеристик во временной области по оперативным параметрам с малыми возмущениями, полученным резким изменением опорного напряжения или момента. С этой целью вводятся малые и большие возмущения и маленькие возмущения отображаются как подходящие для определения динамических параметров синхронного генератора на ТЭС «BISOTUN». Эта статья состоит из следующих частей: В разделе (II) даются характеристики и применяемая модель синхронного генератора электростанции «BISOTUN». Раздел (III) описывает метод характеристики вращения во временной области, маленькие и большие возмущения и вводит полный алгоритм оперативного метода, раздел (IV) описывает основные положения применяемого генетического алгоритма. В разделе (V) показаны результаты имитации маленьких возмущений для генератора электростанции «BISOTUN». Полный алгоритм оперативного метода имитируется в разделе (VI) и показываются найденные и сымитированные конечные результаты для сравнения.
Характеристики синхронного генератора и его модель
Синхронные генераторы ТЭС «BISOTUN» являются неявнополюсными турбогенераторами, изготовленными компанией «ANSALDO». Характеристики объекта изучения следующие: Статор: 400 МВА, 320 МВт, 11547 А, 50 Гц, 3000 об/мин, cos?=0.85/ Система возбуждения статическая щеточная. Из-за неявнополюсной формы ротора и его высокой скорости вращения для этого генератора рассматривается модель (2-2) [5]. Эквивалентная схема модели показана на рис. 1.
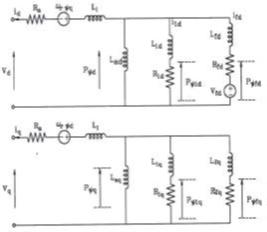Рис. 1 – Эквивалентная схема модели
Метод характеристики вращения во временной области
Метод характеристики вращения во временной области - это метод для определения параметров синхронной машины из возмущений вблизи рабочей области машины [1,2]. Традиционный оперативный опыт для моделирования машины включает в себя характеристики больших возмущений, таких как синхронизация, сброс нагрузки и опыт коммутации. Благодаря большим переходным отклонениям, появляющимся в результате этих опытов, количество и тип опытов может быть ограничено проблемой устойчивости системы и мощностью рассматриваемого оборудования [3, 4, R.L.6]. с другой стороны регистрация действительных линейных рабочих данных малыми возмущениями не оказывает значительного влияния на общее рабочее состояние генерирующей системы. Следовательно, желательно сконструировать и отрегулировать параметры модели синхронной машины на базе характеристик малых возмущений. В этом исследовании данные сортированы по характеристикам малых возмущений. Динамика отображается изменением на 1% и 2% в системе возбуждения и входном моменте. Такой опыт может быть произведен в нормальных рабочих условиях без каких-либо серьезных влияний на всё состояние системы. С учетом вышеизложенных пояснений метод характеристики вращения во временной области состоит из трех основных шагов. Для этого метода некоторые сигналы должны быть получены из изучаемой машины или для имитируемой по возмущениям машины. Эти сигналы: Va(t), Vb(t), Vc(t), ia(t),ib(t),ic(t), ??(t), ?r(t), ??(t) угол вылета ротора и ?r(t) скорость ротора. Отношение этих двух сигналов описывается уравнением (1) [5].
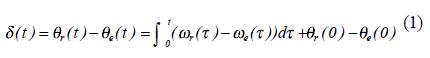
Блок схема метода характеристики вращения во временной области показана на рис. 2.
Рис. 2 – Блок-схема метода вращения характеристики во временной области
Измерением значений на рис. 2 могут быть получены значения токов и напряжений на клеммах по продольной и поперечным осям Vd, Vq,, id и iq. После подключения машины к энергосистеме со сбалансированными параметрами, круговая частота ?, изменяется незначительно от номинальной частоты. Следовательно, вместо использования обычных уравнений Парка-Горева, могут быть использованы следующие уравнения [3,6].
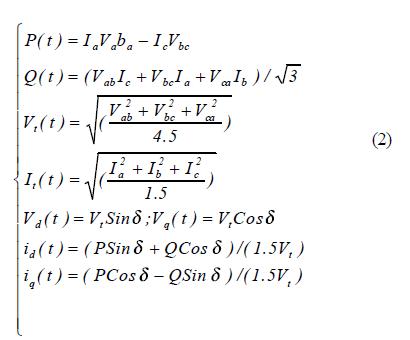
Как видно из рис. 2 первая главная часть алгоритма характеристики вращения во временной области - расчет wd и wq интегрированием измеренных (или имитированных) данных. После подключения машины через трансформатор к энергосистеме производные потокосцеплений продольной и поперечной осей не учитываются. Это допущение верно с момента, когда уровень изменения выходных напряжения и тока машины пренебрежительно мал по сравнению с малыми возмущениями. Следовательно, ?d и ?q могут быть рассчитаны из следующих уравнений (3).
Вторая часть этого алгоритма – расчет ?d и ?q из модели синхронной машины. Для этой части используется модель машины Парка как пояснялось в разделе 2. Также для этой части используются id и iq как входные сигналы. Записав уравнения синхронной машины, можно рассчитать ?d и ?q по следующим уравнениям (4).
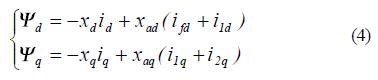
С этой целью, должны быть определены токи ротора. Таким образом, токи ротора записываются относительно потоков ротора и токов статора. Эти уравнения записаны в приложении А; следовательно потоки ротора могут рассчитаться решением следующих уравнений (5).
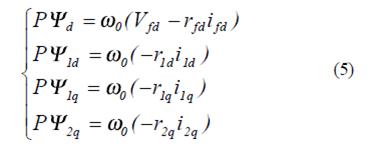
Уравнение выше в именованных единицах, а Р означает d/dt. wd и wq могут быть рассчитаны этим методом. Для данных расчетов должны быть определены параметры схемы замещения. Эти параметры получают в третьей основной части алгоритма. Эти параметры будут скорректированы согласно разницы между ?d и ?q на шагах 1 и 2. В этой статье эти результаты дает использование генетического алгоритма.
Генетический алгоритм как метод идентификации
Для определения динамических параметров синхронной машины использован генетический алгоритм. Это алгоритм начинается как любой другой оптимизационный алгоритм с определением оптимизационных параметров из функции затрат и стоимости. Он заканчивается подобно другим оптимизационным алгоритмам после проверки сходимости. Путь по элементам генетического алгоритма показан в виде блок-схемы на рис. 3 [7]. Для этого исследования в качестве оптимизационных параметров были взяты X , X , X??, X??, T??, T??, T???, T??. Суммарная квадратичная ошибка и относительная квадратичная ошибка, которые находились по уравнениям (6), рассматривались как стоимости.
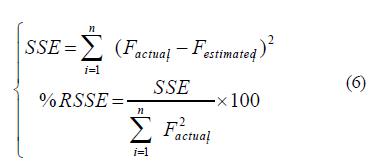
Где F – поток по продольной и поперечной осям. Factual - сигнал, который рассчитан на первой итерации метода характеристик вращения во временной области, а Festimated – выходной сигнал со второй итерации метода характеристик вращения во временной области и они рассчитаны из предполагаемых параметров.
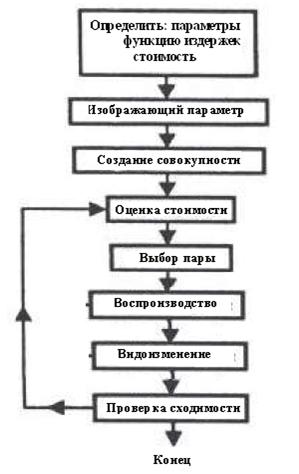Рис. 3 – Блок-схема продолжительного генетического алгоритма
Генетический алгоритм начинается определением исходной совокупности Nipop хромосом. Матрица отражает совокупность, в каждой строке в матрице массив (хромосом) Nparameterd,q постоянных значений параметров. Дается начальная совокупность Nipop хромосом, полная матрица из Nipopi Nparameterd,q произвольных значений генерируется следующим уравнением (7).
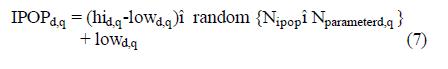
Где: произвольное {Nipop, Nparameterd,q } – функция, которая создает матрицу Nipop и Nparameterd,q унифицированных произвольных чисел между нулем и единицей. hi: наибольшее число в диапазоне параметров. low: наименьшее число в диапазоне параметров. Это общество хромосом недемократично. Ценность каждой ограничена функцией стоимости. Затем сортировкой исходной совокупности согласно минимальной стоимости выбирается для дальнейшего скрещивания Ngood хромосом, которые имеют наименьшую стоимость, а другие отбрасываются. При условии скрещивания, мутация и другие операторы генетической процедуры используются для получения совокупности из предыдущего шага. Применяя эту процедуру к совокупности итерационно, улучшаем функция стоимости; таким образом возможность мутаций уменьшается экспоненциально после каждой итерации. В этом исследовании начальная совокупность состоит из 100 хромосом, которые выбраны из 1000. Возможность скрещивания изменяется на протяжении работы программы. Остальные детали не описываются ради краткости. Добиваются условий сходимости SSE меньше, чем 0,0001, т. е. RSSE?0.001, которое было осуществлено в оптимизационной программе.
Моделирование оперативного метода для генератора
Форма входного сигнала, который применяется для определения параметров системы, должна давать различные режимы системы (постоянно для условий возбуждения). Белый шум или мнимая произвольная двоичная последовательность идеальна для идентификации, но генерация таких сигналов требует специального оборудования. Тем временем операторы обычно не позволяют применять эти сигналы в качестве входных. Известно, что изменение шага – самый легкий путь для получения динамических режимов любой системы. Эти изменения могут быть выполнены системой возбуждения (применяя внешний сигнал к узлу напряжения путем единичного изменения отпаек трансформатора или команды увеличения и уменьшения), системой управления (увеличение или уменьшение требуемой нагрузки) или сбросом нагрузки. Метод проведения опыта, который безопасен в проведении и не требует дорого оборудования это изменение шага напряжения или сброс нагрузки. Этот метод бы имитирован изменением на 1 % и 2 % напряжения возбуждения и входного момента, которые рассматриваю8тся как входное возмущение. Для имитации выводов машины, сначала моделируется синхронная машина, которая присоединена к шине бесконечной мощности через реактивное сопротивление. Эта модель выполнена в SIMULINK. С этого момента уровнем изменения выходного напряжения и тока машины пренебрегают в силу малых возмущений, производные потокосцеплений по продольной и поперечной осям не учитываются; таким образом, модель сети не содержит электрических соединений и для нее может быть принята векторная конфигурация. Вышеприведенные возмущения могут быть смоделированы в форме изменения шага с рабочих условиях. Эти возмущения выполняются для машины в установившемся рабочем режиме. Рисунки 4 и 5 показывают изменения выходных параметров машины под действием указанных возмущений, которые вводятся в машину в установившемся режиме за время 300 секунд.
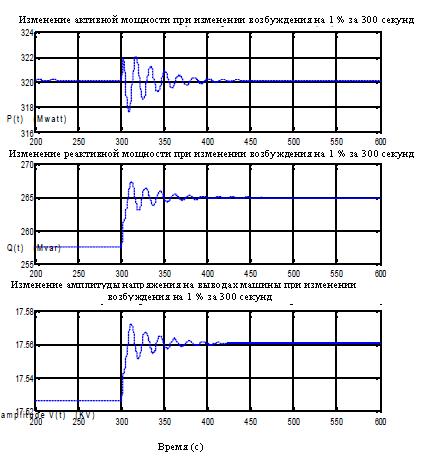Рис. 4 – Изменение выходных параметров машины при изменении возбуждения на 1 % за время 300 секунд
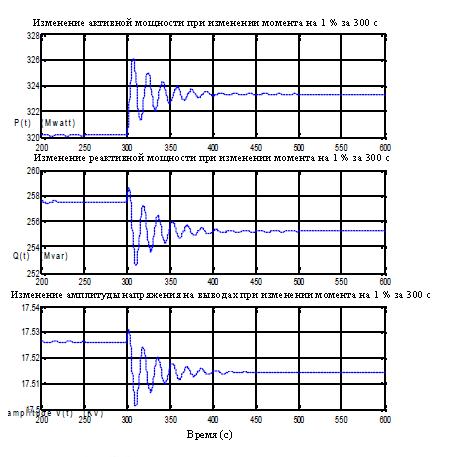Рис. 5 - Изменение выходных параметров машины при изменении входного момента вращения на 1 % за время 300 секунд
Моделирование алгоритма характеристики вращения во временной области и его результат
Полный алгоритм, объясненный выше, был смоделирован в MATLAB. Для идентификации параметров машины требуется использование генетического алгоритма [7] для измеренных входных-выходных сигналов. Эти сигналы были получены путем моделирования в разделе V посредством применения различных малых возмущений. Рисунок 6 показывает смоделированные и ожидаемые выходные параметры (потоки) на продольной и поперечной осях при различных малых возмущениях. Таблица 1 показывает смоделированные и предполагаемые параметры при различных возмущениях.
Рис. 6 – Моделируемый и предполагаемый потоки при изменении возбуждения на 1 % за 300 секунд
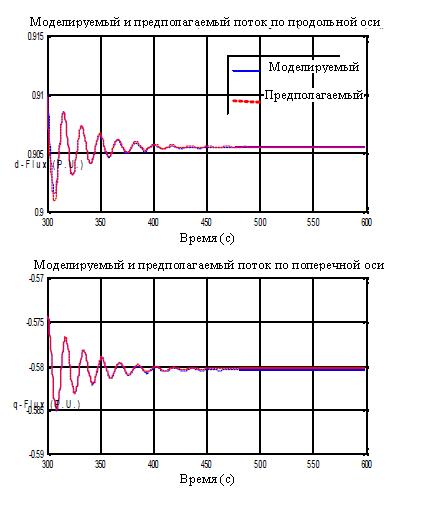Рис. 7 – Моделируемый и предполагаемый потоки при изменении момента на валу на 1 % за 300 секунд
Проверка достоверности модели
Проверка достоверности модели самый важный шаг в любом опыте определения параметров. Простейший путь проверки достоверности – сравнение ожидаемых результатов модели с полученными в результате имитации. Эта стратегия была выбрана для сравнения выходных параметров оценочной модели и имитационной (рабочей). Как показывают рисунки, все оценочные модели достаточно хороши. Другой критерий проверки ограничений полученных параметров – использование уравнения (8), которое применяется для изучения обоих осей.
Все оцененные параметры удовлетворяют вышеуказанным ограничениям. При этом таблица 2 показывает параметры, найденные в документах электростанции. Сравнение этих значений с соответствующими найденными значениями показывает точность модели.
Вывод
В этой статье представлена методика выполнения опыта для определения параметров машины для ТЭС «BISOTUN». Применяя малые возмущения для систем возбуждения и управления, удовлетворительно определены параметры модели. Генетический алгоритм использован для оценки параметров. Выведенная модель была проверена и ее реакции на одинаковые возмущения были очень близки к соответствующим выходным параметрам действующей машины. В конце концов было предложено изменение шага для системы возбуждения (изменением отпайки трансформатора), из-за его простоты и безопасности выполнения.
Использованная литература
1. Kamwa, I., P. Viarouge and E.J. Dickinson, 1991.
Identification of generalized models of
synchronous machines from time domain tests. IEE
Proceeding-C.
2. Wamkeue, R., I. Kamwa, X. Dai-Do and A.
Keyhani, 1999. Iteratively Reweighted Least
Square for Maximum Likelihood Identification of
Synchronous Machine Parameters from On-Line
Tests. IEEE Transactions on Energy Conversion,
14 (2).
3. Tsai, H., A. Keyhani, J. Demcko and R.G. Farmer,
1995. On-Line Synchronous Machine Parameter
Estimation From Small Disturbance Operating
Data. IEEE Transaction on Energy Conversion,
Vol: 10 (1).
4. Rusche, P.A.E., G.J. Brock, L.N. Hannet and J.R.
Willis, 1990. Test and Simulation of Network
Dynamic Response Using SSFR and RTDR
Derived Synchronous Machine Models. IEEE
Transactions on Energy Conversion, Vol: 5 (1).
5. Paul C. Krause, 1986. Analysis of Electric
Machinery. Mc Graw-Hill series in Electrical
Engineering, Power and Energy.
6. Horning, S., A. Keyhani and I, Kamwa, 1997. Online
Evaluation of a Round Rotor Synchronous
Machine Parameter Set Estimated From Standstill
Time-Domain Data. IEEE Transactions on Energy
Conversion, 12 (4).
7. Haupt, R.L. and S.E. Haupt, 1999. Practical
Genetic Algorithms. Jhon Wiely and Sons Inc.
8. Huang, C.T., Y.T. Chen, C.L. Chang, C.Y. Huang,
H.D. Chiang and J.C. Wang, 1994. On-Line
Measurement-Based Model Parameter Estimation
for Synchronous Generators; Model Development
and Identification Schemes. IEEE Transactions on
Energy Conversion, Vol: 9 (2).
9. Shande, S., Z. Shouzhen and H. Bo, 1991.
Identification of Parameters of Synchronous
Machine and Excitation System by On-Line Test.
IEE International Conference on Advances in
Power System Control, Operation and
Management, November 1991, HongK