Автор: Н.М. Погрібняк, В.В. Мухін, К.А. Удовіченко, О.О. Булгаков
Источник: Наукові праці Донецького національного технічного університету. Серія: “Електротехніка і енергетика”. - Донецьк: ДВНЗ «ДонНТУ», 2012.- №1(12) -2(13). – С. 192-196.
Більш, ніж 40 % з’єднань у промисловості виконується методом контактної зварки. Машини контактної зварки (МКЗ) працюють з низьким коефіцієнтом ввімкнення, а під час зварювання створюють суттєве навантаження [1]. Мережа живлення машин контактної зварки має бути перевірена за величиною втрати напруги, оскільки при зниженні напруги може виникнути брак зварного з’єднання. Для вибору захисту також необхідно розраховувати пікові струми, що виникають при роботі групи МКЗ.
У діючих Керівних вказівках з визначення пікових струмів і втрати напруги [2] застосовуються спрощення. По-перше, для визначення максимальних розрахункових значень пікових струмів і втрати напруги необхідно знати їх функції розподілу, які неможливо отримати через великий обсяг обчислень. Тому прийняття статистичного коефіцієнта за кривою, наведеною у діючих Керівних вказівках, при визначенні максимальних розрахункових значень пікових струмів і втрати напруги не є обґрунтованим. Значення статистичного коефіцієнта при розрахунку пікового струму і втрати напруги у діючих Керівних вказівках рекомендується приймати по єдиній кривій, однак функції розподілу пікових струмів і втрат напруги для однієї групи МКЗ можуть відрізнятися, оскільки на величину втрати напруги, а значить і на функцію її розподілу, на відміну від пікового струму, впливають ще й відстані від джерела живлення до місць підключення МКЗ. Отже, застосування єдиної кривої для визначення статистичного коефіцієнта є сумнівним. По-друге, втрати лінійних напруг, створювані двохфазними МКЗ, визначається із застосуванням усереднених коефіцієнтів, через що правильний результат для двохфазних машин може бути отриманий тільки при великій їх кількості і рівномірному розподілу між фазами та за відстанню від джерела живлення. Такий самий підхід щодо визначення втрат напруги, створюваних двохфазними машинами, використовувався і в попередній редакції Керівних вказівок [3]. Додаткова погрішність попередньої методики пов’язана із застосуванням двохступеневих впорядкованих діаграм пікових струмів і втрат напруги замість їх фактичних функцій розподілу.
Оскільки результат визначення втрати напруги суттєво впливає на остаточний вибір потужності трансформатора цехової трансформаторної підстанції та перетин шинопровода, що визначає капітальні витрати на електричну мережу, задача підвищення точності розрахунку є актуальною. Метою роботи є зменшення капітальних витрат на мережу живлення групи машин контактної зварки шляхом підвищення точності розрахунку втрат напруги і пікових струмів у ній.
Рішенням є максимальні розрахункові значення пікових струмів і втрат напруги, які визначаються за їх функціями розподілу. Для цього мають бути вирішені такі задачі:
1. Точного розрахунку струмів і напруг усіх ділянок електричної мережі живлення МКЗ при будь-якій комбінації ввімкнених зварювальних машин;
2. Розробки методики розрахунку функцій розподілу пікових струмів і втрат напруги для визначення максимальних розрахункових значень цих величин.
Для вирішення першої задачі розроблений алгоритм і відповідна програма [4]. Точність, з якою за нею визначаються струми і напруги усіх гілок, на перший погляд, для практичних розрахунків є надмірною, але це необхідно для використання її в якості складової алгоритму визначення функцій розподілу пікових струмів та втрати напруги, що використовуються для обґрунтування інженерних методів та оцінки їх точності.
При невеликій кількості МКЗ, маючи програму визначення струмів і напруг при довільній комбінації ввімкнених зварювальних машин, можуть бути розраховані точні функції розподілу пікових струмів і втрат напруги. Кількість сходинок функції розподілу для п зварювальних машин дорівнює
де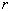 
– кількість ввімкнених МКЗ, 
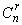– кількість сполучень з п по .
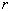Наприклад, для групи з 20 машин кількість сходинок буде більша за мільйон. Отже, навіть для такої невеликої групи зварювальних машин, розрахунок точних функцій розподілу потребуватиме значних витрат часу. Оскільки група може налічувати значно більшу кількість МКЗ, необхідне зменшення обсягу розрахунків. Це пропонується здійснити двома способами.
По-перше, оскільки необхідно визначити максимальні розрахункові значення пікових струмів і втрат напруги з граничною ймовірністю 
(приймається = 0,001, як і в [2, 3]), для рішення задачі достатньо з запасом 
розрахувати ділянки функцій розподілу до досягнення ними значення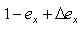 
.
Другим способом зменшення об’єму розрахунків є розподіл зварювальних машин на групи і перехід від розгляду можливих варіантів їх одночасного ввімкнення до перебору всіх варіантів ввімкнення різної кількості МКЗ з груп. Слід зазначити, що цей спосіб може бути застосований і у інших подібних випадках, наприклад, при оцінці електромагнітної сумісності, при изначенні розрахункових навантажень, тощо. При цьому розподіл електроприймачів по групам слід виконувати за їх впливом на параметр, що визначається, об’єднуючи у одну групу електроприймачі, що впливають однаково або подібно. Стосовно МКЗ, їх розподіл виконується на 7 груп в залежності від кількості фаз та того, до яких фаз підключені: 1 - 3 групи - однофазні, підключені до фаз АВ, ВС та СА відповідно; 4 – 6 – двохфазні, підключені до фаз АВ, ВС – 4 група; до фаз ВС, СА – 5 група; до фаз СА, АВ – 6 група; трифазні відносяться до 7 групи.
Необхідні ділянки функцій розподілу пікових струмів і втрат напруги розраховуються за середнім значенням коефіцієнта ввімкнення 
зварювальних машин, починаючи зі сходинки з ймовірністю 
, що відповідає вимкненому стану усіх машин. Далі кількість ввімкнених МКЗ зростає по одній і для кожного значення загальної кількості ввімкнених зварювальних машин розглядаються всі можливі варіанти ввімкнення різної кількості машин з груп з врахуванням їх кількостей у групах. Для кожного з варіантів розраховуються пікові струми, втрати напруг та його ймовірність
где i – порядковый номер группы; k – количество групп; mi – количество машин, отнесенных к i-ой группе; qi – количество включенных машин в i-ой группе.
Оскільки у групи можуть входити МКЗ різної потужності, виконується розрахунок "граничних" функцій розподілу: максимальну функцію розподілу отримуємо, обираючи з кожної групи необхідну кількість ввімкнених найпотужніших машин, а мінімальну – найменш потужних. Для обох переліків ввімкнених машин виконується точний розрахунок струмів і напруг усіх гілок мережі [4], результати цих розрахунків дають абсциси максимальної та мінімальної функцій розподілу відповідно. Паралельно з розрахунком, накопичується сума ймовірностей варіантів, що розглядаються, і коли вона досягає значення 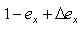, розрахунок припиняється. За отриманими значеннями ймовірностей ступенів та відповідними їм значеннями пікових струмів та втрат напруг формуються "граничні" (максимальна і мінімальна) функції розподілу цих величин та визначаються максимальні розрахункові значення. Цей алгоритм отримав назву метода "Граничних функцій розподілу" (ГФР).
Для ілюстрації в якості приклада будемо розглядати застосування всіх методів для розрахунку втрати лінійної напруги АВ в цеховій електричній мережі напругою 380 В на головній ділянці розгалуженого шинопровода, від якого отримують живлення 55 одно-, двох- та трифазних МКЗ різної потужності (від 20 до 495 кВА). Головна ділянка шинопровода ШМА 4 (номінальний струм 1250 А) довжиною 50 м підключена до трансформатора типу ТСЗ -1000/10. На рис. 1, (а, б, в) представлені максимальна (крива 1) та мінімальна (крива 2) граничні функції розподілу втрати напруги та максимальні розрахункові значення, визначені з граничною ймовірністю 
: 
- за максимальною, 
- за мінімальною функціями розподілу.
Очевидно, такий підхід дає малоймовірні граничні функції розподілу, однак він дозволяє чітко визначити межі, за які ніколи не вийдуть фактичні функції розподілу та максимальні розрахункові значення, визначені за ними. Щодо вибору мережі електропостачання, її неможливо обрати за втратами напруги, визначеними за мінімальною функцією розподілу і недоцільно обирати по втратам напруги, розрахованим за максимальною функцією розподілу. Тому метод "Граничних функцій розподілу" був вдосконалений: замість вибору з групи найпотужніших машин та машин найменшої потужності при розрахунку кожної сходинки максимальних та мінімальних функцій розподілу, що відповідає варіанту одночасного ввімкнення певних кількостей МКЗ з груп, ввімкнені машини з кожної групи обираються випадково. Цей метод отримав назву "Випадкового вибору" (ВВ). Але, як показали розрахунки, і він не може бути прийнятий за найточнішій, оскільки при багатократних розрахунках для тих самих вихідних даних отримуємо різні функції розподілу (група з 60 кривих 3 на рис. 1).
Наступним кроком покращення алгоритму став метод "Багатократного випадкового вибору" (БВВ), згідно з яким, при розрахунку кожної сходинки функцій розподілу виконується випадковий вибір ввімкнутих МКЗ багатократно, а отримані в результаті значення абсцис функцій розподілу осереднюються.
На рис. 1, б криві 4 – функції розподілу (15 кривих), отримані шляхом усереднення від 16 до 30 функцій розподілу за методом ВВ, а на рис. 1, в криві 5 – функції розподілу, отримані при кількості 
усереднених функцій розподілу від 46 до 60 (15 кривих). Збіг осереднених за методом БВВ функцій розподілу при 
дає підстави вважати рішення, отримане за ним, найбільш обґрунтованим з відомих методів розрахунку. На рис. 1, г представлена залежність (крива 6) максимального розрахункового значення втрати напруги, отриманого методом БВВ, від кількості усереднених функцій розподілу. При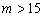 
воно вже майже не змінюється, значить для отримання достовірного результату в методі БВВ орієнтовно можна обмежитись 15-20 усередненнями.
Ординати горизонтальних ліній 7, 8 на рис. 1, г відповідають максимальним розрахунковим значенням втрати лінійної напруги, визначеним за максимальною та мінімальною функціями розподілу. Керівні вказівки та їх попередня редакція дають майже однакові результати: ордината точки 9 дорівнює втратам напруги, розрахованим за діючими Керівними вказівками, а точки 10 – за Керівними вказівками 1974 р. Якщо виконувати розрахунок за діючим Керівними вказівками, ця мережа не проходить за втратами напруги (припустима втрата напруги складає 10 % [2] ) навіть на головній ділянці шинопроводу. Через таке завищення розрахункових значень втрати напруги діючими Вказівками необхідно збільшити капітальні витрат на мережу, обравши трансформатор більшої потужності і (або) шинопровід більшого перетину.
Аналогічні результати були отримані і при розгляді функцій розподілу пікових струмів.
Рисунок 1 – Ділянки функцій розподілу втрати лінійної напруги АВ в мережі живлення групи МКЗ, визначені методами ГФР, ВВ, БВВ та її максимальні розрахункові значення.
Запропонований метод "Багатократного випадкового вибору" базується на точному розрахунку струмів і напруг мережі живлення машин контактної зварки та приблизному визначенні функцій розподілу пікових струмів і втрат напруги у мережі. Збіг осереднених функцій розподілу, отриманих методом БВВ при збільшенні кількості функцій розподілу, що осереднюються, дає підстави вважати метод БВВ достатньо обґрунтованим. Застосування метода БВВ забезпечить зменшення вартості електричних мереж живлення МКЗ. Застосований підхід до визначення функції розподілу може бути використаний в інших задачах, наприклад, при оцінці елект-ромагнітної сумісності за іншими показниками.
1. Вагин Г.Я. Режимы электросварочных машин / Г.Я. Вагин. – М.: Энергоатомиздат, 1985.- 192 с.