МОДЕЛИРОВАНИЕ ФУНКЦИОНИРОВАНИЯ ДУГОВЫХ СТАЛЕПЛАВИЛЬНЫХ ПЕЧЕЙ НА ОСНОВАНИИ ПРИМЕНЕНИЯ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ

Липецкий государственный технический университет

А.Н. Шпиганович, Ю.А. Шурыгин

В статье проведено моделирование функционирования дуговых сталеплавильных печей на основании применения искусственных нейронных сетей. Используя представленный алгоритм, можно решать важнейшие эксплуатационные задачи. Моделирование функционирования ДСП на основании применения ИНС позволяет получать и прогнозировать электрические параметры ДСП, которые невозможно измерить и тяжело получить расчетным путем.

Многие процессы, происходящие во время функционирования ДСП, имеют вероятностный характер и тяжело поддаются математическому описанию. Для создания достоверных моделей недостаточно иметь только математические зависимости электрических параметров электропечной установки. В настоящее время для моделирования режимов прогнозирования параметров электрической сети с дуговыми сталеплавильными печами (ДСП) все большее применение получают искусственные нейронные сети (ИНС). Это объясняется развитием методов искусственного интеллекта для оптимизации расхода энергоресурсов, используемых в процессе плавления металла. Главной задачей является ускорение процессов плавки за счет оптимального управления вводимой мощностью. Таким образом повышается эффективность совместной работы системы электроснабжения и ДСП. Особенность управления электрическим режимом ДСП заключается в частичном отсутствии изначальных знаний об этом объекте.

Широкое распространение получили методы «стадийного» управления. Такие методы основываются на четком определении границ стадий. На основании этого выбирается ступень напряжения трансформатора, а также задаются соответствующие команды регулятору. При применении статических методов границы стадий определяются на основании величины расхода электроэнергии, значения которой задаются на основании опытных или расчетных данных. Использование динамических методов основано на выявлении конкретной ситуации в печи с использованием измерений. «Стадийные» методы управления базируются на предположении о неизменности условий протекания стадий. На практике ситуация выглядит по-другому. Электрические показатели печи динамично изменяются в течение каждого цикла, и идентичных нагрузок в периоды каждой стадии не наблюдается. Это является недостатком «стадийного» управления.

Дуговая сталеплавильная печь может быть представлена в виде объекта с неустановленными взаимосвязями, который подвергается случайным воздействиям. Известными являются входные и выходные параметры. Для обеспечения оптимального поведения объекта система управления в процессе функционирования должна определить закон управления. Решить такую задачу можно за счет применения ИНС, позволяющих производить динамическое моделирование, реализуемое в виде обучения, идентификации и прогнозирования. Идентификация объекта управления производится с целью создания модели, функционирующей идентично исследуемому объекту. Схема идентификации представлена на рис. 1.

Рис. 1. Идентификация объекта

Она представляет собой схему прямого контролируемого обучения. Объект управления выступает в роли обучающего элемента, так называемого «учителя». Он содержит знания, которые представлены в виде входных и выходных значений величин. Для обучения необходимо большое количество таких данных, т.к. изначально ИНС не обладает никакой информацией. Во время обучения «учитель» постоянно взаимодействует с сетью, поступают входные тренировочные сигналы x, в качестве которых выступают значения напряжений ^ и токов I. Объект управления передает сети информацию, содержащую правильную реакцию на поступившее воздействие, и выдает выходное значение величины у. Обычно это мощность печного агрегата Р, мощность дуги Р_ди т.п. В результате возникает некоторая ошибка между реальными и желаемыми выходами сети. На основании этих данных производится настройка ИНС. Многократное повторение такого процесса обеспечивает обучение ИНС. Важной задачей является минимизации ошибки, заключающейся в разнице выходного сигнала от учителя и от модели.Чем больше количество образцов входных и выходных данных, тем меньше величина ошибки. Достоверность обучающих образцов носит определяющее значение. Ошибочные данные приводят к неправильному обучению ИНС. Величина ошибки также зависит от количества слоев, числа нейронов в каждом слое, вида активацион-ной функции, сложности связи между нейронами. Важным является установление компромиссного решения между скоростью обучения ИНС и величиной ошибки. При возмущении модель выдает выходные величины быстрее, чем реальная система, позволяя производить прогнозирование искомой величины. Это является существенным преимуществом таких моделей.

На основании вышеизложенного можно составить алгоритм построения ИНС под решение определенной задачи:

- определение схемы ИНС (число входов, количество слоёв и число нейронов в каждом слое);

- обучение ИНС;

- прогнозирование искомой величины и сравнение результатов.

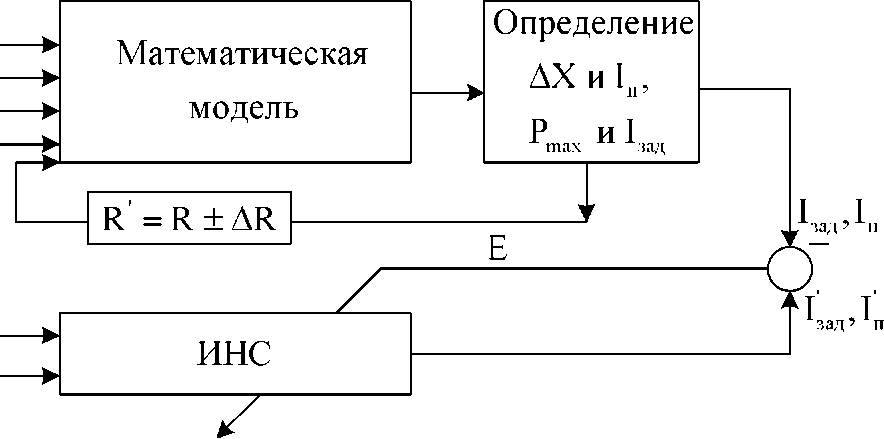
Обучение можно производить не только на основании статистических данных, полученных опытным путем, но и более простым способом, заключающимся в математическом описании электрических величин. К основным электротехническим особенностям ДСП относятся: несимметрия сопротивлений короткой сети, невозможность измерения длины и напряжения дуг, нелинейность нагрузки. Прогнозирование и регулирование этих параметров является важной эксплуатационной задачей. На практике возникает задача оптимизации активной мощности Р или мощности, выделяемой в дуге Р_д. В этом случае необходимо определить управляющее воздействие, вызывающее перемещение электрода к положению, которому соответствует оптимальное выделение мощности дуги при определенном значении длины и сопротивлении дуги. Необходимо учитывать влияние излучения дуги на футеровку стен и свода. Минимизировать несимметрию токов и напряжения в короткой сети возможно за счет регулирования реактивного сопротивления управляемого реактора, включаемого во вторичную цепь печного трансформатора. В качестве «учителя» целесообразно использовать математическую модель, представленную в [3]. Схема ИНС для этого случая представлена на рис 2.

Рис. 2. Схема ИНС

Помимо определения мощностей Р и Р_д перед математической моделью стоит задача определения такого сопротивления дуги К, соответствующего её максимальной мощности. Затем производится вычисление реактивного сопротивление каждого токопровода короткой сети. На основании сравнения значений реактивных сопротивлений АX определяется ток подмагничи-вания обмотки управления 1_п для каждой из фаз. Величина тока при сопротивлении дуги К будет являться искомой величиной для определения задания регулятору (гидравлическому приводу). При любых изменениях напряжения необходима коррекция уставки. Так производится управление режимами функционирования ДСП. Для моделирования функционирования дуговой сталеплавильной печи на основании нейронной сети рекомендуется использовать пакет программы МаtLab 7.7 Simukink.

Используя представленный алгоритм, можно решать важнейшие эксплуатационные задачи. Моделирование функционирования ДСП на основании применения ИНС позволяет получать и прогнозировать электрические параметры ДСП, которые невозможно измерить и тяжело получить расчетным путем.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Бош, В.И. Особенности систем электроснабжения сталеплавильных производств [Текст]: монография / В.И. Бош, Е.П. Зацепин. - Липецк: ЛГТУ, 2006. - 152 с.

2.Лапшин, И.В. Автоматизация дуговых печей [Текст] / И.В. Лапшин. - М.: Энергия, 2004. - 166 с.

3.Шпиганович, А.Н. Регулирование электрических параметров дуговых сталеплавильных печей с использованием управляемых реакторов [Текст] / А.Н.

Шпиганович, Е.П. Зацепин, Ю. А. Шуры-гин // Вести высших учебных заведений Черноземья. - 2009. - № 1.