Математическая модель для определения напряжения и тока с учётом потерь в линиях электропередачи

 

М.О. Оке

Факультет электротехники и электронной техники

Государственный университет Экити

Адо-Экити, Нигерия

Автор перевода: Шевченко А.В.

Аннотация: энергия является основной необходимостью для экономического развития страны. Существуют различные формы энергии, но наиболее важной формой является электрическая энергия. В современном и цивилизованном обществе так много зависит от использования электрической энергии. Электрическая энергия передается с помощью линий, которые доставляют огромные мощности от генерирующих станций до центров нагрузки. Промышленное развитие любой страны зависит от надежности ее взаимосвязанной электроэнергетической системы. Наличие электрической энергии есть самым мощным средством для содействия экономическому, промышленному и социальному развитию любого государства. Когда электроэнергия вырабатывается в достаточном количестве, она должна быть передана в узлы нагрузки где затем распределяется по отдельным потребителям в надлежащей форме при минимально возможных экологических и экономических потерях. Эта электрическая мощность передается посредством линий электропередачи. В данной работе мы разработали математические модели для определения напряжения и тока с учётом потерь в линиях электропередач. Мы получили отношения напряжение, которое удовлетворяет общепринятым условиям качества электроэнергии. Модели содержат первичные константы и параметры линии передачи, которые включают в себя сопротивление (R), шунт проводимости (G), индуктивность (L) и емкость (C). Значения этих констант определяются на единицу длины.

Ключевые слова: уравнения линии электропередач, математическая модель, потери передачи, утечки в линиях электропередач, параметры передачи.

 

I. ВВЕДЕНИЕ

Социальные структуры и промышленное развития любой страны зависит в первую очередь от низкой стоимости и бесперебойного электроснабжение. Процесс модернизации, повышения производительности труда, сельского хозяйства и промышленности в основном зависят от достаточного снабжения электрической энергией.

Генерация электрической энергии является преобразованием энергии доступной в различных формах в природе в электрическую энергию. От постоянно увеличивающегося использования электрической энергии в промышленных, бытовых и коммерческих целях, необходимость массового производства электрической энергии возросла. Это массовое производство достигается с помощью соответствующей мощности производства станций, которые обычно называют электроэнергетические станции или электростанции. В генераторной электростанции обычно используют первичный двигатель в сочетании с генератором для выработки электроэнергии. Электрическая энергия вырабатывается на электростанциях, которые обычно расположены далеко от центров нагрузки. Поэтому требуются обширные системы электроснабжения между электростанциями и потребителями. Эти системы могут быть разделены на два основных компонента, называемые системами передачи и распределения. Система электроснабжения необходима для доставки огромной мощности от электростанции к центрам нагрузки и крупным промышленным потребителям в то время, как система распределения необходима для передачи мощности от ПС до различных потребителей. Электрическая энергия должна передаваться и распределяться к месту использования как только это необходимо. Для достижения этой цели необходимы линии электропередач. Линии электропередач представляют собой системы энергетического оборудования, которые используются для передачи электрической энергии и сигналов от одной точки к другой, в частности, от источника к нагрузке. Их можно рассматривать как набор проводников, идущих из одного места в другое. Они включают в себя связь между генераторной установкой и подстанцией, что в нескольких сотен километров. Этапы передачи и распределение очень важны для электроэнергетической системы, потому что без этих этапов генерируемая мощность не может добраться до центров нагрузки, не говоря уже о получении её конечным потребителем.

 

II. МОТИВАЦИЯ К ИЗУЧЕНИЮ

Многие научно-исследовательской работы были проведены учеными и инженерами по генерации мощности, надежности систем передачи и снижения потерь на линиях: Bamigbola (2009) рассмотрел характеристику оптимальной модели управления электроэнергетических систем с использованием двух переменных управления, Aderinto (2010) разработал математическую модель для электроэнергетических систем с помощью оптимального подхода управления с одной управляющей переменной, Okafor (2009) оценил надежность передачи системы в Нигерии с помощью общей функции надежности и вычисления показателей надежности в шести линий электропередачи 330 кВ в Нигерии. Bagriyanik (2003) использовал нечеткую многоцелевую оптимизацию и генетический алгоритм на основе метода, чтобы найти оптимальные условия энергосистемы. В дополнение к потерям активной мощности, серия реактивных потерь мощности передаваемой системой, также рассматриваются как одна из нескольких задач. Onohaebi (2010) рассмотрела взаимосвязь влияния расстояния и нагрузки на потери мощности при использовании существующих линий 330 кВ в качестве примера своей эмпирической модели потерь мощности в зависимости от нагрузки и длинны линии электропередач. Математические модели для определения напряжения и тока на линиях с потерями электроэнергии передачи не было представлено в работах этих исследователей, следовательно, необходимость в данной работе возросла. В этой статье мы представляем математические модели для определения напряжения и тока с учётом потерь в линиях в форме частных производных дифференциальных уравнений второго порядка.

Было получено соотношение напряжении и тока для линии электропередач. Мы построили модель схемы для дополнительных длин линии и написали две системы уравнений, которые в настоящее время используются для получения дифференциального уравнения. Реальная модель передачи будет иметь некоторое последовательное сопротивление, связаное с потерями в проводнике. Там также может быть некоторый шунт проводимости, если изоляционный материал имеет некоторый ток утечки. Таким образом, сопротивление и проводимость ответственны за потери мощности при передаче. Поэтому они очень важны, когда эффективность передачи и экономика должны быть важны. С этой целью, мы формулируем модель для линии передачи с потерями, где появляется эффект последовательного сопротивления (R) и шунтирующих проводимостей (G).

 

III. РАЗРАБОТКА МОДЕЛЕЙ

 В этой работе, мы заинтересованы в определении степени, в которой выходное напряжение и ток отличается от своих входных значений, так как длина линии передачи приближается к очень малой величины. С этой целью рассмотрим эквивалентную схему линии передачи, содержащей сопротивления R, емкости C индуктивности L и проводимости G, как показано на рисунке ниже:

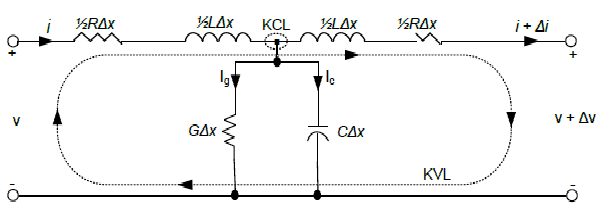
Рисунок 3.1 Схема замещения линии передачи.

 

На рисунке выше представлена симметричная сеть, поэтому мы разделим её элементы на два. Используя Закон Кирхгофа мы получим:

Разделив уравнение (3.1) на 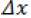и упростив, мы получим:

Принимая придел , получим:

Применив действующий Закон Кирхгофа на эквивалентную схему линии передачи, имеем:

Т.е.

Разделив уравнение (3.5) на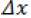 и упростив, мы получим:

Принимая придел , получим:

Дифференциальные уравнения (3.3) и (3.7) описывают изменение тока и напряжения в линиях передачи с учётом потерь.

Дифференцируя уравнение (3.3) по х у нас есть

и дифференцируя уравнение (3.7) относительно t, мы имеем

Подставляя (3.7) и (3.9) в (3.8), имеем

Дифференцируя уравнение (3.3) относительно t имеем

и дифференцируя уравнение (3.7) относительно х, мы имеем

Подставляя (3.3) и (3.11) в (3.12), имеем

Уравнения (3.10) и (3.13) являються гиперболическими дифференциальными уравнениями, которые описывают напряжения и ток вдоль линий электропередачи.

 

IV. ЗАКЛЮЧЕНИЕ

 Мы получили частные производные первого порядка дифференциальных уравнений, которые показывают изменение напряжения и тока по линиям электропередачи за счет использования законов Кирхгофа. Частные производные второго порядка дифференциальных уравнений, которые описывают изменение напряжения и тока вдоль линии электропередач были также получены в данной работе.