Э.Д. Ешелева, А.К. Пронина, К.П. Путилин - МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ НЕСИММЕТРИЧНЫХ РЕЖИМОВ ЭЛЕКТРИЧЕСКОЙ СИСТЕМЫ

УДК 621.3.077:519.97

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ НЕСИММЕТРИЧНЫХ РЕЖИМОВ ЭЛЕКТРИЧЕСКОЙ СИСТЕМЫ

Э.Д. Ешелева, К.П. Путилин (Севастопольский национальный университет ядерной энергии и промышленности),
А.К. Пронина (Севастопольский национальный технический университет)

Оценивается симметрирующая роль синхронных машин, работающих в режиме двигателя или компенсатора. Разработанная математическая модель позволяет получить количественную оценку эффективности симметрирования.

1. Введение

Актуальность темы обусловлена ухудшением качества электрической энергии в современных промышленных сетях из–за увеличения числа и мощности однофазных потребителей. Возникающая при этом несимметрия трехфазных сетей резко отрицательно сказывается на работе трехфазных потребителей, приводит к увеличению дополнительных потерь в линиях, трансформаторах, ухудшая экономические показатели работы сетей.

Научные и практические задачи симметрирования приобретают важное значение для улучшения технико-экономических показателей работы современных сетей.

Известные пути решения задач симметрирования базируются, главным образом, на построении реактивной компенсации на основании схем Штейнмеца и сопряжены с большими технико–материальными затратами.

В то же время существует метод компенсации реактивных симметричных мощностей с помощью синхронных компенсаторов. При этом на местном уровне синхронные компенсаторы традиционно заменяются статическими конденсаторными батареями.

В предыдущих работах рассматривались потери в несимметричных трехфазных сетях [1, 2].

Разработанное математическое моделирование позволяет оценить количественный эффект симметрирования в синхронной машине, которая используется в качестве компенсатора реактивной мощности.

Постановка цели и задачи научного исследования

Цель научного исследования – разработать математическую модель для оценки качества электрической энергии по показателю несимметрии при использовании синхронного компенсатора или синхронного двигателя для симметрирования сетей потребления.

Для достижения поставленной цели необходимо проанализировать несимметричный режим трехфазной системы и возможные способы симметрирования при включении в состав электрической системы синхронных машин.

Анализ несимметричного режима трехфазной системы

Крупные узлы потребления, обеспечиваемые электрической энергией переменного трехфазного тока через протяженные линии передачи, часто содержат значительные мощности однофазных потребителей, или несимметричную резко переменную нагрузку (типа дуговых сталеплавильных печей ДСП). В последнем случае симметрирование с помощью регулируемых статических индуктивно–емкостных устройств оказывается неэффективным, а часто и просто невозможным. При этом реактивные мощности компенсирующих устройств оказываются значительными, кроме того в них возможны опасные резонансные явления, так как в кривой напряжения могут оказаться высшие гармонические. Одновременно, крупные узлы потребления могут иметь в своем составе вспомогательные генераторные станции, синхронные машины в качестве двигателей или компенсаторов.

Приводимый ниже анализ показывает, что синхронная машина может выполнять функции симметрирующего устройства одновременно со своим основным назначением. Результатом такого симметрирования будет уменьшение потерь энергии в основной линии снабжения при достаточном ее протяжении. Кроме того, на шинах потребителей возможно уменьшение до нормы коэффициента напряжения обратной последовательности, то есть улучшение качества электрической энергии. Степень улучшения определяется расчетом, производимым на основе математической модели.

Принципиальная схема моделируемой системы дана на рис. 1.

Рис.1

На рис. 1 основным источником питания несимметричного трехфазного потребителя, подключенного к шинам Ш узла нагрузки, служит удаленная мощная станция 1. Вблизи узла нагрузки к шинам Шподключена синхронная машина 2.

Разработка математической модели

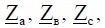Схема замещения моделируемой системы приведена на рис. 2, где несимметричный потребитель представлен сопротивлениями article5_pic2

причем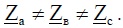

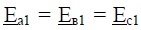Основная линия питания включает симметричный ЭДС article5_pic4

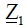за сопротивлением линии article5_pic5

, одинаковым для всех трех фаз.

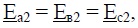Синхронная машина вблизи узла потребления представлена ЭДС article5_pic6

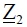за сопротивлением линии article5_pic7

. ЭДС и сопротивления на схеме показаны для прямой последовательности.

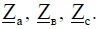Симметричные потребители шин Ш учтены в сопротивлениях article5_pic8

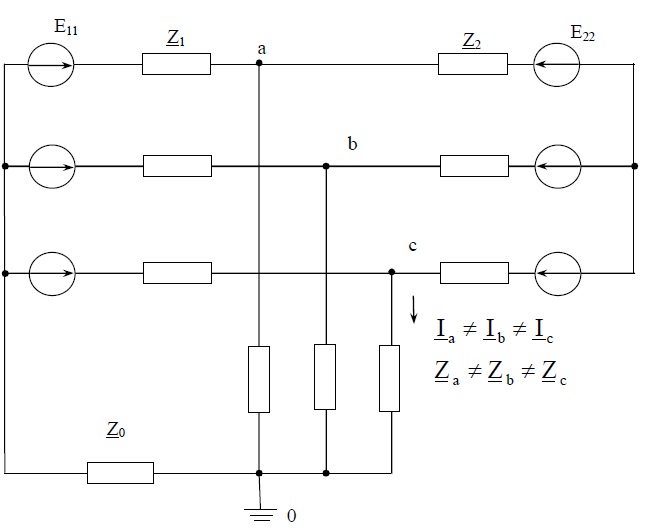
Рис.2

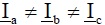Эквивалентная нагрузка при токах article5_pic10

определяет напряжения в точках a, b, c относительно нуля 0 следующим образом:

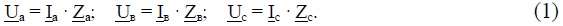
Через симметричные составляющие напряжения (1) могут быть записаны как

Эквивалентные схемы последовательностей напряжения и тока: прямой (а), обратной (б) и нулевой (в) изображены на рис. 3.

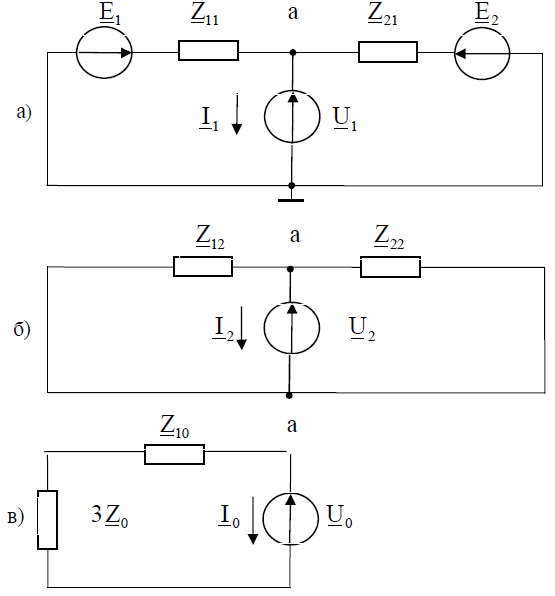
Рис.3

Через I₁, I₂ ,I₀ изображены симметричные составляющие токов в нагрузку.

По второму закону Кирхгофа для схем последовательностей запишем

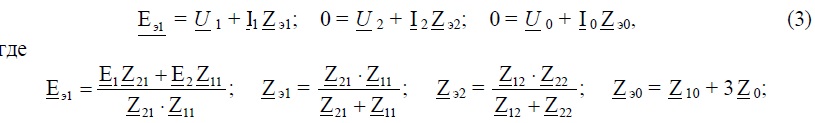
В трех уравнениях (3) неизвестными являются величины I₁, I₂ ,I₀ и U₁, U₂ ,U₀.
Дополнительные три уравнения составим, учтя равенства (1), в которых фазные величины напряжения и тока в точках a, b, c их симметричными составляющими:

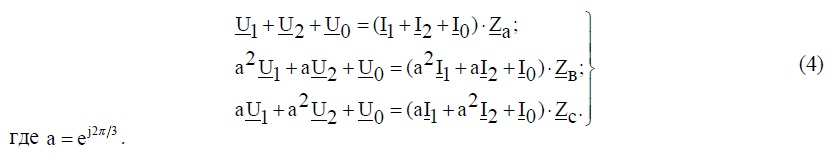
Из решения системы уравнений (3), (4), находим неизвестные составляющие напряжения и тока прямой (индекс 1), обратной (индекс 2) и прямой (индекс 0) последовательностей. Таким образом, данная система уравнений полностью определяет несимметричный режим системы, то есть представляет ее математическую модель.
Распределение токов последовательностей осуществляется по их схемам замещения рис 3, а, б, в.
Используя подстановки, задачу можно упростить, сведя систему уравнений модели к трем уравнения вместо шести:

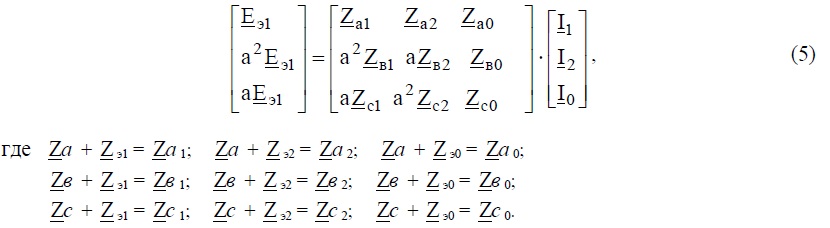
Решение уравнений (5) по формулам Крамера

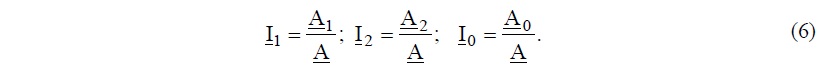
где A – определитель матрицы сопротивлений (5), I₁, I₂ ,I₀ - определители, если в матрице сопротивлений столбцы первый, второй и третий заменять, соответственно, элементами столбцовой матрицы ЭДС (слева в (5)).
По известным токам I₁, I₂ ,I₀(6) находятся напряжения последовательностей

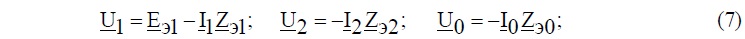
и коэффициент обратной и первой последовательности для напряжения

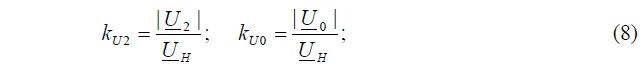
Для сравнения эти коэффициенты определяются при отсутствии источника Е₂ и при его включении в схему.
Для оценки потерь в линии и их изменения за счет уменьшения токов обратной последовательности можно воспользоваться методикой, представленной в [2]:

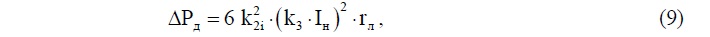
Где К_2і=I₂/I_н – коэффициент тока обратной последовательности по ГОСТ 13109 – 97;
К_з – коэффициент загрузки линии по току;
1_л – активное сопротивление фазы, включающее сопротивление линейного провода и фазы трансформаторов в линии.
Для построения схемы замещения должны быть использованы параметры реальных схем, изменяя которые, можно решать задачи оценки фактических дополнительных потерь и их уменьшения.

Выводы

Разработана математическая модель для оценки качества электрической энергии по показателю несимметрии при использовании синхронного компенсатора или синхронного двигателя для симметрирования сетей потребления.

Дальнейшие исследования в данном направлении заключаются в экспериментальных исследованиях для проверки адекватности разработанной математической модели и оценки ее эффективности. Результаты исследований могут быть использованы в процессе проектирования промышленных сетей или их модернизации.

Список использованных источников

1. Бурбеко М.И. Анализ условий симметирирования нагрузок с использованием компенсационных симметрирующих установок / М.И. Бурбеко // Энергетика и электрификация. – К., 2009. – № 5. – С. 3 – 6.

2. Ешелева Э.Д. Расчет добавочных потерь в трансформаторах по коэффициенту несимметрии / Э.Д. Ешелева, К.П. Путилин // Зб. наук. пр.СНУЯЕтаП. – Севастополь:СНУЯЭиП, 2009. – Вып. 2 (30). – С. 197 – 203.