Анотація
Розглянуто рух одиночного екіпажу впродовж підвісної монорейки, секції якої шарнірно з'єднані між собою і мають перевищення у стиках. Розроблено математичну модель вертикальних коливань, яка представлена у вигляді двомасової системи. Модель враховує коливання ходового колеса на пружній монорейці та коливання підвісної частини екіпажу. В результаті встановлено, що коливання екіпажу визначаються станом всієї системи. Однак коливальний процес колеса практично не залежить від параметрів підвісної частини екіпажу.
Ключові слова
підвісна монорейкова дорога, екіпаж, динамічне навантаження, деформація, математична модель
Постановка проблеми
Під час руху екіпажу по підвісному монорейковому шляху завдяки нерівностям ходових коліс і монорейки неминуче виникають збурення, які мають ймовірнісний характер. Збурення виникають внаслідок пружних деформацій, які відбуваються під час руху. Змінюючись у просторі та часі змінні навантаження виникають у місцях контакту ходових коліс з монорейкою.
Крім того, монорейка має з’єднання, які допускають зазори та різні відхилення. Всі ці фактори викликають додаткові динамічні навантаження на кріплення гірничої виробки, що зменшує її міцність. Саме вирішення цієї проблеми шляхом дослідження взаємозв’язку ходового колеса з монорейкою є актуальним питанням.
Аналіз останніх досліджень і публікацій
Вітчизняні та зарубіжні вчені виконали ряд робіт [1, 2, 3, 4], які присвячені дослідженню динамічних процесів, що відбуваються у системі «колесо-рейка» зокрема в зоні рейкового стику.
Постановка задачі
Дана робота є продовженням зазначених досліджень. Мета статті полягає у встановленні взаємозв’язку між параметрами екіпажу і підвісної монорейки, яка має перевищення у стиках.
Матеріали та результати досліджень
Під час руху одиночного екіпажу по стикам підвісної монорейки, секції якої з’єднуються між собою та мають зазори  (рис.1), виникають імпульсні удари зумовлені змінами напрямку руху швидкості центра мас ходового колеса. Ці удари призводять до коливань не підресорених мас, передаються екіпажу підвісної монорейкової дороги та кріпленню гірничої виробки.
(рис.1), виникають імпульсні удари зумовлені змінами напрямку руху швидкості центра мас ходового колеса. Ці удари призводять до коливань не підресорених мас, передаються екіпажу підвісної монорейкової дороги та кріпленню гірничої виробки.
Розглянемо модель вертикальних коливань, яка представлена у вигляді двомасової системи, яка враховує коливання ходового колеса на пружній монорейці, а також коливання підвісної частини екіпажу. Введемо наступні позначення:  – приведена маса ходових коліс;
– приведена маса ходових коліс; 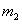 – приведена маса підвісної частини екіпажу;
– приведена маса підвісної частини екіпажу; 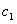 – жорсткість монорейки на стику;
– жорсткість монорейки на стику; 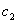 – жорсткість підвіски екіпажу;
– жорсткість підвіски екіпажу; 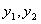 – узагальнені координати переміщення центрів мас ходових коліс і підвісної частини екіпажу, відповідно.
– узагальнені координати переміщення центрів мас ходових коліс і підвісної частини екіпажу, відповідно.
Сила, яка діє на дану систему – це миттєвий імпульс, який виникає при переміщенні ходових коліс через стики монорейки:
 (1)
(1)

Рисунок 1 – Схема руху екіпажу по стиках підвісної монорейки
Кінетичну енергію системи у даному випадку можна записати як
 (2)
(2)
Потенціальну енергію визначимо як суму потенціальної енергії відповідної сили пружності підвіски екіпажу і потенціальної енергії відповідної сили пружності монорейки:
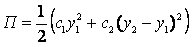 (3)
(3)
Запишемо рівняння Лагранжа у вигляді:
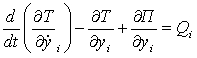 (4)
(4)
де 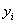 – узагальнені координати;
– узагальнені координати;
 – узагальнені зовнішні сили.
– узагальнені зовнішні сили.
З рівнянь (1), (2), (3) та їх похідних для рівняння Лагранжа отримаємо:
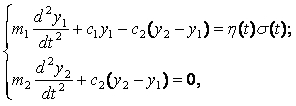 (5)
(5)
де  – імпульсивна функція першого порядку.
– імпульсивна функція першого порядку.
Для розв’язання рівняння (5) введемо наступні позначення:
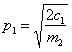 ,
,  ,
, 
де 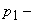 власна частота коливань підвісної частини екіпажу.
власна частота коливань підвісної частини екіпажу.
Розв’яжемо рівняння (5) за допомогою операційного методу. Для цього позначимо зображення початкових функцій:
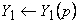
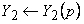
Запишемо систему диференційних рівнянь при нульових початкових умовах:

Розв’язавши рівняння отримаємо:
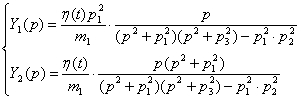
Повернувшись від зображень функцій до оригіналів запишемо:
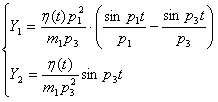 (6)
(6)
Проаналізувавши систему (6), можливо сказати, що коливання екіпажу залежать від стану всієї системи. Але коливальний процес колеса практично не залежить від параметрів підвісної частини екіпажу. Тому при проведенні досліджень руху по стиках монорейки можливо не враховувати коливання підвісної частини. Тоді функцію, яка описує імпульсні впливи на стиках монорейки можна записати як

На рис. 2 показані графіки залежності цієї функції в часі, побудовані для наступних значень вхідних параметрів:  5х10^4 Н*с;
5х10^4 Н*с; 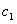 =5х10^6 Н/м^2;
=5х10^6 Н/м^2; 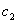 =2х10^6 Н/м2;
=2х10^6 Н/м2;  =200 кг.
=200 кг.
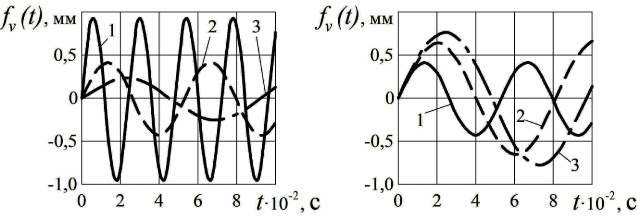
Рисунок 2 – Графіки залежності функції  у часі:
у часі:
а – для 1 –  = 500 кг; 2 – 1000 кг; 3 – 3000 кг;
= 500 кг; 2 – 1000 кг; 3 – 3000 кг;
б – для 1 – 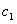 = 5,0*10^6 Н/м^2; 2 – 1,0*10^6 Н/м^2; 3 – 0,1*10^6 Н/м^2
= 5,0*10^6 Н/м^2; 2 – 1,0*10^6 Н/м^2; 3 – 0,1*10^6 Н/м^2
Із рис. 2а видно, що зі збільшенням маси колеса амплітуда і частота функції  зменшується. Так для
зменшується. Так для  = 500 кг максимальна амплітуда коливань складає 0,9 мм, а при 3000 кг – 0,2 мм.
= 500 кг максимальна амплітуда коливань складає 0,9 мм, а при 3000 кг – 0,2 мм.
Як зазначено на рис. 2б, при зниженні жорсткості монорейки або підвісної части-ни екіпажу амплітуда і частота функції підвищуються. Причому, у разі зменшення 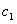 в 10 разів амплітуда
в 10 разів амплітуда  збільшується всього в 1,6 рази та складає не більше 0,75 мм.
збільшується всього в 1,6 рази та складає не більше 0,75 мм.
Висновки
Отримані залежності, які описують процес взаємодії екіпажу з підвісною монорейкою будуть використовуватися для обґрунтованого вибору параметрів шахтних підвісних монорейкових доріг. В подальшому планується провести теоретичні дослідження з урахуванням поздовжніх коливань монорейкового поїзда, обумовлених взаємодією підвісних екіпажів.
Перелік використаної літератури
1. Блохин Е. П. Динамика вагона / Е.П. Блохин, Л.А. Манашкин. – М.: Транспорт, 1982, – 222 с.
2. S. Hyun, M. O. Robbins: Elastic contact between rough surfaces: Effect of roughness at large and small wavelengths. Tribology International, 2007, v.40, pp. 1413–1422.
3. Мямлин С.В. Моделирование динамики рельсовых экипажей / С.В. Мямлин. – Днепропетровск: Новая идеология, 2002. – 240 с.
4. Шахтарь П.С. Рудничные локомотивы / П.С. Шахтарь. – М.: Недра, 1982. – 296 с.
5. Коган А. Я. Динамика пути и его взаимодействие с подвижным составом / А.Я. Коган. – M: Транспорт, 1997. – 326 с.
6. Горячева И.Г. Механика фрикционного взаимодействия / И.Г. Горячева. – М.: Наука, 2001. – 478 с.
7. Соколов M.М. Динамическая нагруженность вагона / М.М. Соколов, В.Д. Хусидов, Ю.Г. Минкин. – М.: Транспорт, 1981, – 207 с.
8. Бородин А. В. Как уменьшить удары колес в стыках / А. В. Бородин, В. В. Иванов // Путь и путевое хозяйство. 2008. № 6. – С. 13 - 14.
9. Богданов В.М. Моделирование процессов контактирования, изнашивания и накопления повреждений в сопряжении колесо – рельс / В.М. Богданов, А.П. Горячев, И.Г. Горячева и др. // Трение и износ. – 1996. – Т.17. – №1. – С.12–26.